A fire hydrant delivers water of density ρ at a volume rate L. The water travels vertically upward through the hydrant and then does 90∘ turn to emerge horizontally at speed V. The pipe and nozzle have uniform cross-seciton throughout. The force exerted by the water on the corner of the hydrant is

ρVL
zero
2ρVL
√2ρVL
The correct Answer is:D
Step by step video & image solution for A fire hydrant delivers water of density rho at a volume rate L. The water travels vertically upward through the hydrant and then does 90^@ turn to emerge horizontally at speed V. The pipe and nozzle have uniform cross-seciton throughout. The force exerted by the water on the corner of the hydrant is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - II
6 Videos
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - III
7 Videos
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (C)
5 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
A fire hydrant delivers water of density ρ at a volume are L. The water travels vertically upward through the hydrant and then does 90∘ turn to emerge horizontally at speed V. The pipe and nozzle have uniform cross-section through out. The force exerted by the water on the corner of the hydrant is
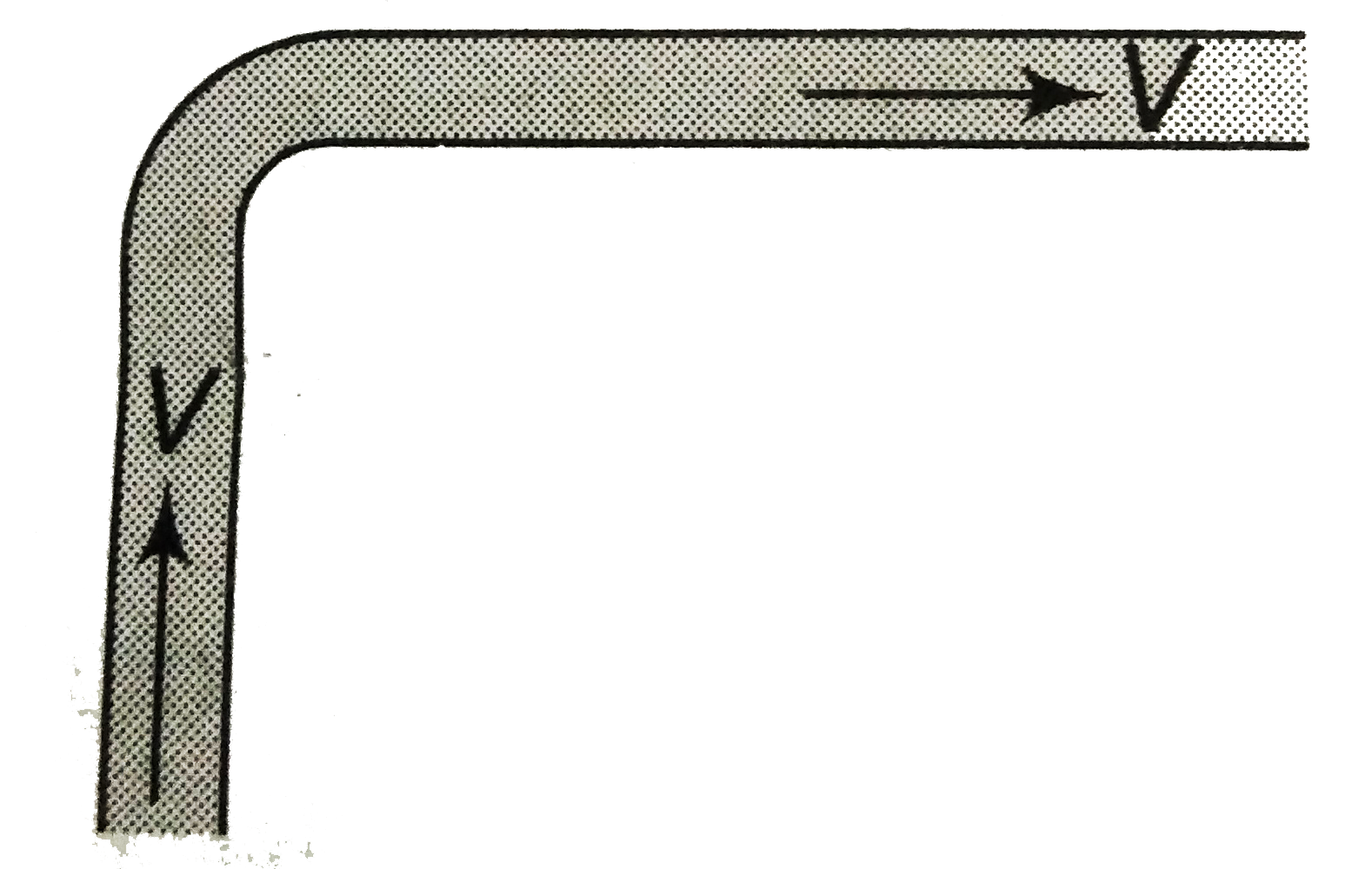
View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View Solution
Knowledge Check
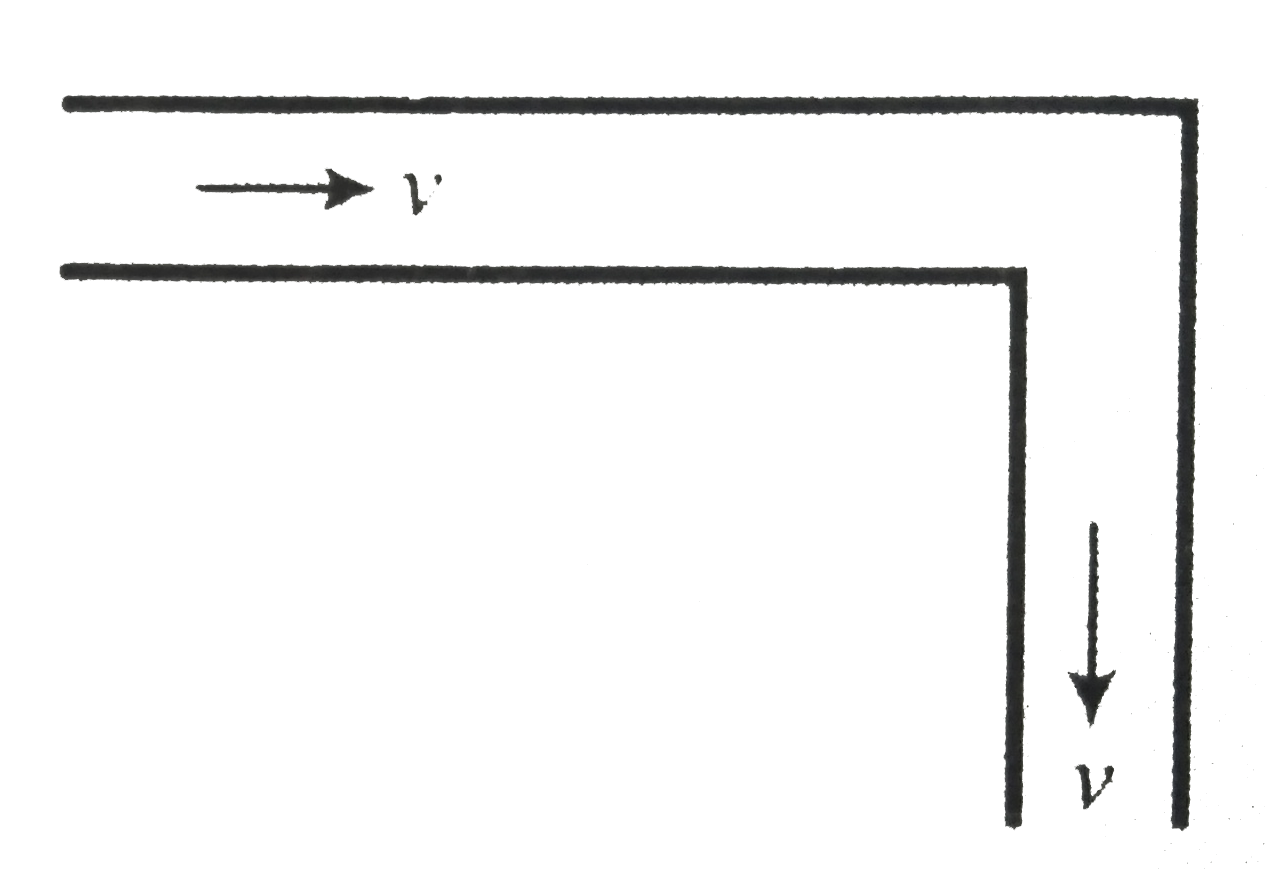
A liquid of density ρ flows along a horizontal pipe of uniform cross-section A with a velocity v through a right angled bend as shown in fig. What force has to be exerted at the bend to hold the pipe in equilibrium ? .
A2aρv2Baρv2/√2C√2aρv2Daρv2
A liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
View SolutionA plate moves normally with the speed v1 towads a horizontal jet of uniform area of cross-section. The jet discharge water at the rate of volume V per second at a speed of v2. The density of water is ρ. Assume that water splashes along the surface of the plate ar right angles to the original motion. The magnitude of the force action on the plate due to the jet of water is
View SolutionA plate moves normally with the speed v1 towads a horizontal jet of uniform area of cross-section. The jet discharge water at the rate of volume V per second at a speed of v2. The density of water is ρ. Assume that water splashes along the surface of the plate ar right angles to the original motion. The magnitude of the force action on the plate due to the jet of water is
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.
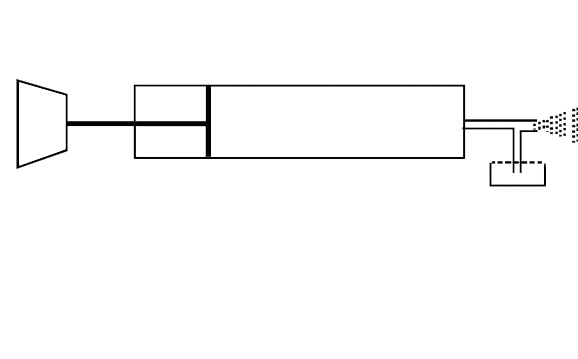
If the density of air is ρa, and that of the liquid ρl, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to
View SolutionLiquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of 0∘C, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions . It can lose energy and freeze only by sending energy up(through distance L) to the top of the icicle, where the temperature Tr can be below 0∘C. Take L=0.10m and Tr=−5∘C.Assume that the central tube and the upward conduction path both have crosse-sectional area A=0.5m2. The thermal conductivity of ice is 0.40 W/m⋅K, latent heat of fusion is LF=4.0×105J/K and the density of liquid water is 1000 kg/m3.
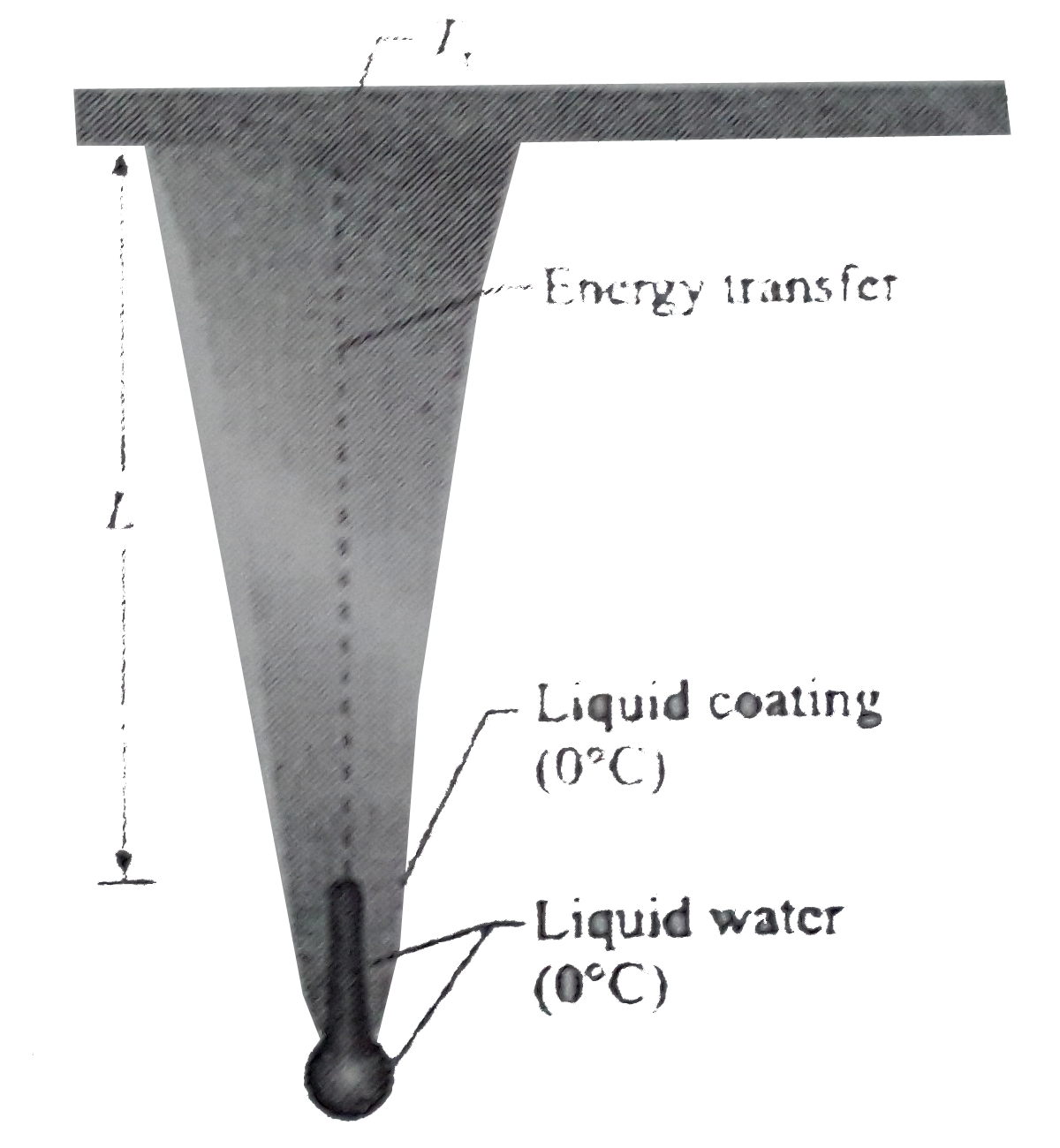
At what rate does the top of the tube move downward because of water freezing there?
View SolutionLiquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of 0∘C, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions . It can lose energy and freeze only by sending energy up(through distance L) to the top of the icicle, where the temperature Tr can be below 0∘C. Take L=0.10m and Tr=−5∘C.Assume that the central tube and the upward conduction path both have crosse-sectional area A=0.5m2. The thermal conductivity of ice is 0.40 W/m⋅K, latent heat of fusion is LF=4.0×105J/K and the density of liquid water is 1000 kg/m3.
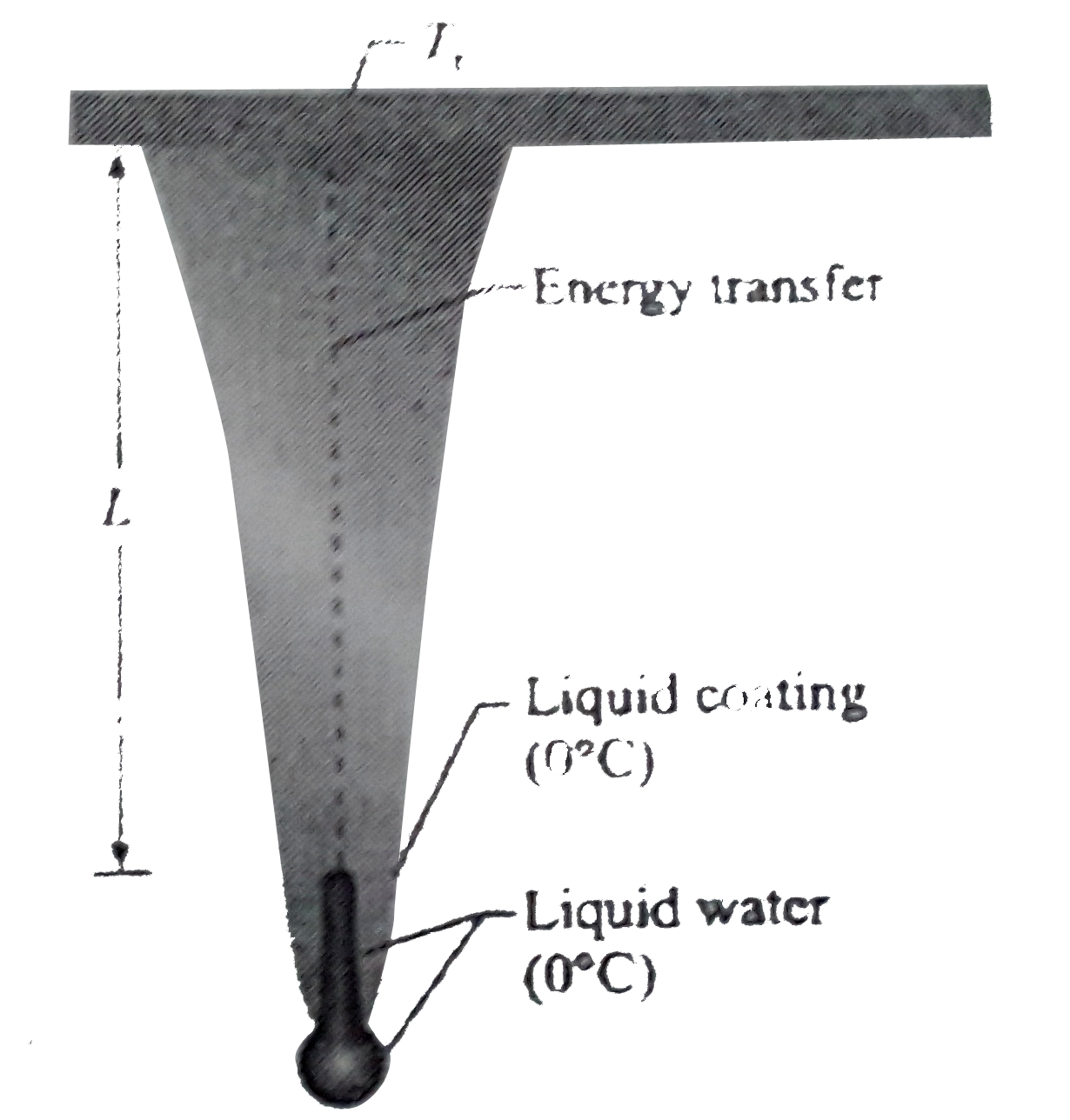
The rate at which mass converted from liquid to ice at the top of the central tube is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the Body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The density of the solid is
View Solution