A barometer contains two uniform capillries of radii 1.44×10−3m and 7.2×10−4m. If the height of the liquid in the narrow tube is 0.2m more than that in the wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=m/s2.
To solve the problem, we need to calculate the true pressure difference between the two capillaries in the barometer. The given data includes the radii of the capillaries, the height difference of the liquid columns, the density of the liquid, the surface tension, and the acceleration due to gravity.
1. Identify Given Values:
- Radius of narrow capillary, r1=1.44×10−3m
- Radius of wide capillary, r2=7.2×10−4m
- Height difference of liquid, h=0.2m
- Density of liquid, ρ=103kg/m3
- Surface tension, T=72×10−3N/m
- Acceleration due to gravity, g=9.8m/s2
2. Calculate the Hydrostatic Pressure Difference:
The pressure difference due to the height of the liquid column can be calculated using the formula:
ΔP=h⋅ρ⋅g
Substituting the values:
ΔP=0.2m⋅103kg/m3⋅9.8m/s2
ΔP=0.2⋅1000⋅9.8=1960N/m2
3. Calculate the Excess Pressure due to Surface Tension:
The excess pressure in a capillary tube is given by:
ΔPexcess=2T(1r1−1r2)
Substituting the values:
ΔPexcess=2⋅72×10−3(11.44×10−3−17.2×10−4)
First, calculate 1r1 and 1r2:
1r1=11.44×10−3≈694.44m−1
1r2=17.2×10−4≈1388.89m−1
Now, calculate the difference:
1r1−1r2=694.44−1388.89=−694.45m−1
Now substitute back into the excess pressure equation:
ΔPexcess=2⋅72×10−3⋅(−694.45)≈−100.00N/m2
4. Calculate the True Pressure Difference:
The true pressure difference is given by:
ΔPtrue=ΔP+ΔPexcess
Substituting the values:
ΔPtrue=1960+(−100)=1860N/m2
Final Answer:
The true pressure difference is 1860N/m2.
- Radius of narrow capillary, r1=1.44×10−3m
- Radius of wide capillary, r2=7.2×10−4m
- Height difference of liquid, h=0.2m
- Density of liquid, ρ=103kg/m3
- Surface tension, T=72×10−3N/m
- Acceleration due to gravity, g=9.8m/s2
The pressure difference due to the height of the liquid column can be calculated using the formula:
ΔP=h⋅ρ⋅g
Substituting the values:
ΔP=0.2m⋅103kg/m3⋅9.8m/s2
ΔP=0.2⋅1000⋅9.8=1960N/m2
The excess pressure in a capillary tube is given by:
ΔPexcess=2T(1r1−1r2)
Substituting the values:
ΔPexcess=2⋅72×10−3(11.44×10−3−17.2×10−4)
1r1=11.44×10−3≈694.44m−1
1r2=17.2×10−4≈1388.89m−1
1r1−1r2=694.44−1388.89=−694.45m−1
ΔPexcess=2⋅72×10−3⋅(−694.45)≈−100.00N/m2
The true pressure difference is given by:
ΔPtrue=ΔP+ΔPexcess
Substituting the values:
ΔPtrue=1960+(−100)=1860N/m2
The true pressure difference is 1860N/m2.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I10videos
SURFACE TENSION
- BOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II16videos
SURFACE TENSION
- BOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise27videos
UNITS, DIMENSION & MEASUREMENT
Similar Questions
A barometer contains two uniform capillaries of radii 1.4×10−3m and 7.2×10−4m. If the height of liquid in narrow tube is 0.2m more than that in wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=9.8ms−12.
View SolutionThe limbs of a manometer consists of uniform capillary tubes of radii 1.44×10−3m and 7.2×104m. If the level of the liquid in the narrower tube stands 0.2 m above that in the broader tube, pressure difference between A and B is found to be 310λN/m2. Here λ is an integer. Find λ (density = 103kg/m3, surface tension = 72×10−3N/m). (take g=9.8m/s2)
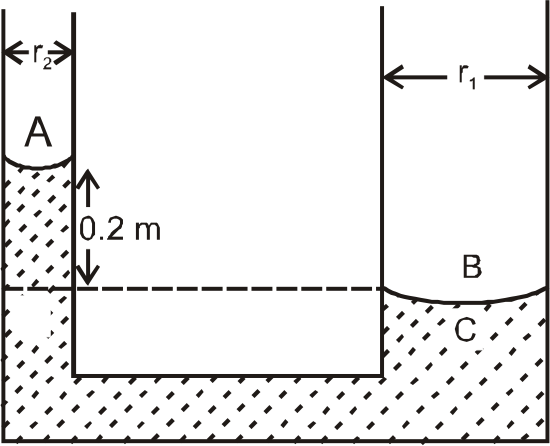 View Solution
View SolutionCalculate the height of liquid column required to balance the excess pressure inside a soap bubble of radius 3×10−3m .The density of liquid is 900kgm−3 and the surface tension of soap solution is 30×10−3Nm−1.
View SolutionTo what height does the liquid rise in a capillary tube of radus 0.25 mm, when dipped in a liquid of density 0.8×103kgm−3 and surface tension 0.05 N m−1? Given (cosθ=0.4)
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionFind the greatest length of steel wire that can hang vertically without breaking. Breaking stress of steel =8.0×108N/m2. Density of steel =8.0×103kg/m3. Take g=10m/s2.
View SolutionAt a depth of 500m in an ocean (a) what is the absolute pressure? (b) What is the gauge pressure? Density of sea water is 1.03×103kg/m3,g=10ms−2. Atmospheric pressure = 1.01×105Pa.
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View Solution

