In a large room , a person receives direct sound waves from a source 120m away . He also receives waves from the same source which reach him after being reflected from the 5m high ceiling at a point halfway between them . For which wavelengths will these two sound waves interfere constructively ?
10,10/2,10/3,10/4
20,20/3,20/5,20/7………
30,20,10,……..
10,10/3,10/5,10/7…….
The correct Answer is:A
To solve the problem, we need to determine the wavelengths for which the direct sound waves and the reflected sound waves interfere constructively.
1. Identify the Setup:
- The source of sound (S) is located 120 m away from the person (A).
- The sound waves also reach the person after reflecting off a ceiling that is 5 m high. The reflection occurs at a point halfway between the source and the person.
2. Calculate the Distance to the Reflection Point:
- The distance from the source (S) to the reflection point (O) is half of 120 m, which is 60 m.
- The height of the ceiling is 5 m.
3. Determine the Path of the Reflected Sound Wave:
- The path of the reflected sound wave is from the source (S) to the reflection point (O) and then to the person (A).
- The distance AO (from the reflection point to the person) is also 60 m.
4. Calculate the Total Distance for the Reflected Wave:
- The total distance for the reflected sound wave (S to O to A) can be calculated using the Pythagorean theorem:
Distance SO=√(602+52)=√3600+25=√3625≈60.41 m
- The total distance for the reflected wave is:
Total Distance=Distance SO+Distance OA=60.41 m+60 m=120.41 m
5. Calculate the Path Difference:
- The path difference (Δx) between the direct sound wave and the reflected sound wave is:
Δx=Total Distance (Reflected)−Direct Distance=120.41 m−120 m=0.41 m
6. Condition for Constructive Interference:
- For constructive interference, the path difference must be an integral multiple of the wavelength (λ):
Δx=nλwhere n is an integer
7. Calculate Wavelengths:
- Rearranging gives:
λ=Δxn=0.41n
- For different values of n (1, 2, 3, ...):
- For n=1: λ=0.41 m
- For n=2: λ=0.205 m
- For n=3: λ=0.1367 m
- And so on.
Final Answer:
The wavelengths for which the two sound waves will interfere constructively are given by:
λ=0.41n for n=1,2,3,…
- The source of sound (S) is located 120 m away from the person (A).
- The sound waves also reach the person after reflecting off a ceiling that is 5 m high. The reflection occurs at a point halfway between the source and the person.
- The distance from the source (S) to the reflection point (O) is half of 120 m, which is 60 m.
- The height of the ceiling is 5 m.
- The path of the reflected sound wave is from the source (S) to the reflection point (O) and then to the person (A).
- The distance AO (from the reflection point to the person) is also 60 m.
- The total distance for the reflected sound wave (S to O to A) can be calculated using the Pythagorean theorem:
Distance SO=√(602+52)=√3600+25=√3625≈60.41 m
- The total distance for the reflected wave is:
Total Distance=Distance SO+Distance OA=60.41 m+60 m=120.41 m
- The path difference (Δx) between the direct sound wave and the reflected sound wave is:
Δx=Total Distance (Reflected)−Direct Distance=120.41 m−120 m=0.41 m
- For constructive interference, the path difference must be an integral multiple of the wavelength (λ):
Δx=nλwhere n is an integer
- Rearranging gives:
λ=Δxn=0.41n
- For different values of n (1, 2, 3, ...):
- For n=1: λ=0.41 m
- For n=2: λ=0.205 m
- For n=3: λ=0.1367 m
- And so on.
The wavelengths for which the two sound waves will interfere constructively are given by:
λ=0.41n for n=1,2,3,…
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - II20videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - III19videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - II30videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise28videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
Similar Questions
In a hall, a person receives direct sound waves from a source 120m away. He also receives waves from the same source which reach him after being reflected from the 25m high ceiling at a point halfway between them. The two waves interfere constructively for wavelengths (in metres)
View SolutionIn a large room , a person receives direct sound waves from a source 120 metres away from him. He also receives waves from the same source which reach , being reflected from the 25m high ceiling at a point halfway between them . The two waves interfere constructively for a wavelength of
View SolutionA person standing at a distance of 6 m from a source of sound receives sound wave in two ways, one directly from the source and other after reflection from a rigid boundary as shown in the figure. The maximum wavelength for which, the person will receive maximum sound intensity, is
 View Solution
View SolutionA detector at x=0 receives waves from three sources each of amplitude A and frequencies f+2,f and f−2.
The time at which intensity is maximum, isView SolutionThe sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source ?
View SolutionTwo coherent sources A and B of radio waves are 5.00 m apart. Each source emits waves with wavelength 6.00m. Consider points along the line between the two sources. At what distances, if any, from A is the interference (a) constructive (b) destructive?
View SolutionA sound wave starting from source S, follows two paths AOBandACB to reach the detector D. If ABC is an equilateral traingle , of side l and there is silence at point D, the maximum wavelength (λ) of sound wave must be
 View Solution
View SolutionAn electromagnetic wave emitted by source travels 21 km to arrive at a receiver. The wave while travelling in another path is reflected from a surface at 19 km away and further travels 12 km to reach the same receiver. If destructive interference occurs at the receiving end, the mximum wavelength of the wave is
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
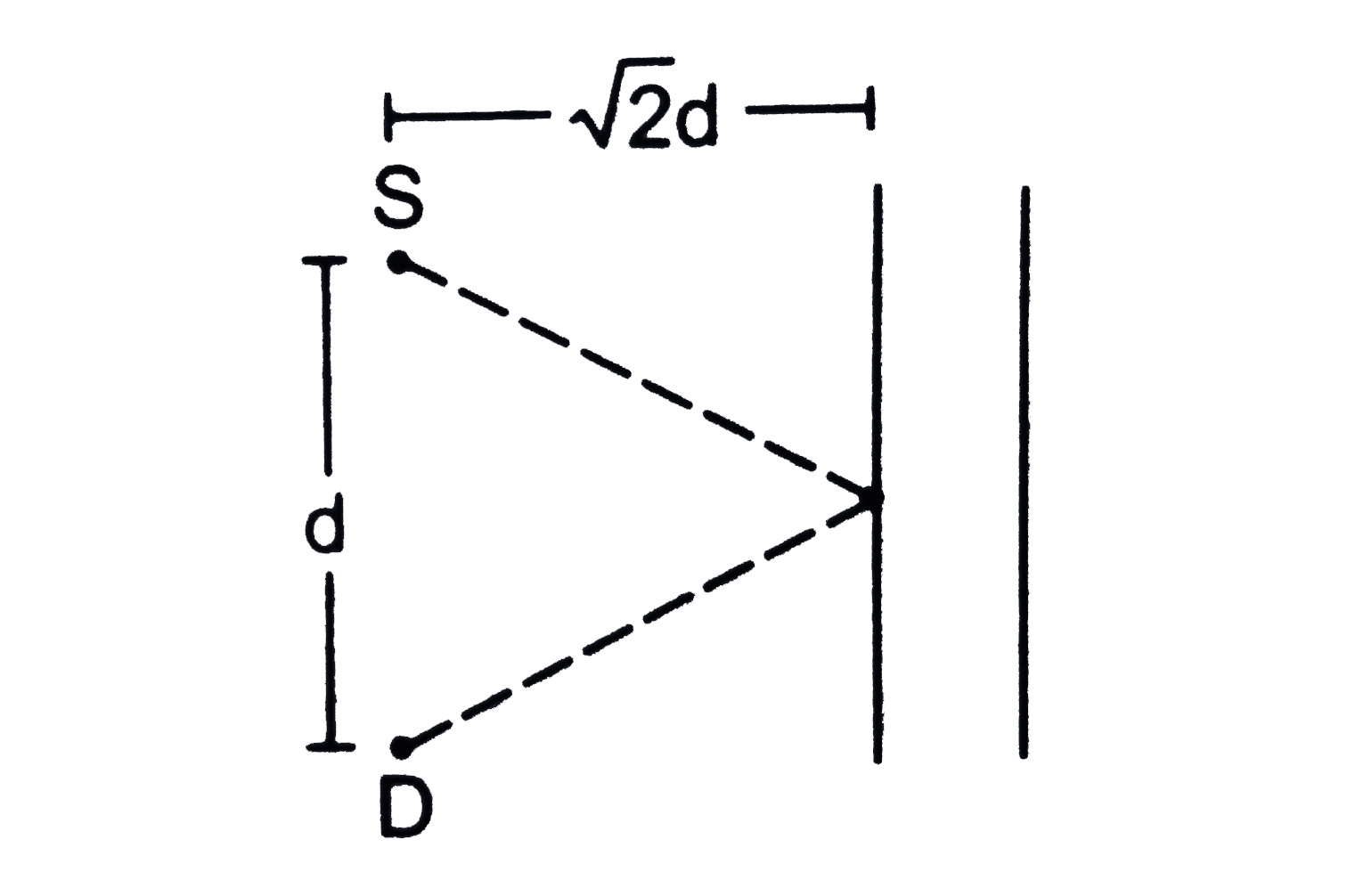 View Solution
View SolutionSound wave from a source A, follows two paths AOB and APQB in a tube as shown in figure. For silence at B, possible wavelength of sound will be
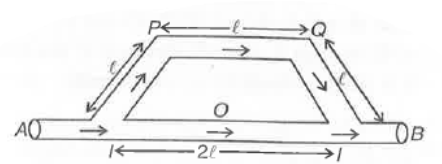 View Solution
View Solution

