A point sound is located in the perpendicular to the plane of a ring drawn through the centre O of the ring. The distance between the point O and the source is l=1.00m, the radius of the ring is R=0.50m. If the mean energy flow rate across the area encloseed by the ring is (in μW). Find x05. Given, at point O the energy intensity of sound is equal to I0=30μW/m2 and assuming the damping of the waves is negligible.
The correct Answer is:4
To solve the problem step by step, we will use the information given about the sound intensity and the geometry of the setup.
Step 1: Understand the Geometry
We have a point sound source located at a distance l=1.00m from the center O of a ring with radius R=0.50m. The sound waves emitted from the source will spread out in a spherical manner.
Step 2: Calculate the Area of the Ring
The area A of the ring can be approximated as the area of a circle with radius R:
A=πR2=π(0.50)2=π4m2
Step 3: Understand the Intensity
The intensity of sound at point O is given as I0=30μW/m2. Intensity is defined as power per unit area.
Step 4: Calculate the Total Power at Point O
The total power P radiated by the source can be calculated using the intensity at point O:
P=I0×A=30μW/m2×π4m2
Calculating this gives:
P=30×π4μW≈23.56μW
Step 5: Calculate the Energy Flow Rate Across the Area Enclosed by the Ring
The mean energy flow rate across the area enclosed by the ring can be computed using the total power and the area:
Energy Flow Rate=PA=30μWπ/4=120μWπ≈38.2μW
Step 6: Find x05
Since the problem asks for x05 and we have found the energy flow rate to be approximately 38.2μW, we can denote this value as x0:
x0=38.2μW
Thus,
x05=38.25≈7.64μW
Final Answer
x05≈7.64μW
---
We have a point sound source located at a distance l=1.00m from the center O of a ring with radius R=0.50m. The sound waves emitted from the source will spread out in a spherical manner.
The area A of the ring can be approximated as the area of a circle with radius R:
A=πR2=π(0.50)2=π4m2
The intensity of sound at point O is given as I0=30μW/m2. Intensity is defined as power per unit area.
The total power P radiated by the source can be calculated using the intensity at point O:
P=I0×A=30μW/m2×π4m2
Calculating this gives:
P=30×π4μW≈23.56μW
The mean energy flow rate across the area enclosed by the ring can be computed using the total power and the area:
Energy Flow Rate=PA=30μWπ/4=120μWπ≈38.2μW
Since the problem asks for x05 and we have found the energy flow rate to be approximately 38.2μW, we can denote this value as x0:
x0=38.2μW
Thus,
x05=38.25≈7.64μW
x05≈7.64μW
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - III19videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - IV8videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I24videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise28videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
Similar Questions
What is the distance of centre of mass of a half fring from centre if the ring has radius =0.5 m [XI]
View SolutionFind the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of this particles.
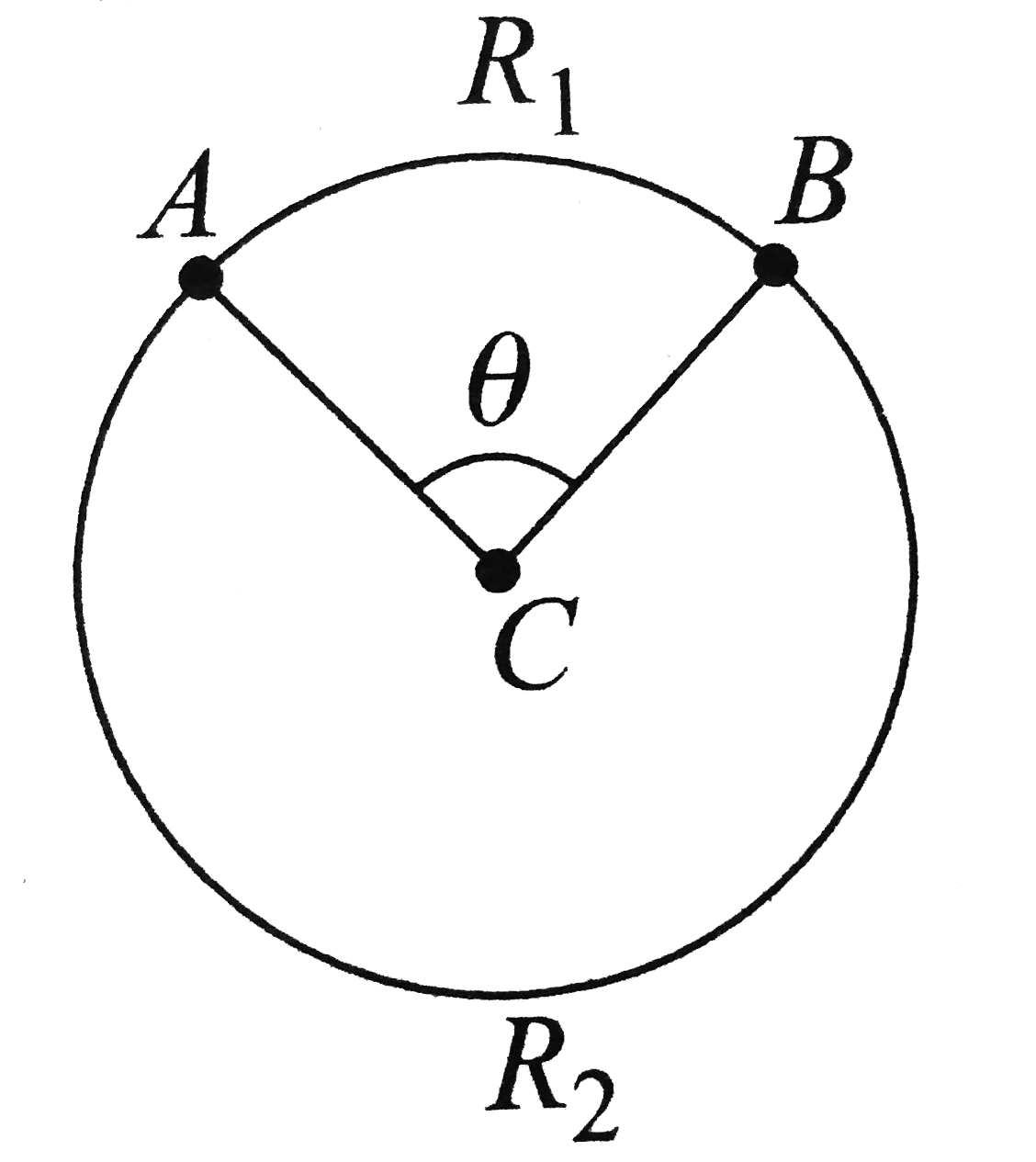
View SolutionIn a uniform ring of resistance R there are two points A and B such that ∠ACB=θ, where C is the centre of the ring. The equivalent resistance between A and B is
 View Solution
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
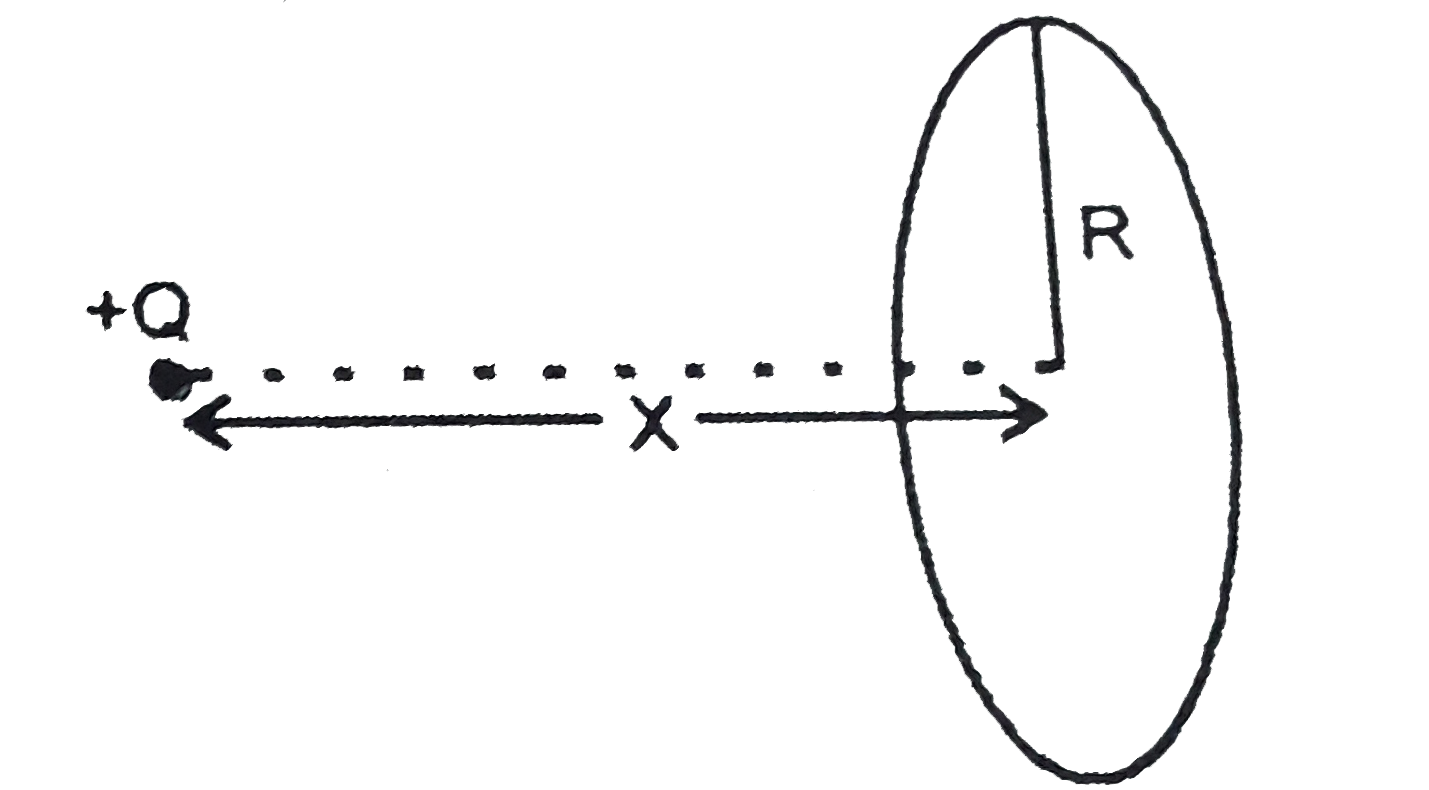
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
 View Solution
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
 View Solution
View Solution

