
In the adjacent figure ABC is a uniform isosceles triangular lamina of mass m and AB=AC=l the lamina is free to rotate about a fixed horizontal axis OAO′ which is in the plane of the lamina. Initially the lamina is in static equilibrium with maximum gravitational potential energy. due to slight disturbance, lamina starts rotating. Now choose the correct option(s)
The maximum angular speed acquired by lamina is 4√√2g3l
The maximum vertical force on the axis by the lamina is 419mg
Angular momentum of the lamina about OAO' is conserve
When the lamina acquire maximum angular speed acceleration of centre of mass is zero
The correct Answer is:A, B, C, D
∵−ΔU=ΔK
2√2mgl3=12.ml2ω24
(moment of inertia aboutOAO'=ml24)
⇒ω=√16√23.gl=4√√2g3l
F−mg=mω2R=m×16√2g3l.√2l3
⇒F+mg+32mg9−41mg9
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
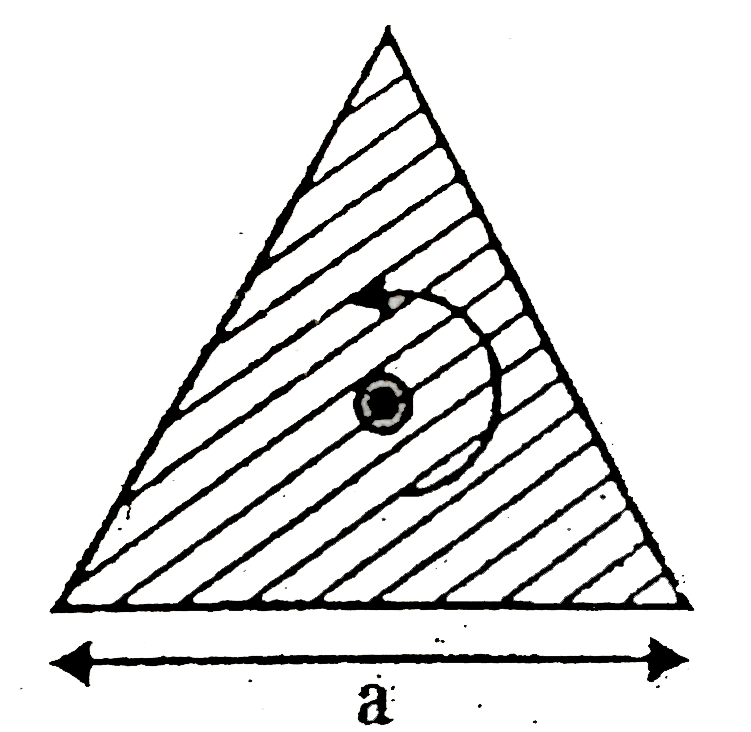
A uniform equilateral triangular lamina of side a has mass m. Its moment of inertia about the axis passing through the centroid and prependicular to the plane of the lamina is :-
View SolutionFind MI of a triangular lamina of mass M about the axis of rotation AB shown in Fig.

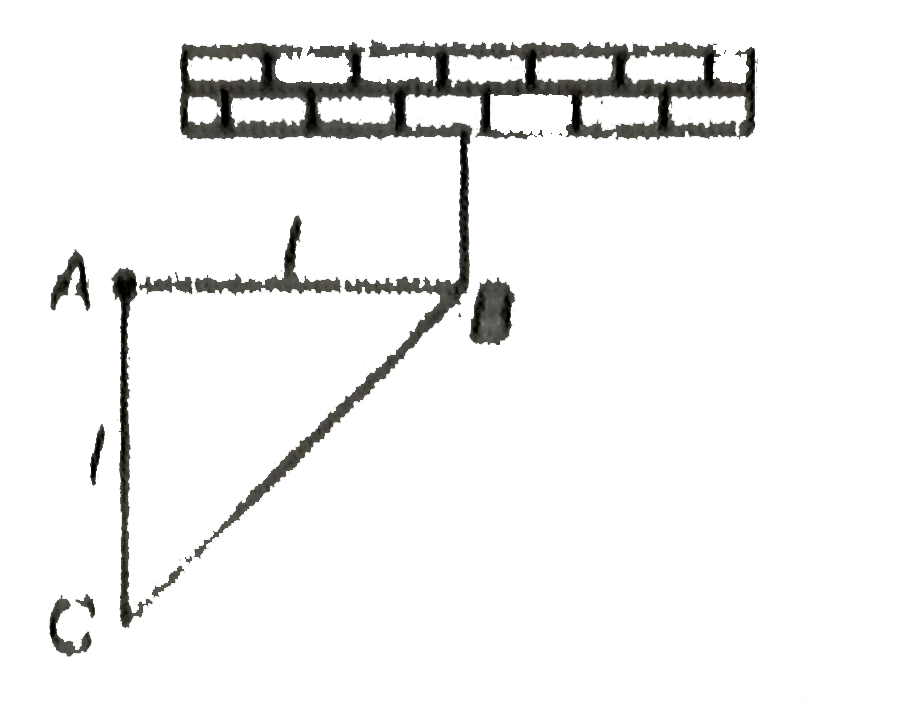
View SolutionA right triangular plate ABC of mass m is free to rotate in the verticle plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionABC is a triangular framwork of three uniform rods each of mass m and length 2l. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
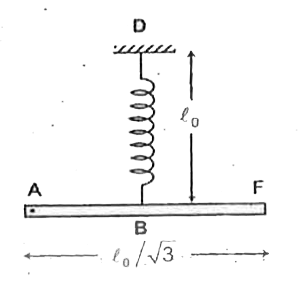
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA uniform rod of mass M and length L, which is free to rotate about a fixed vertical axis through O, is lying on a frictionless horizontal table. A particle of equal mass strikes the rod with a velocity V0 and sticks to it. The angular velocity of the combination immediately after the collision is:
View SolutionA thin rod of mass m and length l is free to rotate on a smooth horizontal plane about its one fixed end. When it is at rest, it receives a horizontal impulse J at its other end, at angle of 37∘ with the length. Choose incorrect option immediately after impact:
View SolutionFigure shows a solid uniform cylinder of radius R and mass M, which is free to rotate about a fixed horizontal axis O and passes through centre of the cylinder. One end of an ideal spring of force constant k is fixed and the other end is higed to the cylinder at A. Distance OA is equal to R2. An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass M and having cross sectional area A is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density ρ.
If in equilibrium, spring is horizontal and line OA is vertical, calculate frequency of small oscillations of the system.

View SolutionA uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
View Solution
