A soap bubble (surface tension=T) is charged to maximum surface density of charge=σ. When it is just going to burst. Its radius R is given by:
R=σ28ε0T
R=8ε0Tσ2
R=σ√8(ε0T)
R=√8ε0Tσ
The correct Answer is:B
To find the radius R of a soap bubble that is just about to burst when it is charged to a maximum surface charge density σ, we can follow these steps:
Step 1: Understand the pressures involved
When a soap bubble is charged, two types of pressures act on it:
1. Pressure due to surface tension Ps
2. Pressure due to electric charge Pe
Step 2: Write the expression for pressure due to surface tension
The pressure inside the soap bubble due to surface tension is given by the formula:
Ps=4TR
where T is the surface tension and R is the radius of the bubble.
Step 3: Write the expression for pressure due to electric charge
The pressure inside the soap bubble due to the electric charge is given by:
Pe=σ22ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
Step 4: Set the pressures equal to each other
When the soap bubble is just about to burst, the pressure due to surface tension equals the pressure due to the electric charge:
Pe=Ps
Substituting the expressions from Steps 2 and 3, we get:
σ22ϵ0=4TR
Step 5: Solve for the radius R
Rearranging the equation to solve for R:
R=4T⋅2ϵ0σ2
This simplifies to:
R=8Tσ2
Conclusion
Thus, the radius R of the soap bubble when it is just going to burst is given by:
R=8Tσ2
When a soap bubble is charged, two types of pressures act on it:
1. Pressure due to surface tension Ps
2. Pressure due to electric charge Pe
The pressure inside the soap bubble due to surface tension is given by the formula:
Ps=4TR
where T is the surface tension and R is the radius of the bubble.
The pressure inside the soap bubble due to the electric charge is given by:
Pe=σ22ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
When the soap bubble is just about to burst, the pressure due to surface tension equals the pressure due to the electric charge:
Pe=Ps
Substituting the expressions from Steps 2 and 3, we get:
σ22ϵ0=4TR
Rearranging the equation to solve for R:
R=4T⋅2ϵ0σ2
This simplifies to:
R=8Tσ2
Thus, the radius R of the soap bubble when it is just going to burst is given by:
R=8Tσ2
Topper's Solved these Questions
Similar Questions
A spherical charged conductor has surface density of charge as σ. The electric field intensity on its surface is E. If the radius of the surface is doubled, keeping σ uncharged, what will be the electric field intensity on the new sphere ?
View SolutionFor gaseous reactions, if ΔH is the change in enthalpy and ΔU that in internal energy, then
View Solution
Knowledge Check
- Question 1 - Select One
The work done to blow a scap bubble of radius. R (surface tension T)
A4πr2TBπr2TC2πr2TD8πr2T
What is the surface energy of a soap bubble of radus r and surface tension T?
View SolutionWhen a soap bubble is charged :-
View SolutionA soap bubble of radius 'r' and surface tension 'T' is given a potential of 'V' volt. If the new radiys 'R' of the bubble is related to its initial radius by equation.
P0[R3−r3]+[λT[R2−r2]−ε0V2R/2=0, where P0 is the atmospheric pressure. Then find λView SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionShow in the figure are two point charge + Q and - Q inside the cavity of the Spherical .shell the changes are kept near the surface of the cavity on opposite sides of the centre of the shell if σ1 is the surface charge on the inner surface and Q1 net charge on it and σ2 the surface charge on the outer surface and Q2 net charge on it then :
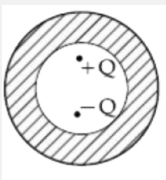 View Solution
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View Solution

