Suppose the earth suddenly shrinks in size, still remaining spherical and mass unchanged (All gravitational forces pass through the centre of the earth).
The days will become shorter.
The kinetic energy of rotation about its own axis will decrease
The duration of the year will increase
The magnitude of angular momentum about its axis will increase.
The correct Answer is:A
To solve the problem of what happens when the Earth suddenly shrinks in size while keeping its mass unchanged, we can analyze the situation using the principles of angular momentum, moment of inertia, and rotational motion.
1. Understanding Angular Momentum Conservation:
- Angular momentum (L) is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
- Since the mass of the Earth remains unchanged and it is shrinking, the angular momentum will be conserved.
2. Moment of Inertia:
- The moment of inertia I for a solid sphere is given by:
I=25mr2
where m is the mass and r is the radius.
- As the Earth shrinks, the radius r decreases, leading to a decrease in the moment of inertia I.
3. Effect on Angular Velocity:
- Since angular momentum is conserved:
I1⋅ω1=I2⋅ω2
where I1 and ω1 are the initial moment of inertia and angular velocity, and I2 and ω2 are the new moment of inertia and angular velocity after shrinking.
- If I2<I1 (moment of inertia decreases), then ω2 must increase to keep the product I⋅ω constant.
4. Time Period of Rotation:
- The time period T of rotation is given by:
T=2πω
- Since ω increases, T must decrease. This means that the Earth will complete its rotation in a shorter period of time.
5. Kinetic Energy of Rotation:
- The rotational kinetic energy K is given by:
K=12Iω2
- As ω increases and I decreases, the overall kinetic energy will increase because the increase in ω2 will dominate.
6. Conclusion:
- The days on Earth will become shorter due to the increase in angular velocity.
- The kinetic energy of the Earth's rotation will increase.
- The duration of the year (time taken to orbit the sun) is not directly affected by the change in size but is related to the orbital mechanics, which remains unchanged in this scenario.
Final Statements:
- Correct Statement: The days will become shorter.
- Incorrect Statements: Kinetic energy of rotation decreases, duration of the year increases, and the magnitude of angular momentum decreases.
- Angular momentum (L) is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
- Since the mass of the Earth remains unchanged and it is shrinking, the angular momentum will be conserved.
- The moment of inertia I for a solid sphere is given by:
I=25mr2
where m is the mass and r is the radius.
- As the Earth shrinks, the radius r decreases, leading to a decrease in the moment of inertia I.
- Since angular momentum is conserved:
I1⋅ω1=I2⋅ω2
where I1 and ω1 are the initial moment of inertia and angular velocity, and I2 and ω2 are the new moment of inertia and angular velocity after shrinking.
- If I2<I1 (moment of inertia decreases), then ω2 must increase to keep the product I⋅ω constant.
- The time period T of rotation is given by:
T=2πω
- Since ω increases, T must decrease. This means that the Earth will complete its rotation in a shorter period of time.
- The rotational kinetic energy K is given by:
K=12Iω2
- As ω increases and I decreases, the overall kinetic energy will increase because the increase in ω2 will dominate.
- The days on Earth will become shorter due to the increase in angular velocity.
- The kinetic energy of the Earth's rotation will increase.
- The duration of the year (time taken to orbit the sun) is not directly affected by the change in size but is related to the orbital mechanics, which remains unchanged in this scenario.
- Correct Statement: The days will become shorter.
- Incorrect Statements: Kinetic energy of rotation decreases, duration of the year increases, and the magnitude of angular momentum decreases.
Topper's Solved these Questions
Similar Questions
Is it necessary for the plane of the orbit of a satellite to pass through the Centre of the earth?
View SolutionThe free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is a. at te equaltor b. at a pole c. somewhere else.
View SolutionStatement I: In free space a uniform spherical planet of mass M has a smooth narrow tunnel along its diameter. This planet and another superdense small particle of mass M start approaching towards each other from rest under action of their gravitational forces. When the particle passes through the centre of the planet, sum of kinetic energies of both the bodies is maximum.
Statement II: When the resultant of all forces acting on a particle or a particle like object (initially at rest) is constant in direction, the kinetic energy of the particle keeps on increasing.View SolutionInside a fixed sphere of radius R and uniform density ρ, there is spherical cavity of radius R2 such that surface of the cavity passes through the centre of the sphere as shows in figure. A particle of mass m0 is released from rest at centre B of the cavity. Caculate velocity with which particle strikes the centre A of the sphere. Neglect earth's gravity. Initially sphere and particle are at rest.
 View Solution
View SolutionIf the earth suddenly shrinks (without changing mass) to half of its present radius, then acceleration due to gravity will be
View SolutionThe value of g at a particular point is 10ms−2. Suppose the earth shrinks uniformly to half of its present size without losing any mass. The value of g at the same point (assuming that the distance of the point from the centre of the earth does not change) will now be
View SolutionCalculate the gravitational potential energy of a body of mass 100 kg at a distance of 6 km from the centre of the earth.
View SolutionUsing the formula for the moment of inertia of a uniform sphere, find the moment of inertia of a thin spherical layer of mass m and radius R relative to the axis passing through its centre.
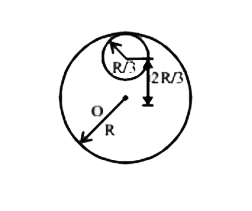
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
 View Solution
View SolutionIf the diameter of the earth becomes two times its present value and its mass remains unchanged then how would the weight of an object on the surface of the earth be affected ?
View Solution

