The focal length of a convex mirror is obtained by using a convex lens The following observations are recorded during theexperiment .
objectopsition=5cmlens=35.4cmImage=93.8cmMirror=63.3cmBencherror=−0.1cm
then the focal length of mirror will be .
7.5
8.4cm
15.3cm
None of these
The correct Answer is:C
To find the focal length of a convex mirror using the provided observations, we can follow these steps:
Step 1: Understand the Given Data
We have the following observations:
- Object position (u) = -5 cm (the object distance is taken as negative in lens/mirror formula)
- Lens position (v_lens) = 35.4 cm
- Image position (v_image) = 93.8 cm
- Mirror position (v_mirror) = 63.3 cm
- Bench error = -0.1 cm
Step 2: Calculate the Distance from the Image to the Mirror
To find the distance from the image to the mirror, we need to calculate:
R=vimage−vmirror
Substituting the values:
R=93.8cm−63.3cm=30.5cm
Step 3: Account for the Bench Error
Since there is a bench error of -0.1 cm, we need to adjust the calculated radius of curvature:
Rtrue=R+bench error
Rtrue=30.5cm−0.1cm=30.4cm
Step 4: Calculate the Focal Length
The focal length (f) of a convex mirror is related to the radius of curvature (R) by the formula:
f=R2
Substituting the true radius of curvature:
f=30.4cm2=15.2cm
Final Answer
Thus, the focal length of the convex mirror is:
f=15.2cm
---
We have the following observations:
- Object position (u) = -5 cm (the object distance is taken as negative in lens/mirror formula)
- Lens position (v_lens) = 35.4 cm
- Image position (v_image) = 93.8 cm
- Mirror position (v_mirror) = 63.3 cm
- Bench error = -0.1 cm
To find the distance from the image to the mirror, we need to calculate:
R=vimage−vmirror
Substituting the values:
R=93.8cm−63.3cm=30.5cm
Since there is a bench error of -0.1 cm, we need to adjust the calculated radius of curvature:
Rtrue=R+bench error
Rtrue=30.5cm−0.1cm=30.4cm
The focal length (f) of a convex mirror is related to the radius of curvature (R) by the formula:
f=R2
Substituting the true radius of curvature:
f=30.4cm2=15.2cm
Thus, the focal length of the convex mirror is:
f=15.2cm
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise -1 PART
1 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART II
13 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
Similar Questions
Focal length of a convex mirror is 10 cm
View SolutionThe focal length of a convex mirror is 20 cm its radius of curvature will be
View SolutionThe radius of curvature of a convex mirror is 40 cm. Find its focal length.
View SolutionFocal length of a convex lense in air is 20cm. and of concave lens 40cm. Find the position of final image.
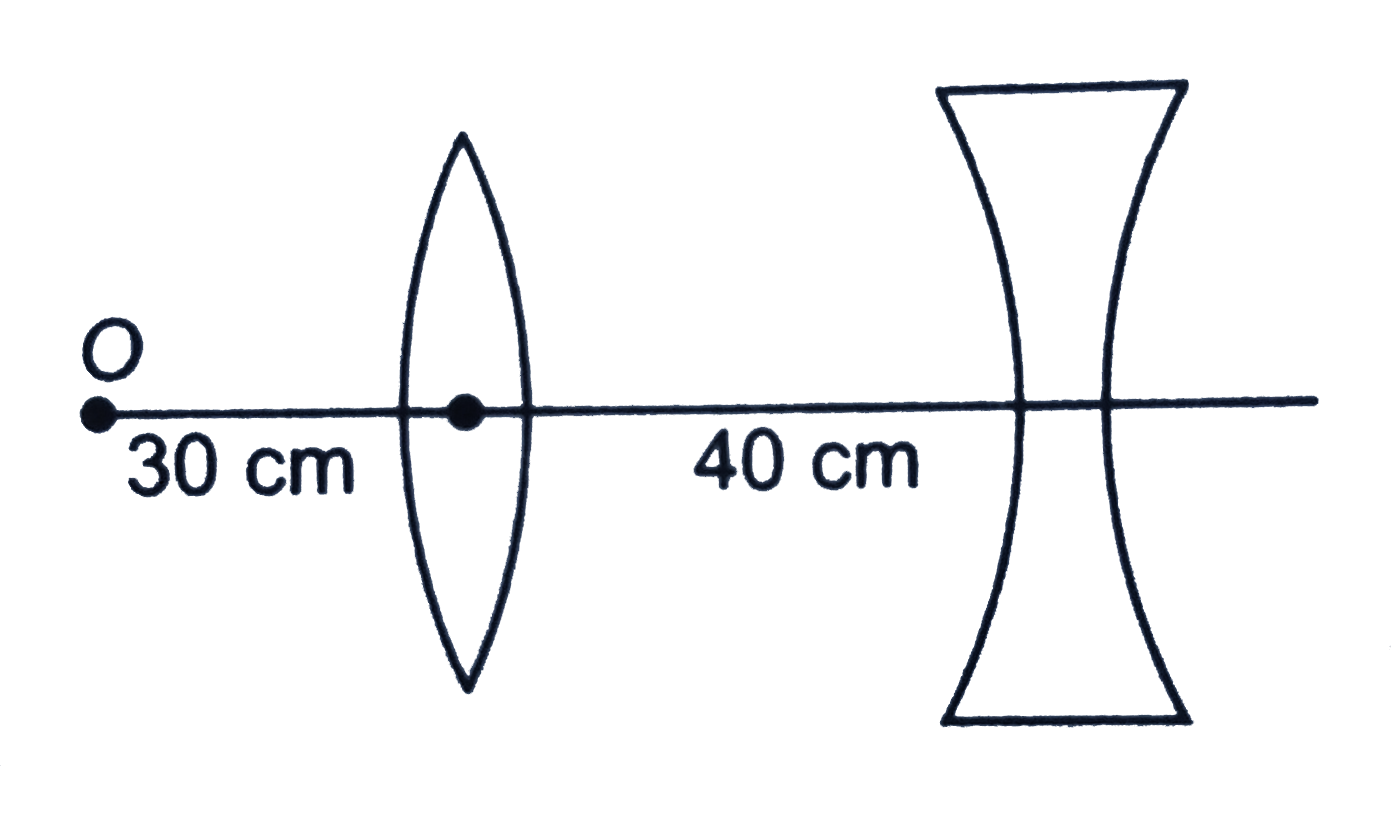
View SolutionThe focal length of a convex mirror is 40 cm. A point source of light is kept at distance 40 cm from the mirror. Find the distance of image from the mirror.
View SolutionTo find the focal length of a convex mirror , a student records the following data:
Object PinConvex LensConvex mirrorImage Pin22.2cm32.2cm45.8cm71.2cm
The focal length of the convex lens is f1 and that of mirror is f2 . Then taking index correction to be negligibly small , f1 and f2 are close to :
View Solution(a) What is focal length of a convex mirror of radius of curvature 20cm?
(b) What is radius of curvature of a mirror of focal length −50cm ?
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionA convex lens of focal length 80 cm and a concave lens of focal length 50 cm are combined toghether. What will be their resulting power ?
View Solution
