To find the focal length of a convex mirror , a student records the following data:
Object PinConvex LensConvex mirrorImage Pin22.2cm32.2cm45.8cm71.2cm
The focal length of the convex lens is f1 and that of mirror is f2 . Then taking index correction to be negligibly small , f1 and f2 are close to :
f1=7.8cm f2=12.7cm
f1=15.6cm f2=25.6cm
f1=12.7cm f2=7.8cm
f1=7.8cm f2=25.4cm
The correct Answer is:A
To find the focal lengths of the convex lens and the convex mirror based on the given data, we can follow these steps:
Step 1: Identify the given data
- Object distance for the convex lens (u) = 32.2 cm - 22.2 cm = 10 cm (but it will be negative)
- Image distance for the convex lens (v) = 71.2 cm - 32.2 cm = 39 cm
- Object distance for the convex mirror (u') = 22.2 cm - 45.8 cm = -23.6 cm (since it's virtual)
- Image distance for the convex mirror (v') = 71.2 cm - 45.8 cm = 25.4 cm
Step 2: Calculate the focal length of the convex lens (f1)
Using the lens formula:
1f=1v−1u
Substituting the values:
1f1=139−1−10
Calculating:
1f1=139+110
Finding a common denominator (390):
1f1=10390+39390=49390
Thus,
f1=39049≈7.8 cm
Step 3: Calculate the focal length of the convex mirror (f2)
The radius of curvature (R) is given by:
R=25.4 cm
The focal length of a convex mirror is given by:
f2=R2=25.42=12.7 cm
Step 4: Final results
Thus, the focal lengths are:
- Focal length of convex lens (f1) = 7.8 cm
- Focal length of convex mirror (f2) = 12.7 cm
Conclusion
The values of f1 and f2 are approximately 7.8 cm and 12.7 cm, respectively.
---
- Object distance for the convex lens (u) = 32.2 cm - 22.2 cm = 10 cm (but it will be negative)
- Image distance for the convex lens (v) = 71.2 cm - 32.2 cm = 39 cm
- Object distance for the convex mirror (u') = 22.2 cm - 45.8 cm = -23.6 cm (since it's virtual)
- Image distance for the convex mirror (v') = 71.2 cm - 45.8 cm = 25.4 cm
Using the lens formula:
1f=1v−1u
Substituting the values:
1f1=139−1−10
Calculating:
1f1=139+110
Finding a common denominator (390):
1f1=10390+39390=49390
Thus,
f1=39049≈7.8 cm
The radius of curvature (R) is given by:
R=25.4 cm
The focal length of a convex mirror is given by:
f2=R2=25.42=12.7 cm
Thus, the focal lengths are:
- Focal length of convex lens (f1) = 7.8 cm
- Focal length of convex mirror (f2) = 12.7 cm
The values of f1 and f2 are approximately 7.8 cm and 12.7 cm, respectively.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (B)
35 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - MCQ
5 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[B]
18 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Focal length of a convex mirror is 10 cm
View SolutionThe focal length of a convex mirror is 20 cm its radius of curvature will be
View SolutionThe radius of curvature of a convex mirror is 40 cm. Find its focal length.
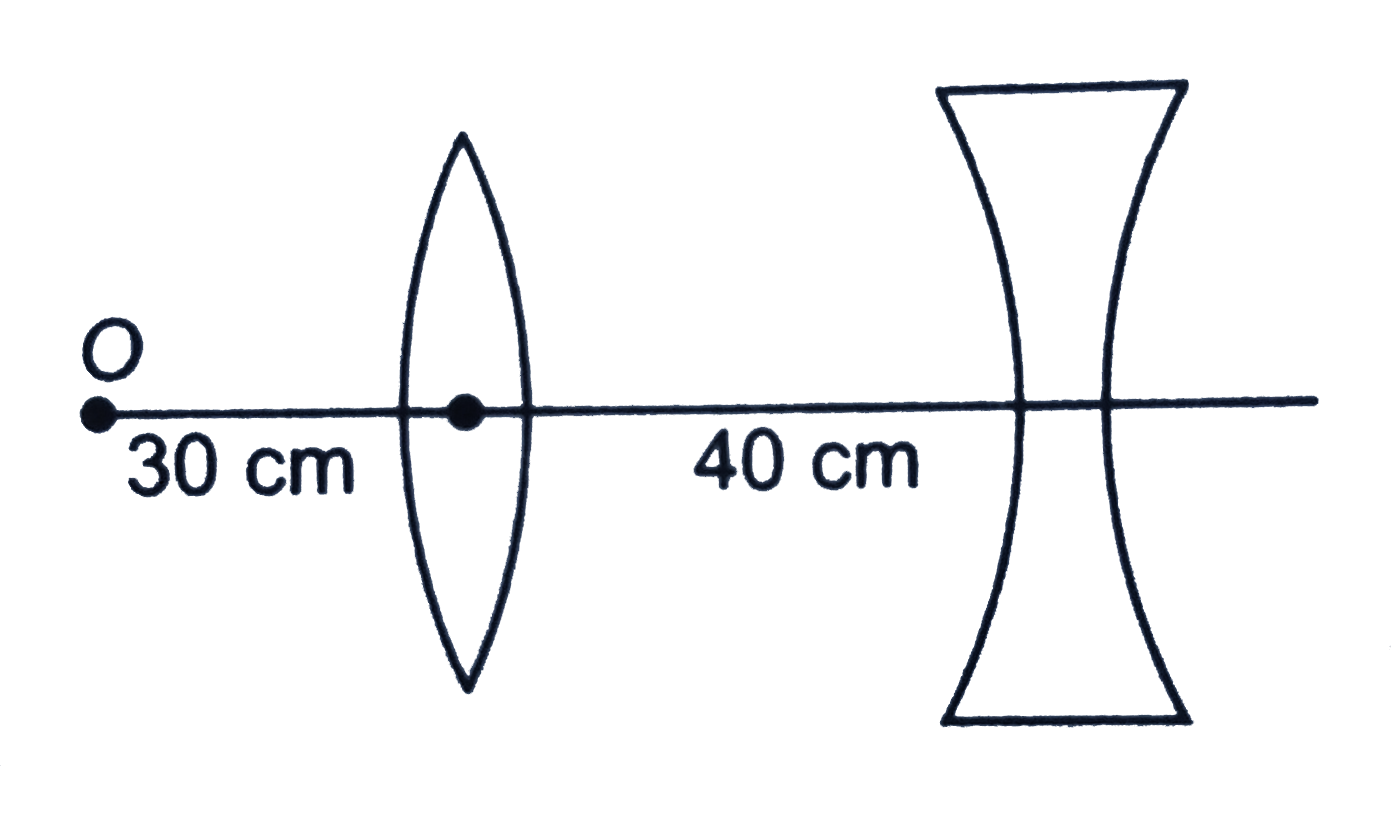
View SolutionFocal length of a convex lense in air is 20cm. and of concave lens 40cm. Find the position of final image.
View SolutionFocal length of convex mirror M1 is 20 cm and that of concave mirror M2 is 30 cm .Find position of second image I2.Take first reflection from M1.

View SolutionThe focal length of a convex mirror is obtained by using a convex lens The following observations are recorded during theexperiment .
objectopsition=5cmlens=35.4cmImage=93.8cmMirror=63.3cmBencherror=−0.1cm
then the focal length of mirror will be .
View SolutionA convex mirror of focal length f produced an image (1/n)th of the size of the object. The distance of the object from the mirror is
View SolutionThe focal length of a convex mirror is 40 cm. A point source of light is kept at distance 40 cm from the mirror. Find the distance of image from the mirror.
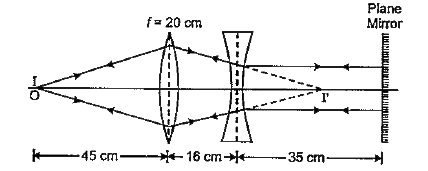
View SolutionThe figure below shows the positions of a point object 0, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
View SolutionA point light source is kept in front of a convex mirror at a distance of 40 cm. The focal length of the mirror is 40 cm. Find the position of image.
View Solution
