In the decomposition of H2O2 at 300 K, the energy of activation was found to be 18kcal/mol white it decreases to 6kcal/mol when the decomposition was carried out in the presence of a catalyst at 300 K. The number of times the catalysed reaction faster than uncatalysed one is (Give you answer by multiplying 107)
The correct Answer is:48 times
To solve the problem, we will use the Arrhenius equation, which relates the rate constant (k) of a reaction to its activation energy (E_a) and temperature (T).
1. Identify the Activation Energies:
- For the uncatalyzed reaction, the activation energy Eu=18kcal/mol=18000cal/mol.
- For the catalyzed reaction, the activation energy Ec=6kcal/mol=6000cal/mol.
2. Write the Arrhenius Equation:
The Arrhenius equation is given by:
k=A⋅e−EaRT
where:
- k = rate constant
- A = pre-exponential factor (constant)
- Ea = activation energy
- R = gas constant (2 cal/(mol·K))
- T = temperature in Kelvin (300 K)
3. Calculate the Rate Constants:
- For the uncatalyzed reaction:
ku=A⋅e−EuRT=A⋅e−180002⋅300
- For the catalyzed reaction:
kc=A⋅e−EcRT=A⋅e−60002⋅300
4. Take the Ratio of Rate Constants:
The ratio of the rate constants for the catalyzed and uncatalyzed reactions is:
kcku=A⋅e−6000600A⋅e−18000600=e−6000600+18000600=e12000600=e20
5. Calculate e20:
Using a calculator or approximation:
e20≈4.85×108
6. Multiply by 107:
The problem asks for the number of times the catalyzed reaction is faster than the uncatalyzed reaction, multiplied by 107:
4.85×108×107=4.85×1015
Final Answer:
The number of times the catalyzed reaction is faster than the uncatalyzed reaction, after multiplying by 107, is:
4.85×1015
- For the uncatalyzed reaction, the activation energy Eu=18kcal/mol=18000cal/mol.
- For the catalyzed reaction, the activation energy Ec=6kcal/mol=6000cal/mol.
The Arrhenius equation is given by:
k=A⋅e−EaRT
where:
- k = rate constant
- A = pre-exponential factor (constant)
- Ea = activation energy
- R = gas constant (2 cal/(mol·K))
- T = temperature in Kelvin (300 K)
- For the uncatalyzed reaction:
ku=A⋅e−EuRT=A⋅e−180002⋅300
- For the catalyzed reaction:
kc=A⋅e−EcRT=A⋅e−60002⋅300
The ratio of the rate constants for the catalyzed and uncatalyzed reactions is:
kcku=A⋅e−6000600A⋅e−18000600=e−6000600+18000600=e12000600=e20
Using a calculator or approximation:
e20≈4.85×108
The problem asks for the number of times the catalyzed reaction is faster than the uncatalyzed reaction, multiplied by 107:
4.85×108×107=4.85×1015
The number of times the catalyzed reaction is faster than the uncatalyzed reaction, after multiplying by 107, is:
4.85×1015
Topper's Solved these Questions
Similar Questions
Given : A⇔B+C,ΔH=−10 kcals, the energy of activation of backward reaction is 15 kcal mol−1. If the energy of activation of forward reaction in the presence of a catalyst is 3 kcal mol−1 the catalyst will increase the rate of reaction at 300 K by the number of times equal to
View SolutionThe activation energy of a first order reaction at 300K is 60 kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
View SolutionAt 400K , the energy of activation of a reaction is decreased by 0.8Kcal in the presence of catalyst. Hence, the rate will be
a. Increased by 2.73 times
b. Increased by 1.18 times
c. Decreased by 2.72 times
d. Increased by 6.26 timesView SolutionThe major product of the following reaction is:
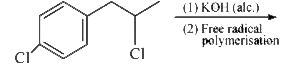 View Solution
View SolutionThe rate constant for the decomposition of hydrocarbons is 2.418×10–5s–1 at 546 K. If the energy of activation is 179.9kJ/mol, what will be the value of pre-exponential factor.
View SolutionThe rate constant for the decomposition of hydrocarbons is 2.418×10–5s–1 at 546 K. If the energy of activation is 179.9kJ/mol, what will be the value of pre-exponential factor.
View SolutionThe rate constant for the decomposition of hydrocarbons is 2.418×10–5s–1 at 546 K. If the energy of activation is 179.9kJ/mol, what will be the value of pre-exponential factor.
View SolutionThe activation energy of a reaction is 50 kJ mol-1 and the value of rate constant at 300 K is 2.5×10−5sec−1. What is the value of the frequency factor, A?
View SolutionThe activation energy for a reaction is 9 kcal/mol. The increase in late (XI 'slant when its temperature is increased from 298K to 308 K is (R=2calK−1mot−1,100.213=1.63)
View SolutionFor a reaction the activation energy Ea=0 and the rate constant=3.2×106sec−1 at 300K. What is the value of rate constant at 310K?
View Solution

