Compound pendulum are made of A rod of length l suspended through a point located at distance l/4 from centre of rod. Find the time period in each case.
The correct Answer is:(a) T=2π√7l12g , (b) 2π√2rg
(c) 2π√√8a3g,2π√3r2g
To find the time period of a compound pendulum made of a rod of length l suspended through a point located at a distance l4 from the center of the rod, we can follow these steps:
1. Understanding the Formula for Time Period:
The time period T of a compound pendulum is given by the formula:
T=2π√Icm+m⋅d2m⋅g⋅d
where:
- Icm is the moment of inertia about the center of mass,
- m is the mass of the pendulum,
- g is the acceleration due to gravity,
- d is the distance from the center of mass to the point of suspension.
2. Calculating Moment of Inertia for the Rod:
The moment of inertia Icm of a uniform rod about its center is given by:
Icm=112ml2
3. Finding the Distance d:
The distance d from the center of mass to the point of suspension is given as l4.
4. Substituting Values into the Formula:
Now substituting Icm and d into the time period formula:
T=2π
⎷112ml2+m(l4)2mg⋅l4
5. Simplifying the Expression:
Calculate m(l4)2:
m(l4)2=m⋅l216
Therefore:
T=2π
⎷112ml2+116ml2mg⋅l4
6. Finding a Common Denominator:
The common denominator for 112 and 116 is 48:
112=448,116=348
Thus:
112ml2+116ml2=4ml2+3ml248=7ml248
7. Substituting Back into the Time Period Formula:
Now substituting back:
T=2π
⎷7ml248mg⋅l4
8. Simplifying Further:
The m cancels out:
T=2π
⎷7l248⋅g⋅l4
Simplifying the denominator:
g⋅l4=gl4
So:
T=2π
⎷7l248⋅gl4=2π√7⋅4l48g=2π√28l48g=2π√7l12g
9. Final Result:
Thus, the time period T of the compound pendulum is:
T=2π√7l12g
The time period T of a compound pendulum is given by the formula:
T=2π√Icm+m⋅d2m⋅g⋅d
where:
- Icm is the moment of inertia about the center of mass,
- m is the mass of the pendulum,
- g is the acceleration due to gravity,
- d is the distance from the center of mass to the point of suspension.
The moment of inertia Icm of a uniform rod about its center is given by:
Icm=112ml2
The distance d from the center of mass to the point of suspension is given as l4.
Now substituting Icm and d into the time period formula:
T=2π
⎷112ml2+m(l4)2mg⋅l4
Calculate m(l4)2:
m(l4)2=m⋅l216
Therefore:
T=2π
⎷112ml2+116ml2mg⋅l4
The common denominator for 112 and 116 is 48:
112=448,116=348
Thus:
112ml2+116ml2=4ml2+3ml248=7ml248
Now substituting back:
T=2π
⎷7ml248mg⋅l4
The m cancels out:
T=2π
⎷7l248⋅g⋅l4
Simplifying the denominator:
g⋅l4=gl4
So:
T=2π
⎷7l248⋅gl4=2π√7⋅4l48g=2π√28l48g=2π√7l12g
Thus, the time period T of the compound pendulum is:
T=2π√7l12g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II
36 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I
26 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
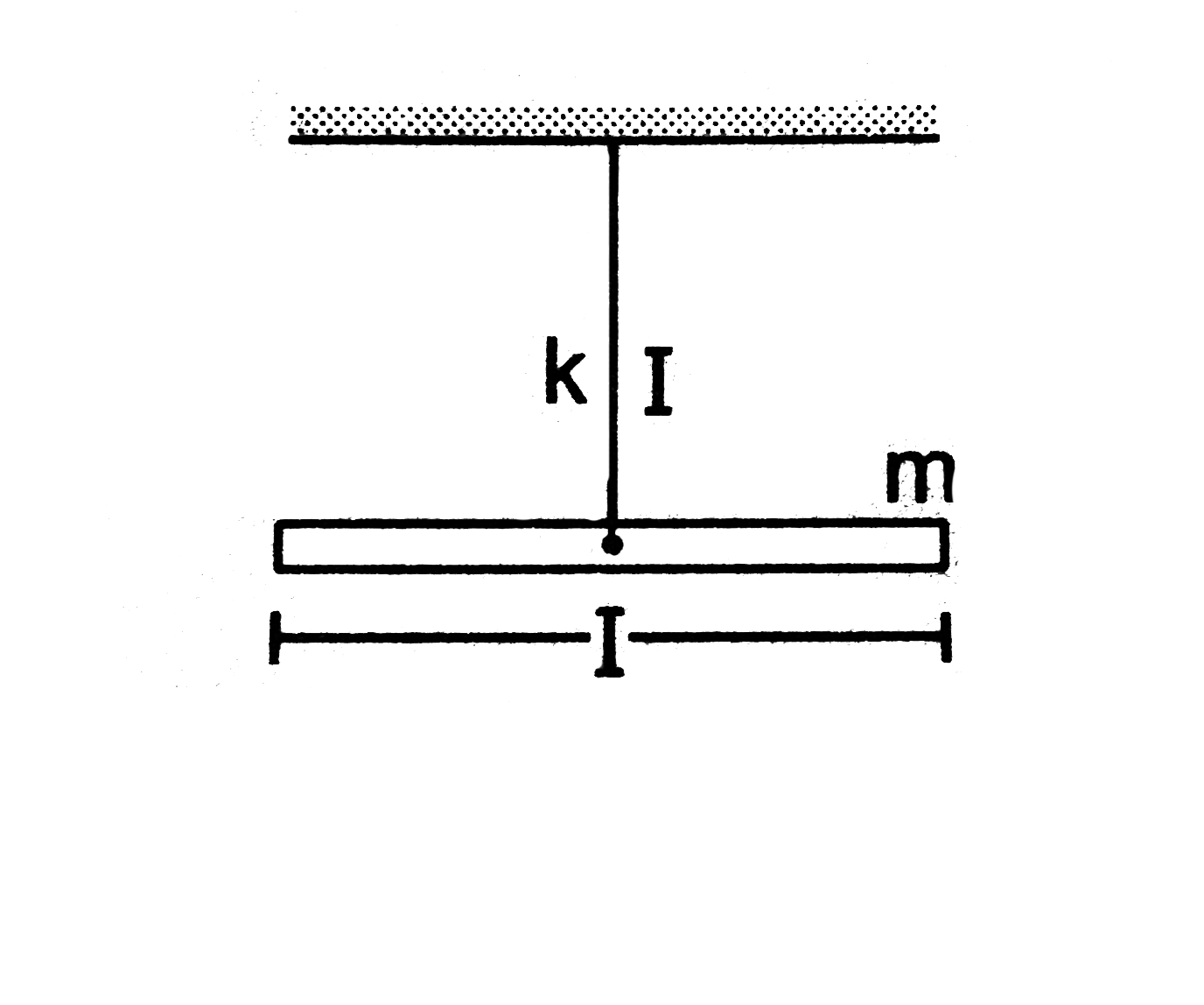
A uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
View SolutionA uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionA uniform rod of length l is suspended from a point P. and the rod is made to undergo small oxcillations. Match the following
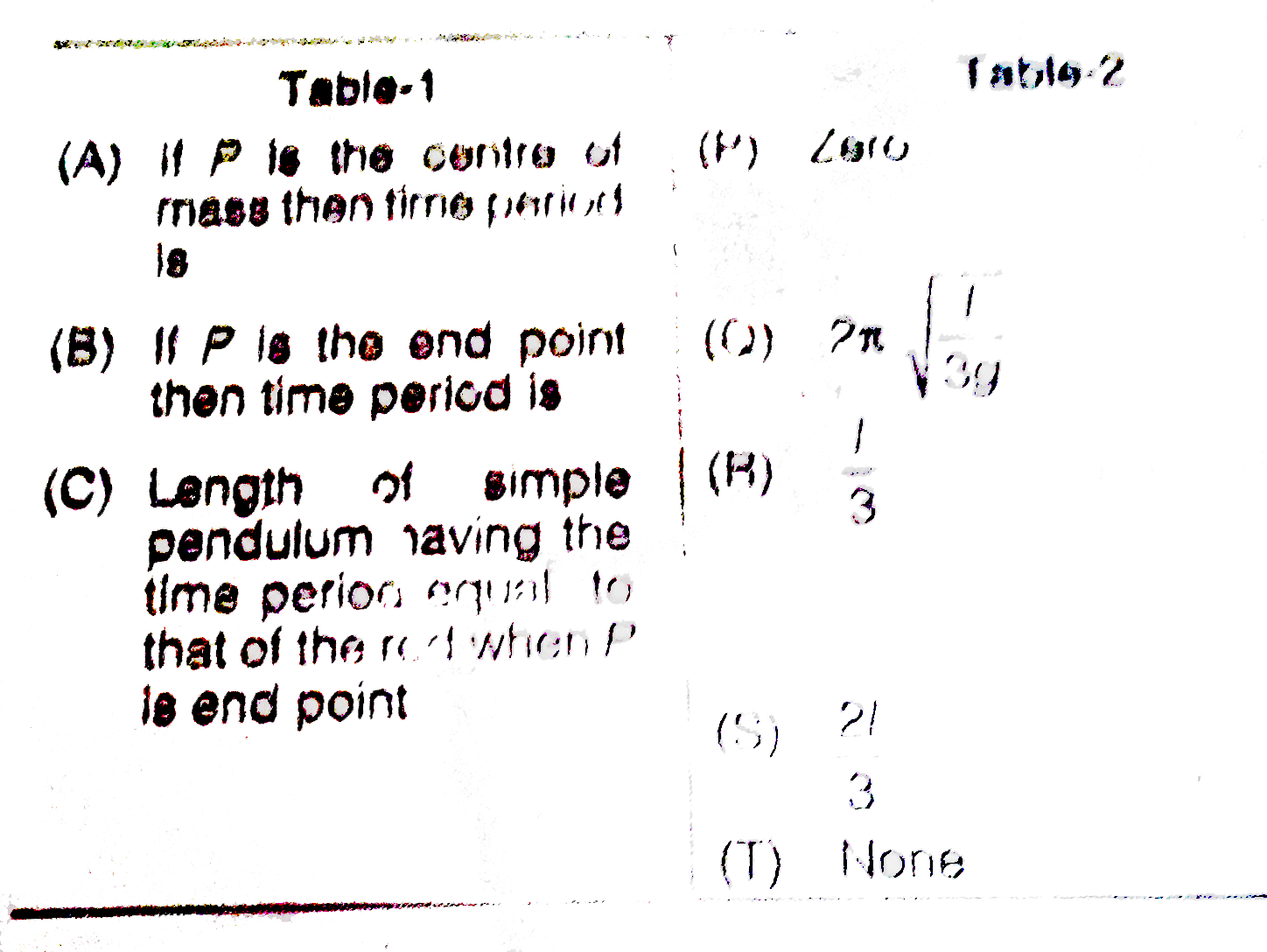
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View Solution
