For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
The period of oscillation
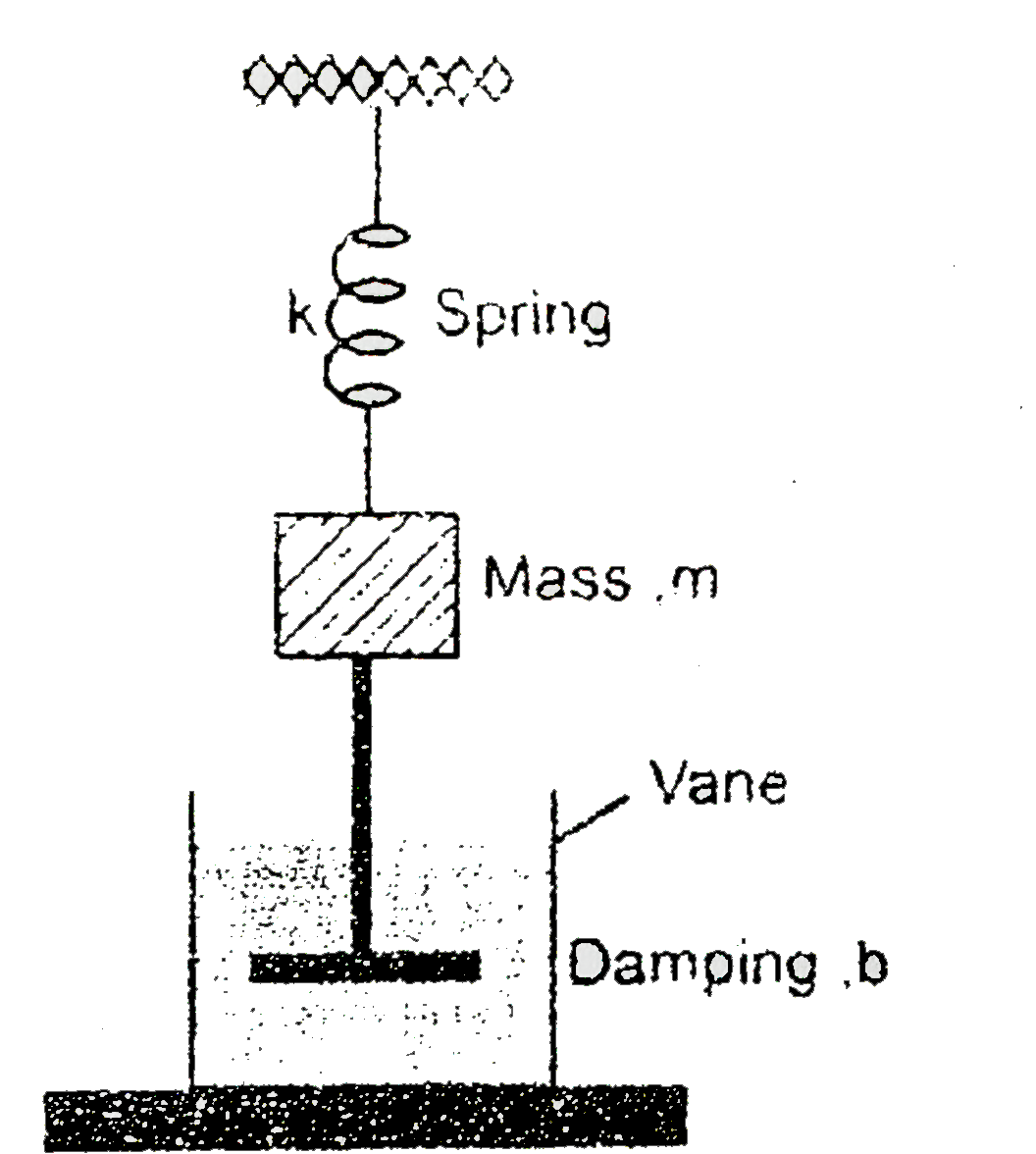
The correct Answer is:(a) 0.3s , (b) 6.93s , (c) 3.4s
(a) As the damping constant, b
(=0.04kgs−1)<<√km
the time period T from the equation
ω'=√km−b24m2 is given by.
T=2π√mk=2π√0.2kg80Nm−1=0.314s
(b) From the equation x(t)=xmɵbt2m the time T1/2 for the amplitude to drop to drop to half of its initial value is
12=ɵ−bt1/22m
or loge2=bT1/22m
or 0.693=bT1/22m
or T1/2=0.693l×2×0.240×10−3=6.93s
(c) E(t)=E(0)e−bt1/2m,
12=e−bt1/2m,loge2=bt1/2m
t1/2=0.693×0.240×103=m3.4sec
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II
36 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I
26 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
For the damped oscillator shown in Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View Solution
Knowledge Check
A block of mass 200 g executing SHM under the influence of a spring of spring constant k=90Nm−1 and a damping constant b=40gs−1. The time elapsed for its amplitude to drop to half of its initial value is (Given, ln (1/2)=−0.693)
A7sB9sC4sD11s
For the damped oscillator shown in previous figure, k=180Nm−1 and the damping constant b is 40gs−1 .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than √km).
Hint :T=2π√mk
View Solution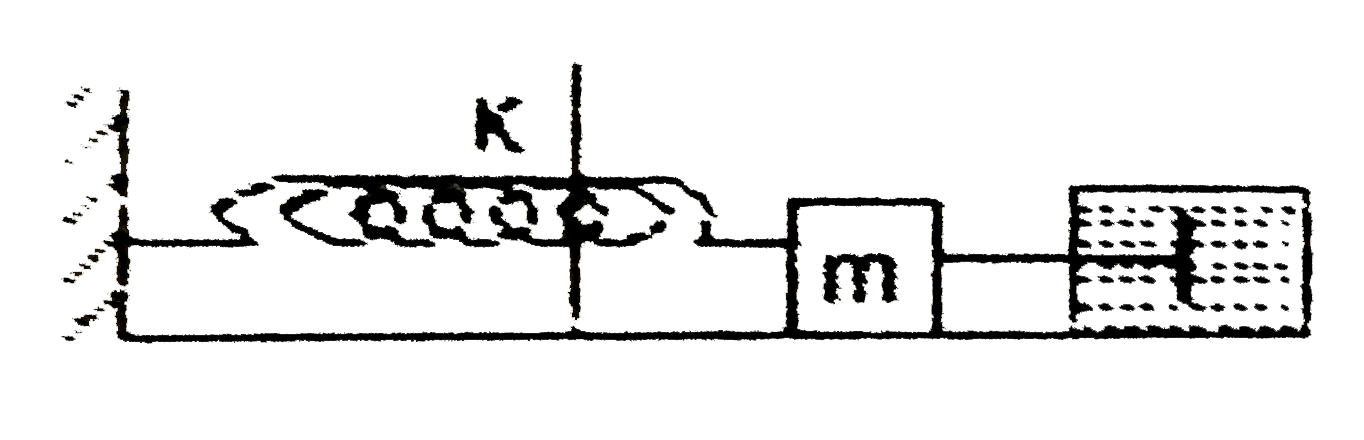
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.
View SolutionThe angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
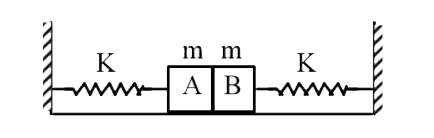
View SolutionTwo light spring of force constants k1 and k2 and a block of mass m are in one line AB on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance CD between the spring is 60cm. If the block moves along AB with a velocity 120cm/s in between the springs, calculate the period of oscillation of the block. (take k1=1.8N/m, k2=3.2N/m, m=200g)

View Solution
For the spring pendulum shown in fig. the value of spring constant is 3×104Nm and amplitude of oscillation is 0.1m. The total mechanical energy of oscillating system is 200 J. Mark out the correct option (s).
View Solution
A block of mass m is connected to a spring of spring constant k as shown in Fig. The block is found at its equilibrium position t=1s and it has a velocity of +0.25ms at t=2s. The time period of oscillation is 6 s. Based on the given information answer the following question: Q. the amplitude of oscillation is
View Solution
