Two apdulums begin to swing simultaneosuly. The first pendulum makes 9 full oscillations when the other makes 7. Find the ratio of length of the two pendulums
4981
79
5081
12
The correct Answer is:A
To solve the problem of finding the ratio of the lengths of two pendulums based on their oscillations, we can follow these steps:
1. Identify the Time Periods:
Let T1 be the time period of the first pendulum and T2 be the time period of the second pendulum.
2. Set Up the Relationship:
The first pendulum makes 9 oscillations while the second makes 7. Therefore, the total time taken for these oscillations can be expressed as:
9T1=7T2
3. Express Time Periods in Terms of Length:
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity. Thus, we can express T1 and T2 as:
T1=2π√L1gandT2=2π√L2g
4. Substitute Time Periods into the Relationship:
Substituting T1 and T2 into the equation from step 2 gives:
9(2π√L1g)=7(2π√L2g)
5. Cancel Common Terms:
The 2π and √g terms can be canceled from both sides:
9√L1=7√L2
6. Rearrange to Find the Ratio:
Rearranging gives:
√L1√L2=79
7. Square Both Sides:
Squaring both sides to eliminate the square roots results in:
L1L2=(79)2=4981
8. Final Answer:
The ratio of the lengths of the two pendulums is:
L1L2=4981
Let T1 be the time period of the first pendulum and T2 be the time period of the second pendulum.
The first pendulum makes 9 oscillations while the second makes 7. Therefore, the total time taken for these oscillations can be expressed as:
9T1=7T2
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity. Thus, we can express T1 and T2 as:
T1=2π√L1gandT2=2π√L2g
Substituting T1 and T2 into the equation from step 2 gives:
9(2π√L1g)=7(2π√L2g)
The 2π and √g terms can be canceled from both sides:
9√L1=7√L2
Rearranging gives:
√L1√L2=79
Squaring both sides to eliminate the square roots results in:
L1L2=(79)2=4981
The ratio of the lengths of the two pendulums is:
L1L2=4981
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I
26 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
Two pendulums differ in lengths by 22m. They oscillate at the same place so that one of then makes 30 oscillations and the other makes 36 oscillations during the same time. The length ( in cm) of the pendulum are :
View SolutionTwo simple pendulum with heavy bobs-one using iron wire and the other aluminimum wire are excited simultaneously. It is found that when the first pendulum completes 1000 oscillations the other completes 1001. When the temperature is raised by t∘C, it is found that the two pendulums now oscillate together. If he coefficients of thermal expansion of iron and aluminimum are 10×10−6/∘C and 30×10−6/∘C then the value of t is :
View Solution
Knowledge Check
Two pendulums differ in lengths by 22m. They oscillate at the same place so that one of then makes 30 oscillations and the other makes 36 oscillations during the same time. The length ( in cm) of the pendulum are :
A1. 72 and 50B2. 60 and 38C3. 50 and 28D4. 80 and 58Two pendulums differ in lengths by 22cm. They oscillate at the same place so that one of them makes 30 oscillations and the other makes 36 oscillations during the same time. The length ( in cm) of the pendulum are :
A72 and 50B60 and 38C50 and 28D80 and 58
Ratio of amplitude for two wave is 7:9 .Find the ratio of intensity?
View SolutionThe frequency of a simple pendulum is n oscillations per minute while that of another is (n+1) oscillations per minute. The ratio of length of first second is-
View SolutionTwo simple pendulums A and B are made to oscillate simultaneously and it is found that A completes 10 oscillations in 20s and B completed 8 oscillations in 10 s. The ratio of the length of A and B is
View Solution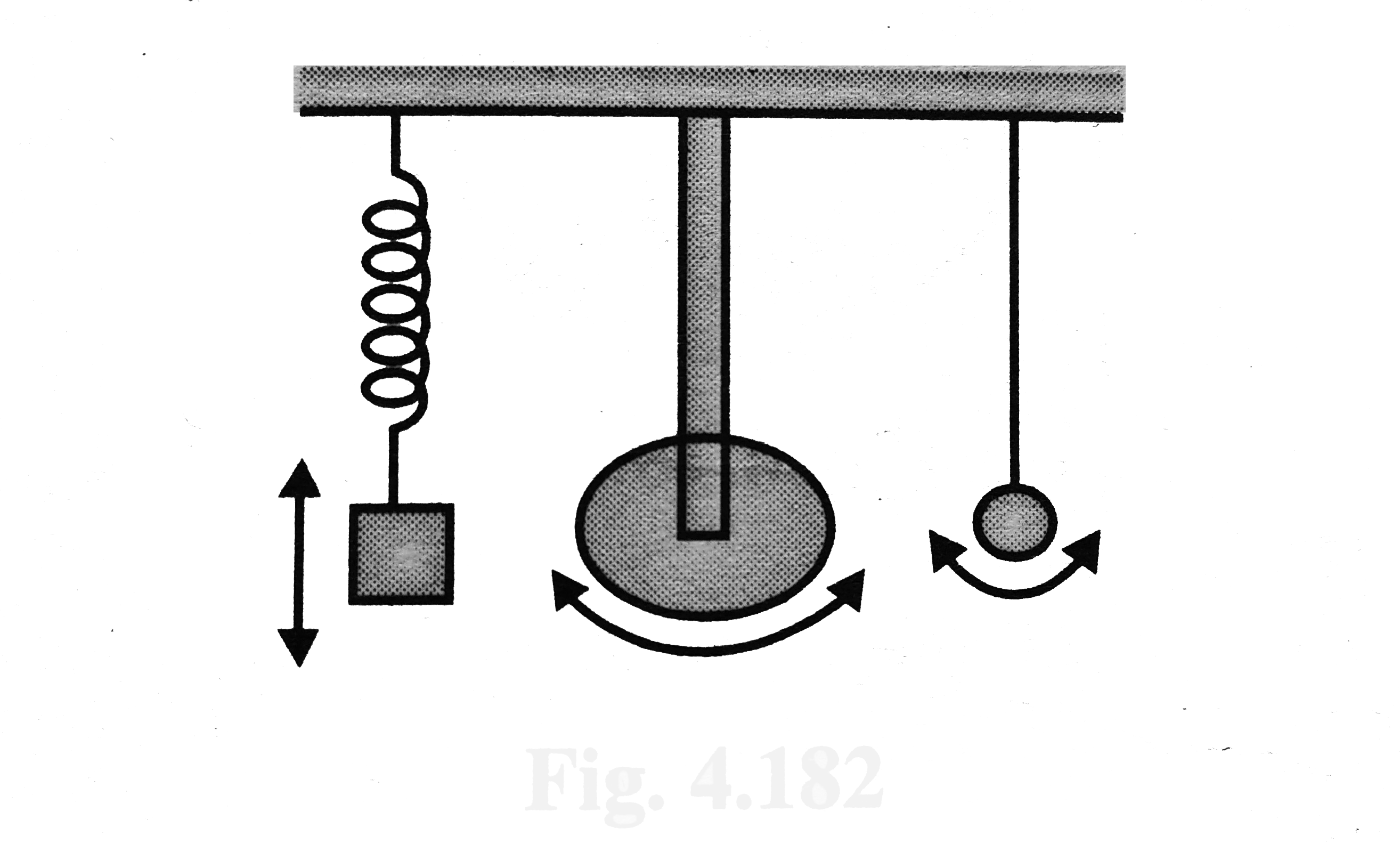
Q. Statement I Three pendulums are suspended from ceiling as shown in Fig. These three pendulums are set to oscillate as shon by arrows, and it is found that all three have same time period. Noe, all three are taken to a place where acceleration due to gravity changes to 4/9th of its value at the first place. If spring pendulum makes 60 cycles in a given time at this place, then torsion pendulum and simple pendulum will also make 60 oscillation in same (given) time interval. Statement II: Time period of torsion pendulum is independent of acceleration due to gravity.
View SolutionGeeta pours in equal amount of milk into two different vessels. One vessel is 47 th full and the other is 38 th full. Find the ratio of the volumes of the two vessels.
View SolutionThe diameter and density of a planet are twice that of the earth. Assuming the earth and the planet to be of uniform density, find the ratio of the lengths of two simple pendulums, of equal time periods, on the surface of the planet and the earth.
View Solution
