For a body executing SHM with amplitude A, time period T, maximum velocity vmax and phace constant zero, which of the following statements are correct for 0≤t≤T4 (y is displacement from mean position)?
At y=(A/2),v>(vmax/2)
for v=(vmax/2),y>(A/2)
For t=(T/8),(A/2)
For y=(A/2),t<(T/8)
The correct Answer is:A, B, C, D
To solve the question regarding a body executing Simple Harmonic Motion (SHM) with given parameters, we need to analyze the behavior of the displacement y as a function of time. The body has an amplitude A, time period T, maximum velocity vmax, and a phase constant of zero.
1. Understanding SHM Equation:
The displacement y of a body in SHM can be expressed as:
y(t)=Asin(2πTt)
where A is the amplitude and T is the time period.
2. Maximum Velocity:
The maximum velocity vmax in SHM is given by:
vmax=A⋅2πT
3. Displacement at Specific Time:
We need to evaluate the displacement y at t=T4:
y(T4)=Asin(2πT⋅T4)=Asin(π2)=A
Thus, at t=T4, the displacement is equal to the amplitude A.
4. Displacement at t=0:
At t=0, the displacement is:
y(0)=Asin(0)=0
5. Displacement at t=T2:
At t=T2:
y(T2)=Asin(2πT⋅T2)=Asin(π)=0
6. Summary of Displacement Values:
- At t=0, y=0
- At t=T4, y=A
- At t=T2, y=0
Conclusion:
From the analysis, we can conclude that:
- The displacement y reaches its maximum value A at t=T4.
- The displacement is zero at t=0 and t=T2.
The displacement y of a body in SHM can be expressed as:
y(t)=Asin(2πTt)
where A is the amplitude and T is the time period.
The maximum velocity vmax in SHM is given by:
vmax=A⋅2πT
We need to evaluate the displacement y at t=T4:
y(T4)=Asin(2πT⋅T4)=Asin(π2)=A
Thus, at t=T4, the displacement is equal to the amplitude A.
At t=0, the displacement is:
y(0)=Asin(0)=0
At t=T2:
y(T2)=Asin(2πT⋅T2)=Asin(π)=0
- At t=0, y=0
- At t=T4, y=A
- At t=T2, y=0
From the analysis, we can conclude that:
- The displacement y reaches its maximum value A at t=T4.
- The displacement is zero at t=0 and t=T2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV
8 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - I
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A particle is executing S.H.M. with amplitude A and has maximum velocity v0. Its speed at displacement 3A4 will be
View SolutionIf abody starts executing S.H.M. from mean position with amplitude 'A', maximum velocity v0 and time period 'T', then the correct statemens are (x is displacement from mean position)
View Solution
Knowledge Check
A particle executing SHM with time period T and amplitude A. The mean velocity of the particle averaged over quarter oscillation, is
AA4TB2ATC3ATD4AT
At particle is executing SHM with amplitude A and has maximum velocity v0. Find its speed when it is located at distance of A2 from mean position.
View SolutionA body is executing SHM with amplitude A and time period T. The ratio of kinetic and potential energy when displacement from the equilibrium position is half the amplitude
View SolutionThe displacement-time graph for a particle executing SHM is as shown in figure. Which of the following statements is correct?
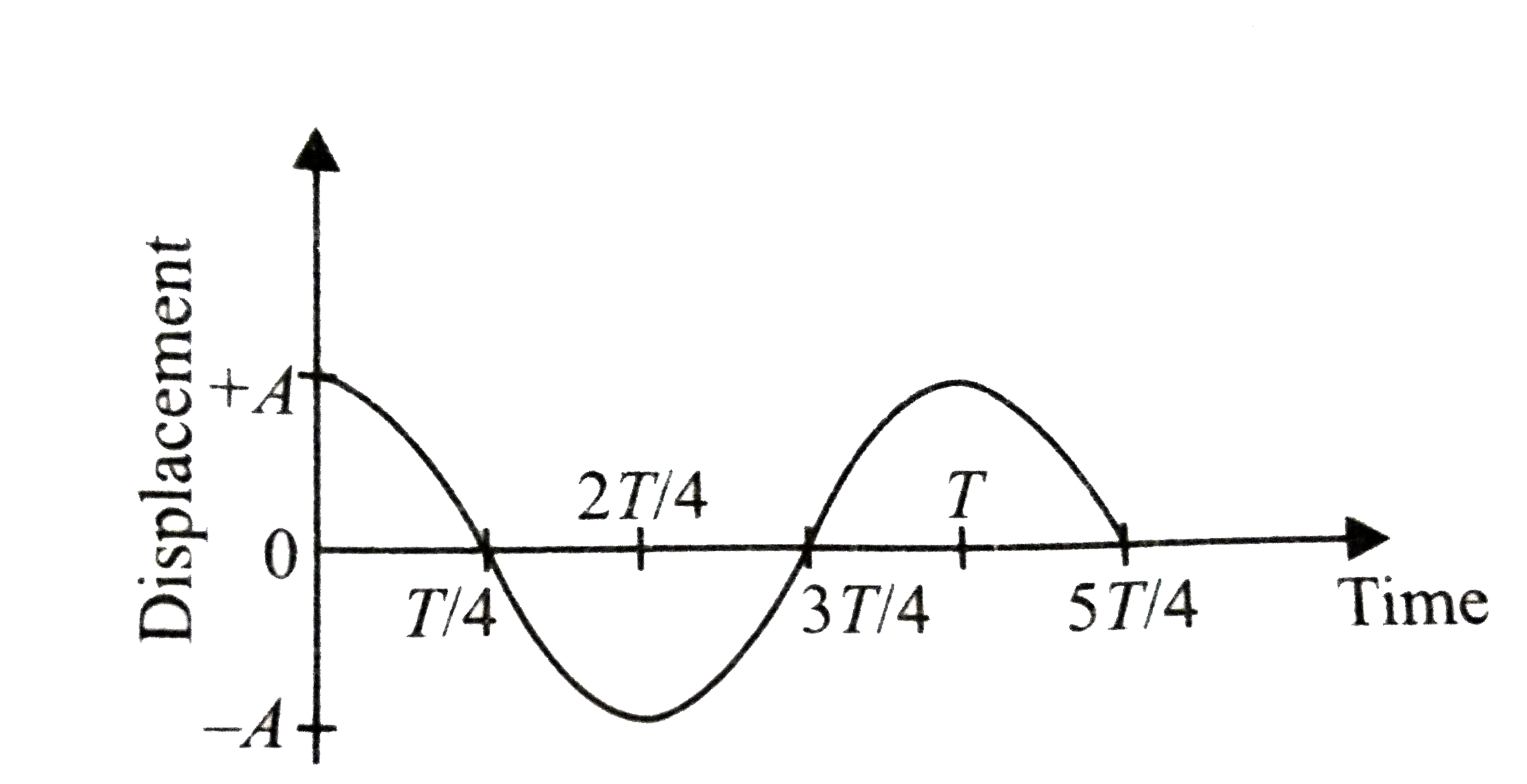
View SolutionIf y, v and a represent displacement velocity and acceleration at any instant for a particle executing SHM, which of the following statements are true?
View SolutionA body executes SHM with an amplitude a. At what displacement from the mean positions, the potentail energy of the body is one-fourth of its total energy?
View SolutionA particle executing SHM of amplitude a has displace ment a2 at t=T4 and a negative velocity. The epoch of the particle is
View SolutionA body is executing shm with an amplitude of 0.15 m and frequency 4. Hz. Compute (i) maximum velocity of the body (ii) acceleration when displacement is 0.09 m and time required to move from mean position to a point 0.12 m away from it.
View Solution
