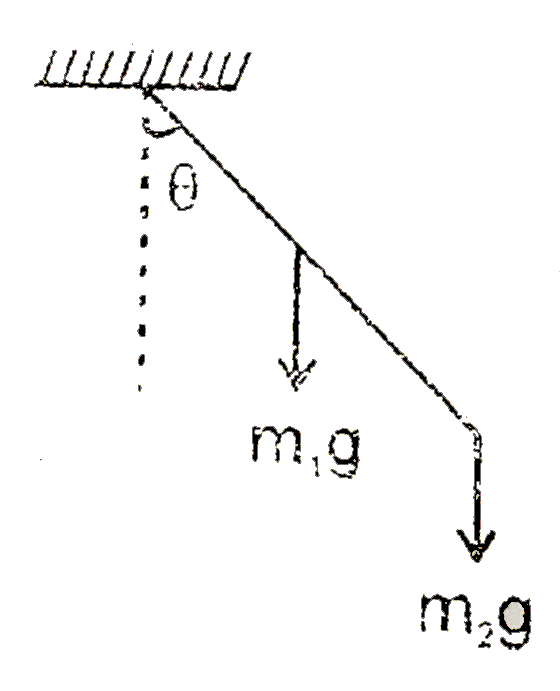
Two point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.
The correct Answer is:1
Net rostoring about O
=m1gl1sinθ+m2gl2sinθ=(m1l1+m2l2)gsinθ
⇒τrestoring=(m1l1+m2l2)gsinθ
compare with τ=Cθ
T=2π√IoC=2π
⎷(m1l21+m2l22)(m1l21+m2)g=1π.

Topper's Solved these Questions
Similar Questions
Block of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
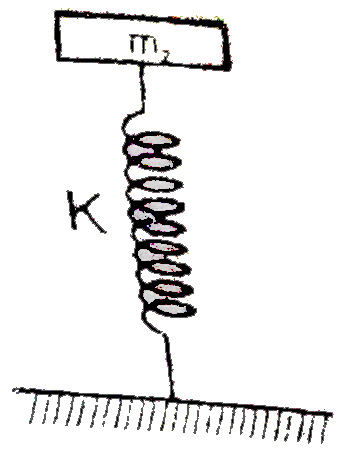 View Solution
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
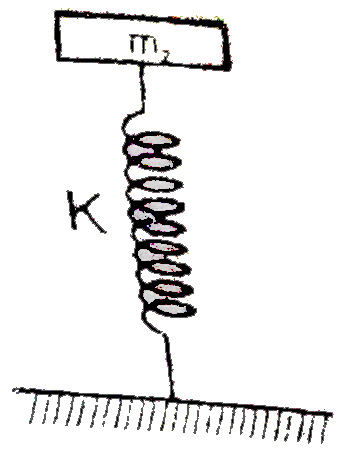 View Solution
View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.
 View Solution
View SolutionA uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
View SolutionTwo particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
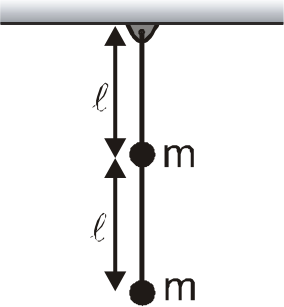 View Solution
View SolutionIf <l1,m1,n1>and<l2,m2,n2> be the direction cosines of two lines L1andL2 respectively. If the angle between them is θ, the cosθ=?
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
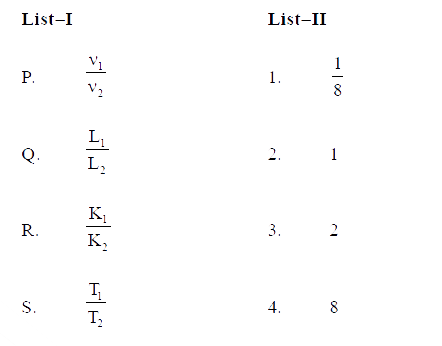 View Solution
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
 View Solution
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View Solution

