Derive an expression of wave velocity in terms of frequency and wavelength of the wave.
The correct Answer is:The velocity of transverse wave motion is given by
v=distancetravel≤dbythewavetimetaken
Since the distance equal to wavelength (λ) istrav-elled by the wave in a time equal to the period of vibration (T) of the particle of the medium, we have.
v=λT=(1T)λ
(reciprocal of time period is frequency)
v=vλ
To derive the expression for wave velocity in terms of frequency and wavelength, we can follow these steps:
Step 1: Understand the definitions
- Frequency (f) is defined as the number of waves that pass a point in one second. It is measured in Hertz (Hz).
- Wavelength (λ) is the distance between two consecutive points that are in phase on the wave, such as crest to crest or trough to trough.
Step 2: Relate frequency and time period
- The time period (T) is the time taken for one complete wave to pass a point. It is the reciprocal of frequency:
T=1f
Step 3: Define wave velocity
- The wave velocity (v) is the distance traveled by a wave in a unit of time. For one complete wave, the distance traveled is the wavelength (λ), and the time taken is the time period (T):
v=DistanceTime=λT
Step 4: Substitute the time period with frequency
- We already established that T=1f. Therefore, we can substitute T in the wave velocity equation:
v=λT=λ1f=λ⋅f
Step 5: Final expression
- Thus, the expression for wave velocity in terms of frequency and wavelength is:
v=λf
Summary
- The wave velocity (v) is equal to the product of the wavelength (λ) and the frequency (f):
v=λf
- Frequency (f) is defined as the number of waves that pass a point in one second. It is measured in Hertz (Hz).
- Wavelength (λ) is the distance between two consecutive points that are in phase on the wave, such as crest to crest or trough to trough.
- The time period (T) is the time taken for one complete wave to pass a point. It is the reciprocal of frequency:
T=1f
- The wave velocity (v) is the distance traveled by a wave in a unit of time. For one complete wave, the distance traveled is the wavelength (λ), and the time taken is the time period (T):
v=DistanceTime=λT
- We already established that T=1f. Therefore, we can substitute T in the wave velocity equation:
v=λT=λ1f=λ⋅f
- Thus, the expression for wave velocity in terms of frequency and wavelength is:
v=λf
- The wave velocity (v) is equal to the product of the wavelength (λ) and the frequency (f):
v=λf
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART I
23 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Solved Miscellaneous Problems
7 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART I
19 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
Knowledge Check
Figure given shows a sinusoidal wave on a string. If the frequency of the wave is 150 Hz, what is the velocity and wavelength of the given wave?
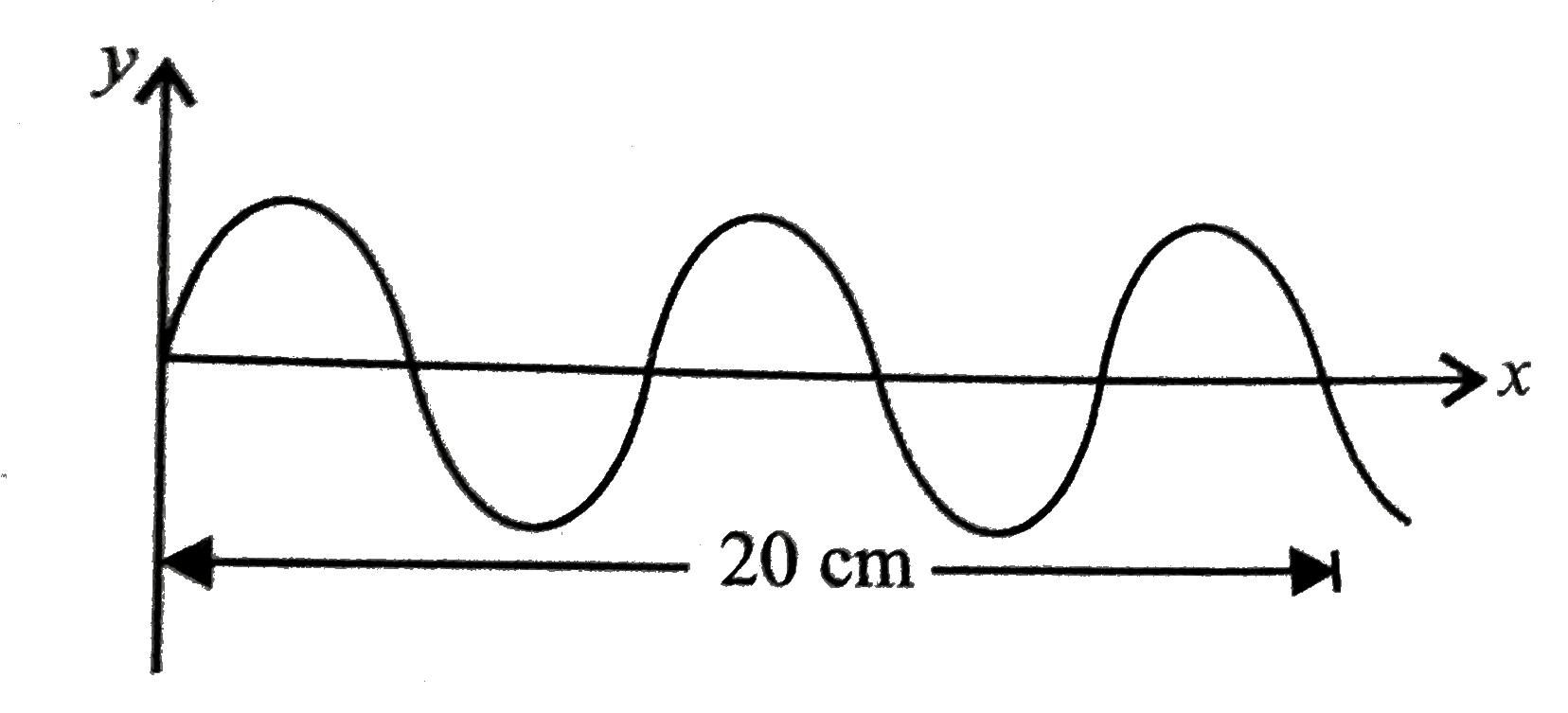 A0.04m,10ms−1B0.06m,12ms−1C0.08m,10ms−1D0.08m,12ms−1
A0.04m,10ms−1B0.06m,12ms−1C0.08m,10ms−1D0.08m,12ms−1
How are the wave velocity v, frequency n and wavelength λ of a wave related? Derive the relationship.
View SolutionHow are the wave velocity V, frequency f and wavelength λ of a wave related ? Derive the relationship.
View SolutionA standing wave arises on a string when two waves of equal amplitude , frequency and wavelength travelling in opposite superimose. If the frequency of oscillation of the standing waves
View SolutionOcean waves of time period 10 s have wave velocity 15 ms−1. Find the wavelength of these waves .
View SolutionThe diagram below shows (a) displacement-time, and (b) displacement-distance, graph of a wave travelling in a string with velocity 20 m s−1. In each case, use the graph to calculate the frequency and wavelength of the wave.
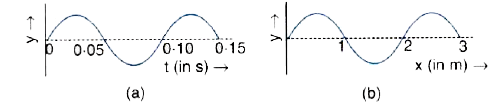
View SolutionEquation of a transverse wave travelling in a rope is given by
y=5sin(4.0t−0.02x)
where y and x are expressed in cm and time in seconds. Calculate
(a) the amplitude, frequency,velocity and wavelength of the wave.
(b) the maximum transverse speed and acceleration of a particle in the rope.
View SolutionSpeed of sound wave is v. If a reflector moves towards a stationary source emitting waves of frequency f with speed u, the wavelength of reflected waves will be
View Solution
