Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none at all y=2cos(3x)sin(10t)
The correct Answer is:(a) Stationary wave.
(b) Unacceptable funcation for any wave.
(c) Travelling harmonic wave.
(d) Superposition of two stationary waves.
To determine the type of wave represented by the given function y=2cos(3x)sin(10t), we will analyze its structure step by step.
Step 1: Identify the form of the wave equation
The general forms of wave equations are:
- Traveling Wave: y=Asin(ωt−kx) or y=Acos(ωt−kx)
- Stationary Wave: y=Acos(kx)sin(ωt)
Step 2: Analyze the given equation
The given equation is:
y=2cos(3x)sin(10t)
Step 3: Compare with the standard forms
In the equation y=2cos(3x)sin(10t):
- The term cos(3x) depends only on x.
- The term sin(10t) depends only on t.
This means that the equation is a product of two functions, one depending solely on position x and the other depending solely on time t.
Step 4: Conclusion
Since the equation can be expressed as a product of two separate functions (one in x and one in t), it matches the form of a stationary wave.
Thus, the function y=2cos(3x)sin(10t) represents a stationary wave.
Final Answer
- (i) Traveling wave: None
- (ii) Stationary wave: y=2cos(3x)sin(10t)
- (iii) None at all: None
---
The general forms of wave equations are:
- Traveling Wave: y=Asin(ωt−kx) or y=Acos(ωt−kx)
- Stationary Wave: y=Acos(kx)sin(ωt)
The given equation is:
y=2cos(3x)sin(10t)
In the equation y=2cos(3x)sin(10t):
- The term cos(3x) depends only on x.
- The term sin(10t) depends only on t.
Since the equation can be expressed as a product of two separate functions (one in x and one in t), it matches the form of a stationary wave.
- (i) Traveling wave: None
- (ii) Stationary wave: y=2cos(3x)sin(10t)
- (iii) None at all: None
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART I
23 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Solved Miscellaneous Problems
7 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART I
19 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none at all?
(a) y=2cos(3x)sin(10t) (b) y=2√x−vt
(c) y=3sin(5x−0.5t)+4cos(5x−0.5t) (d) y=cosxsint+cos2xsin2t
View SolutionGiven below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none at all?
(a) y=2cos(3x)sin(10t) (b) y=2√x−vt
(c) y=3sin(5x−0.5t)+4cos(5x−0.5t) (d) y=cosxsint+cos2xsin2t
View SolutionGiven below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none at all?
(a) y=2cos(3x)sin(10t)
(b) y=3sin(5x−0.5t)+4cos(5x−0.5t) (c) y=cosxsint+cos2xsin2t
View Solutionwhich of the following function corrtly represent the traveling wave equation for finite values of x and t ?
View Solutionwhich of the following function corrtly represent the traveling wave equation for finite values of x and t ?
View SolutionGive below are some functions of x and t to represent the displacement of an elastic wave.
(i)y=5cos(4x)sin(20t)
(ii) y=4sin(5x−t/2)+3cos(5x−t/2)
(iii) y=10cos[(252−250)πt]cos[(252+250πt] (iv)y=100cos(100πt+0.5x)
State which of these represent
(a) a travelling wave along-x direction
(b) a stationary wave
(c) beats
(d) a travelling wave along +x direction
Give reasons for your answers.
View Solution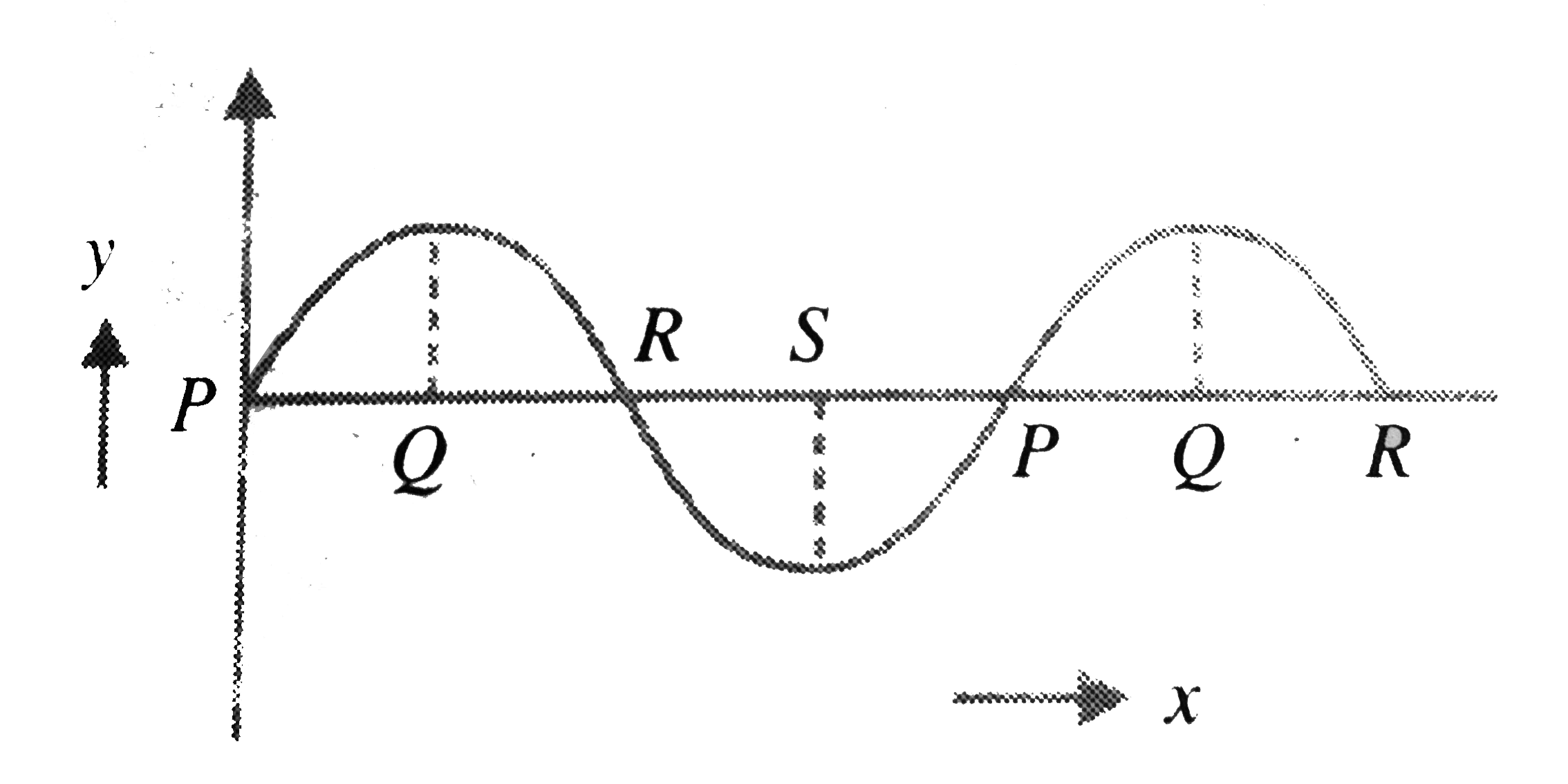
Figure. Represents the displacement y versus distance x along the direction of propagation of a longitudinal wave. The pressure is maximum at position marked
View SolutionThe transverse displamcement y(x,t) of a wave y(x,t ) on a string is given by yox, t) = . This represents a
View SolutionWhich of the following equations represent a transverse wave travelling along- y axis ?
View SolutionDoes a travelling wave in one dimension represented by a function of a linear combination of x and t,i.e., y=f(ax±bt) represented a travelling wave?
View Solution
