Question

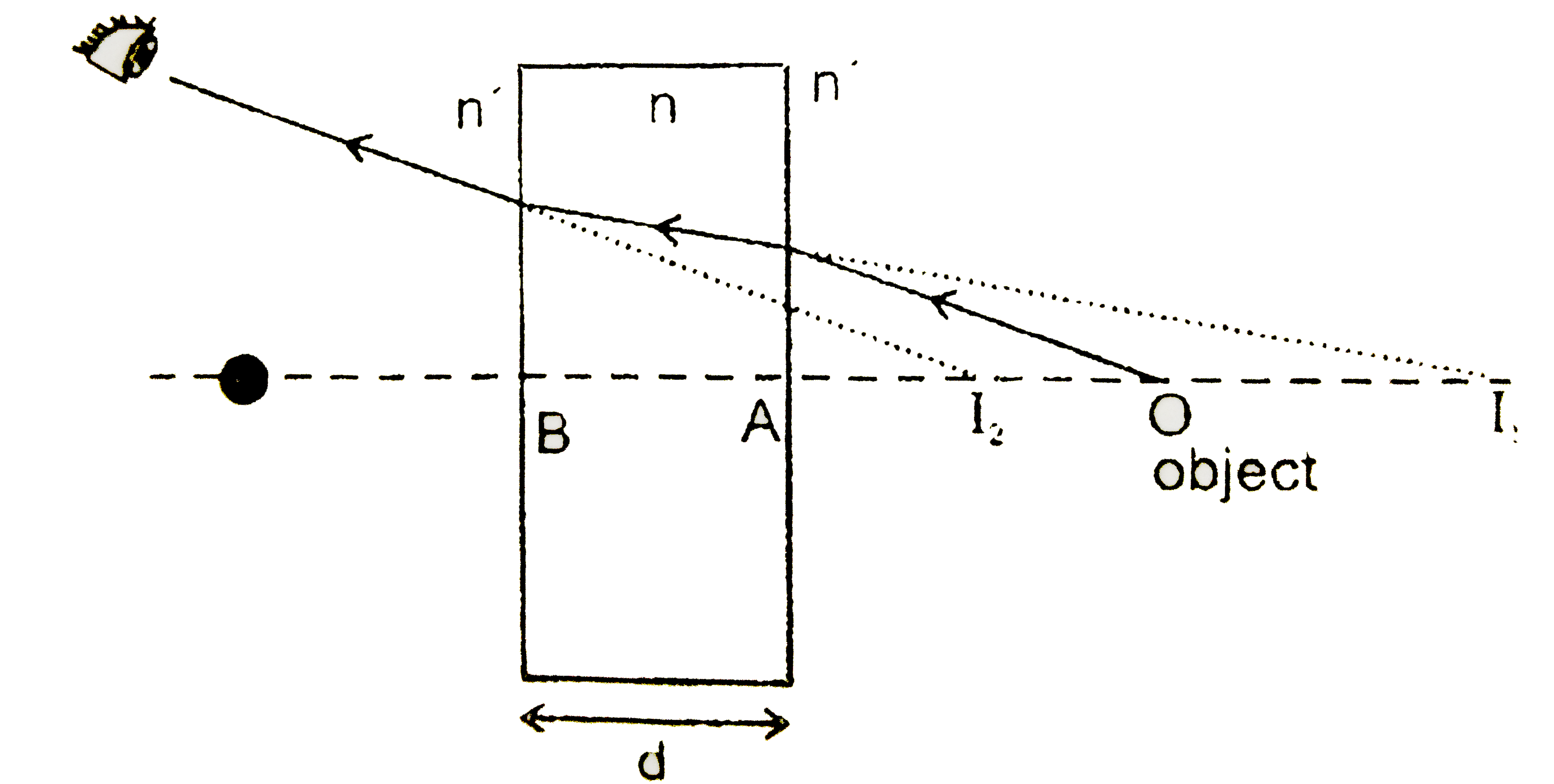
Prove that the shift in position of object due to parallel slab is given by shift
$=d(1-\frac{1}{n_{\text{net}}})$ where $n_{\text{rel}}=\frac{n}{n\text{'}}$

Explanation

Because of the way refraction at the first surface, the image of `O` is formed at `l_(1)`. For this refraction the real depth is `AO = x` and apparent depth is `AI_(1)`
Thus `Al_(1) = (AO)/(n_(i)//n_(r)) = (AO)/(n'//n) = (n(AO))/(n')`
The point `l_(1)` acts as the object for the refractin fo secound surface. Dua to this refraction, the image pf `l_(1)` is formed at `l_(2)` Thus,
`Bl_(2) = ((Bl_(1)))/((n//n')) = (n')/(n) (bl_(1))`
`= n'//n [d + (n)/(n') (AO)] = (n')/(n)d + AO`.
Net shift `= Oi_(2) = BO-Bl_(2)`
`= d + (AO) - (n')/(n)d - AO = d(1 - (n')/(n)) = d (1 - (1)/(n_("rel")))` where `n_("rel") = (n)/(n')`