A lens behaves as a converging lens in air and a diverging lens in water. The refractive index of the material is (refractive index of water =1.33)
equal to unity
equal to 1.33
between unity and 1.33
greater than 1.33
The correct Answer is:C
To solve the problem, we will use the lens maker's formula, which relates the focal length of a lens to its refractive index and the radii of curvature of its surfaces. The formula is given by:
1f=(μLμM−1)(1R1−1R2)
Where:
- f = focal length of the lens
- μL = refractive index of the lens
- μM = refractive index of the medium
- R1 and R2 = radii of curvature of the lens surfaces
1. Condition in Air (Converging Lens):
- In air, the refractive index μM=1.
- The lens behaves as a converging lens, so the focal length f is positive.
- Using the lens maker's formula:
1f=(μL−1)(1R1−1R2)(Equation 1)
2. Condition in Water (Diverging Lens):
- In water, the refractive index μM=1.33.
- The lens behaves as a diverging lens, so the focal length f is negative.
- Using the lens maker's formula:
1f=(μL1.33−1)(1R1−1R2)(Equation 2)
3. Setting Up the Equations:
- From Equation 1:
1f=(μL−1)(1R1−1R2)
- From Equation 2:
−1f=(μL1.33−1)(1R1−1R2)
4. Equating the Two Expressions:
- Set the two expressions for 1f equal to each other:
(μL−1)(1R1−1R2)=−(μL1.33−1)(1R1−1R2)
- Let x=(1R1−1R2):
(μL−1)x=−(μL1.33−1)x
- Assuming x≠0 (since the lens has curvature), we can divide both sides by x:
μL−1=−(μL1.33−1)
5. Solving for μL:
- Rearranging gives:
μL−1=−μL1.33+1
- Combine like terms:
μL+μL1.33=2
- Factor out μL:
μL(1+11.33)=2
- Calculate 1+11.33:
1+11.33=1.33+11.33=2.331.33
- Thus:
μL⋅2.331.33=2
- Solving for μL:
μL=2⋅1.332.33≈1.14
Final Answer:
The refractive index of the lens material is approximately μL≈1.14.
- f = focal length of the lens
- μL = refractive index of the lens
- μM = refractive index of the medium
- R1 and R2 = radii of curvature of the lens surfaces
- In air, the refractive index μM=1.
- The lens behaves as a converging lens, so the focal length f is positive.
- Using the lens maker's formula:
1f=(μL−1)(1R1−1R2)(Equation 1)
- In water, the refractive index μM=1.33.
- The lens behaves as a diverging lens, so the focal length f is negative.
- Using the lens maker's formula:
1f=(μL1.33−1)(1R1−1R2)(Equation 2)
- From Equation 1:
1f=(μL−1)(1R1−1R2)
- From Equation 2:
−1f=(μL1.33−1)(1R1−1R2)
- Set the two expressions for 1f equal to each other:
(μL−1)(1R1−1R2)=−(μL1.33−1)(1R1−1R2)
- Let x=(1R1−1R2):
(μL−1)x=−(μL1.33−1)x
- Assuming x≠0 (since the lens has curvature), we can divide both sides by x:
μL−1=−(μL1.33−1)
- Rearranging gives:
μL−1=−μL1.33+1
- Combine like terms:
μL+μL1.33=2
- Factor out μL:
μL(1+11.33)=2
- Calculate 1+11.33:
1+11.33=1.33+11.33=2.331.33
- Thus:
μL⋅2.331.33=2
- Solving for μL:
μL=2⋅1.332.33≈1.14
The refractive index of the lens material is approximately μL≈1.14.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
80 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
(i) If f=+0.5m, what is the power of the lens ?
(ii) The radii of curvature of the faces of a double convex lens are 9cmand15cm. Its focal length is 12cm. What is the refractive index of glass ?
(iii) A convex lens has 20cm focal length in air. What is the focal length in water ? (Refractive index of air-water =1.33, refractive index of air-glass =1.5).
View SolutionCalculate the critical angle of glass and water pair. (The refractive index for glass is 1.50 and refractive index for water is 1.33).
View SolutionA plano convex lens has radius of curvature 10 cm. Its focal length is 80 cm under water. Calculate the refractive index of the material of the lens, given refractive index of water is 4/3.
View SolutionAn equiconcave diverging lens of focal length F is cut into two equal halves. The two halves are turned around and joined with some liquid between them.The lens obtained is converging with focal length F. If the refractive index of the liquid is 3 then what is the refractive index of the lens?
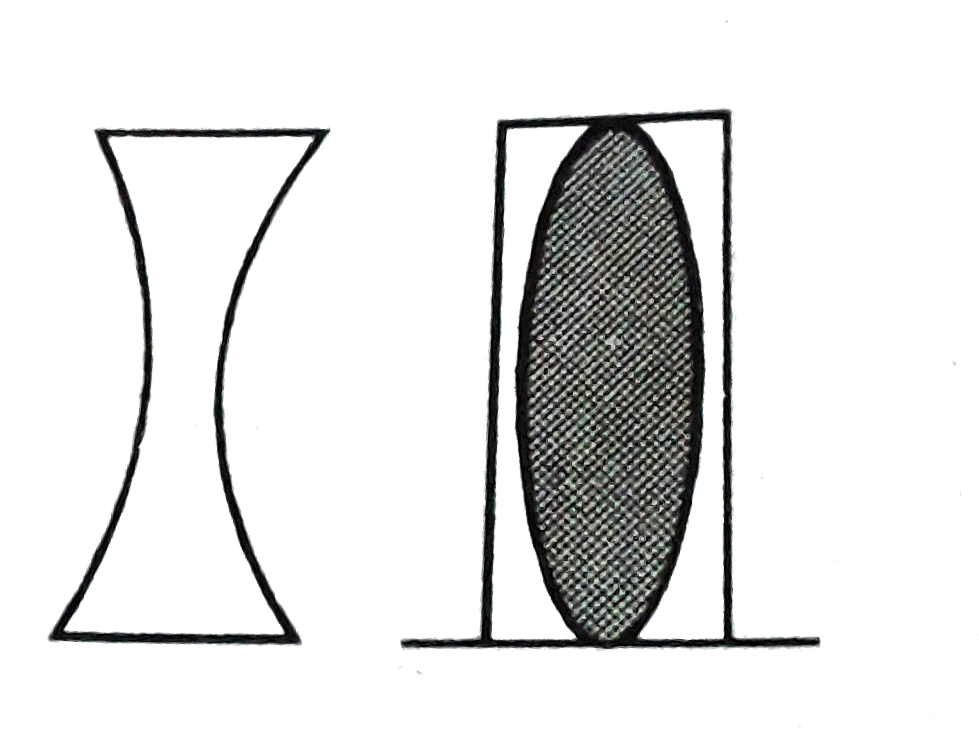
View SolutionA converging lens has a focal length of 20cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, what will be its new foacl length ?
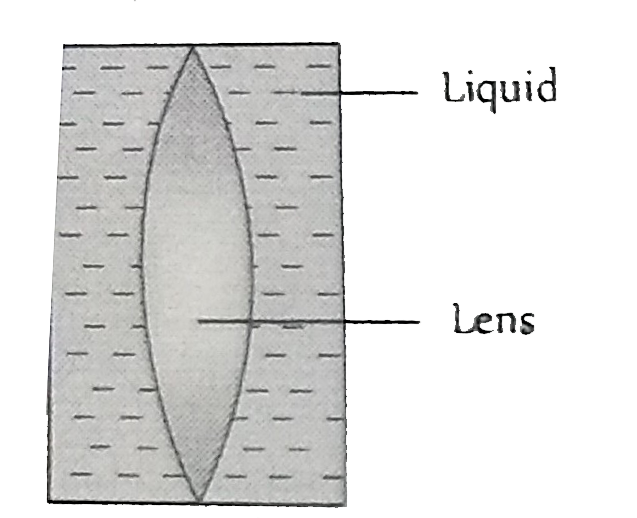
View SolutionShown in the figure here is a convergent lens placed inside a cell filled with a liquid. The lens has focal length +20cm when in air and its material has refractive index 1.50. If the liquid has refractive index 1.60, the focal length of the system is
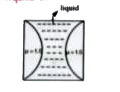
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
View SolutionThe refractive index of water is 1.33. What will be the speed of light in water
View SolutionThe focal length of an equi-concave lens is 34 times of radius of curvature of its surfaces. Find the refractive index of the material of lens. Under what condition will this lens behave as a converging lens?
View SolutionThe given figure shows a convergent lens placed inside a cell filled with liquid. The lens has focal length +20 cm when in air , and its metrial has refractive index 1.50 . If the liquid has refractive index 1.60 , then focal length of the lens in the cell is
View Solution
