Choose the correct alternative corresponding to the object distance 'u', image distance 'v' and the focal length 'F' of a converging lens from the following .
(i) The average speed of the image as the object moves with the uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with same speed from distance F2toF4
(ii) The minimum distance between a real object and its real image in case of a converging lens is 4F where F is its focal length.
both are correct
both are incorrect
(i) is correct , (ii) is incorrect
(i) is incorrect , (ii) is correct
The correct Answer is:B,C
To solve the problem, we need to analyze the two statements provided regarding the behavior of a converging lens.
Step 1: Analyze Statement (i)
Statement (i): The average speed of the image as the object moves with uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with the same speed from distance F2 to F4.
1. Using the Lens Formula:
The lens formula is given by:
1v−1u=1f
Where v is the image distance, u is the object distance, and f is the focal length.
2. Calculate Image Distance for the First Case:
- For u=−3F4:
1v1=1f+43F
- Solving gives:
v1=3F1=3F
- For u=−F2:
1v2=1f+2F
- Solving gives:
v2=2F
3. Calculate Average Speed:
- The average speed of the image when the object moves from 3F4 to F2:
Distance covered=v1−v2=3F−2F=F
- Time taken:
t1=DistanceSpeed=Fα0
- Average speed:
Average speed1=Ft1=FFα0=α0
- For the second case from F2 to F4:
- Calculate v for both positions similarly and find the average speed.
4. Comparison:
- After calculating both average speeds, we find that the average speed from 3F4 to F2 is indeed greater than from F2 to F4.
Conclusion for Statement (i):
The statement is true.
---
Step 2: Analyze Statement (ii)
Statement (ii): The minimum distance between a real object and its real image in case of a converging lens is 4F.
1. Using the Lens Formula Again:
- The total distance x between the object and the image is given by:
x=u+v
2. Find Minimum Distance:
- From the lens formula, we know:
v=u⋅fu+f
- Substitute v into x:
x=u+u⋅fu+f
- Differentiate x with respect to u and set it to zero to find the minimum.
3. Calculate Minimum:
- After differentiation and solving, we find u=2f.
- Substitute u back to find v:
v=2f
- Therefore, the minimum distance x=u+v=2f+2f=4f.
Conclusion for Statement (ii):
The statement is true.
---
Final Answer:
Both statements are true.
The lens formula is given by:
1v−1u=1f
Where v is the image distance, u is the object distance, and f is the focal length.
- For u=−3F4:
1v1=1f+43F
- Solving gives:
v1=3F1=3F
1v2=1f+2F
- Solving gives:
v2=2F
- The average speed of the image when the object moves from 3F4 to F2:
Distance covered=v1−v2=3F−2F=F
- Time taken:
t1=DistanceSpeed=Fα0
- Average speed:
Average speed1=Ft1=FFα0=α0
- Calculate v for both positions similarly and find the average speed.
- After calculating both average speeds, we find that the average speed from 3F4 to F2 is indeed greater than from F2 to F4.
The statement is true.
- The total distance x between the object and the image is given by:
x=u+v
- From the lens formula, we know:
v=u⋅fu+f
- Substitute v into x:
x=u+u⋅fu+f
- Differentiate x with respect to u and set it to zero to find the minimum.
- After differentiation and solving, we find u=2f.
- Substitute u back to find v:
v=2f
- Therefore, the minimum distance x=u+v=2f+2f=4f.
The statement is true.
Both statements are true.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]
23 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 01
45 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Choose the correct alternative corresponding to the object distance 'u', image distance 'v' and the focal length 'F' of a converging lens from the following .
(i) The average speed of the image as the object moves with the uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with same speed from distance F2toF4
(ii) The minimum distance between a real object and its real image in case of a converging lens is 4F where F is its focal length.
View SolutionThe minimum distance between a real object and its real image formed by a thin converging lens of focal length f is
View SolutionThe minimum distance between an object and its real image formed by a thin convex lens of focal length f is K.f. Find the value of K.
View SolutionThe distance between an object and its doubly magnified image by a concave mirror is: [Assume f= focal length]
View SolutionAn object is placed at a distance f in front of a concave lens of focal length f. Locate its image.
View Solution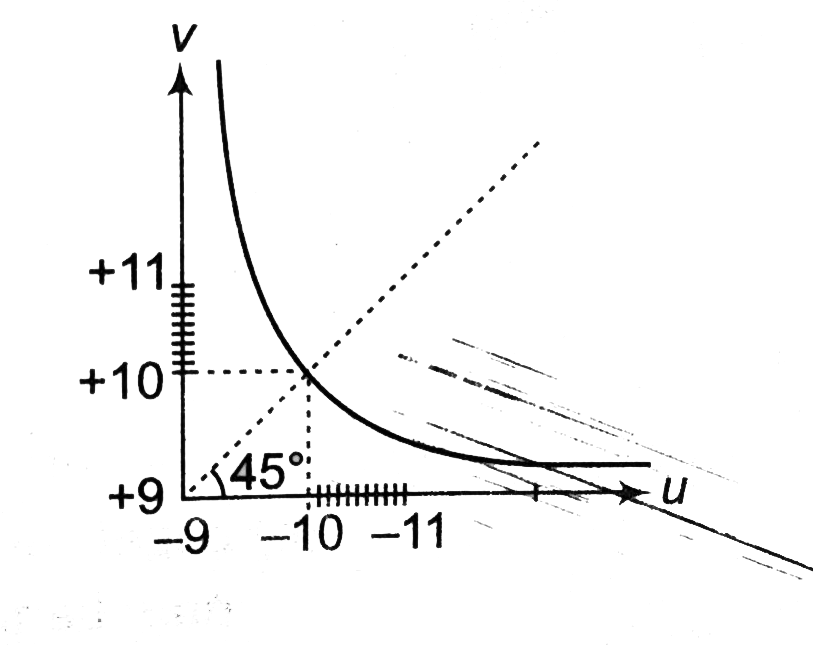 .
.
The graph between object distance u and image distance v from a convex lens is given .The correct option option , from the following ,is
View SolutionIf the distances of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
View SolutionIf the distances of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
View SolutionAn object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
View SolutionAs an object is moved from the surface of a thin converging lens to a focal point, over what range does the image distance very?
View Solution
