An equiconvex lens, with redii of curvature of magnitude 10cm each, is put over a liquid layer poured on top of a plane mirror. A small needle, with its tip on the principal axis of the lens, is moved along the axis until its inverted real image coincides with the needle itself. The distance of the needle, from the lens, is measured to be 15cm .
On removing the liquid layer, and repeating the experiment the distance is measured to be 10cm . Given that the two values of the distance measured represent the force length values in the two cases, calculate the refractive index of the liqiud.
To solve the problem, we will follow these steps:
Step 1: Understanding the Setup
We have an equiconvex lens placed over a liquid layer on a plane mirror. A small needle is placed on the principal axis of the lens. The distances measured when the liquid is present and when it is removed are given as 15 cm and 10 cm, respectively.
Step 2: Identifying Focal Lengths
1. With Liquid Layer:
- The distance measured (15 cm) corresponds to the focal length of the combination of the lens and the liquid. Let's denote this focal length as FL.
- Therefore, FL=15cm.
2. Without Liquid Layer:
- The distance measured (10 cm) corresponds to the focal length of the lens alone. Let's denote this focal length as FG.
- Therefore, FG=10cm.
Step 3: Using the Lens Maker's Formula
The lens maker's formula for the combination of two lenses (in this case, the lens and the liquid) is given by:
1F=1FG+1FL
Rearranging gives us:
1FL=1F−1FG
Step 4: Substitute Known Values
Substituting the known values into the equation:
1FL=115−110
Finding a common denominator (30):
1FL=230−330=−130
Thus, we find:
FL=−30cm
Step 5: Relating Focal Length to Refractive Index
For the plano-convex lens formed by the liquid, we can use the formula:
1FL=(n−1)(1R1−1R2)
Where:
- n is the refractive index of the liquid,
- R1 is the radius of curvature of the convex surface (10 cm),
- R2 is the radius of curvature of the plane surface (infinity).
Step 6: Substitute Values
Substituting the values:
1−30=(n−1)(110−0)
This simplifies to:
1−30=(n−1)110
Step 7: Solve for Refractive Index
Cross-multiplying gives:
−10=30(n−1)
Expanding and solving for n:
−10=30n−30
30n=20
n=2030=23+1=53≈1.33
Conclusion
The refractive index of the liquid is approximately n=1.33.
---
We have an equiconvex lens placed over a liquid layer on a plane mirror. A small needle is placed on the principal axis of the lens. The distances measured when the liquid is present and when it is removed are given as 15 cm and 10 cm, respectively.
1. With Liquid Layer:
- The distance measured (15 cm) corresponds to the focal length of the combination of the lens and the liquid. Let's denote this focal length as FL.
- Therefore, FL=15cm.
- The distance measured (10 cm) corresponds to the focal length of the lens alone. Let's denote this focal length as FG.
- Therefore, FG=10cm.
The lens maker's formula for the combination of two lenses (in this case, the lens and the liquid) is given by:
1F=1FG+1FL
Rearranging gives us:
1FL=1F−1FG
Substituting the known values into the equation:
1FL=115−110
Finding a common denominator (30):
1FL=230−330=−130
Thus, we find:
FL=−30cm
For the plano-convex lens formed by the liquid, we can use the formula:
1FL=(n−1)(1R1−1R2)
Where:
- n is the refractive index of the liquid,
- R1 is the radius of curvature of the convex surface (10 cm),
- R2 is the radius of curvature of the plane surface (infinity).
Substituting the values:
1−30=(n−1)(110−0)
This simplifies to:
1−30=(n−1)110
Cross-multiplying gives:
−10=30(n−1)
Expanding and solving for n:
−10=30n−30
30n=20
n=2030=23+1=53≈1.33
The refractive index of the liquid is approximately n=1.33.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
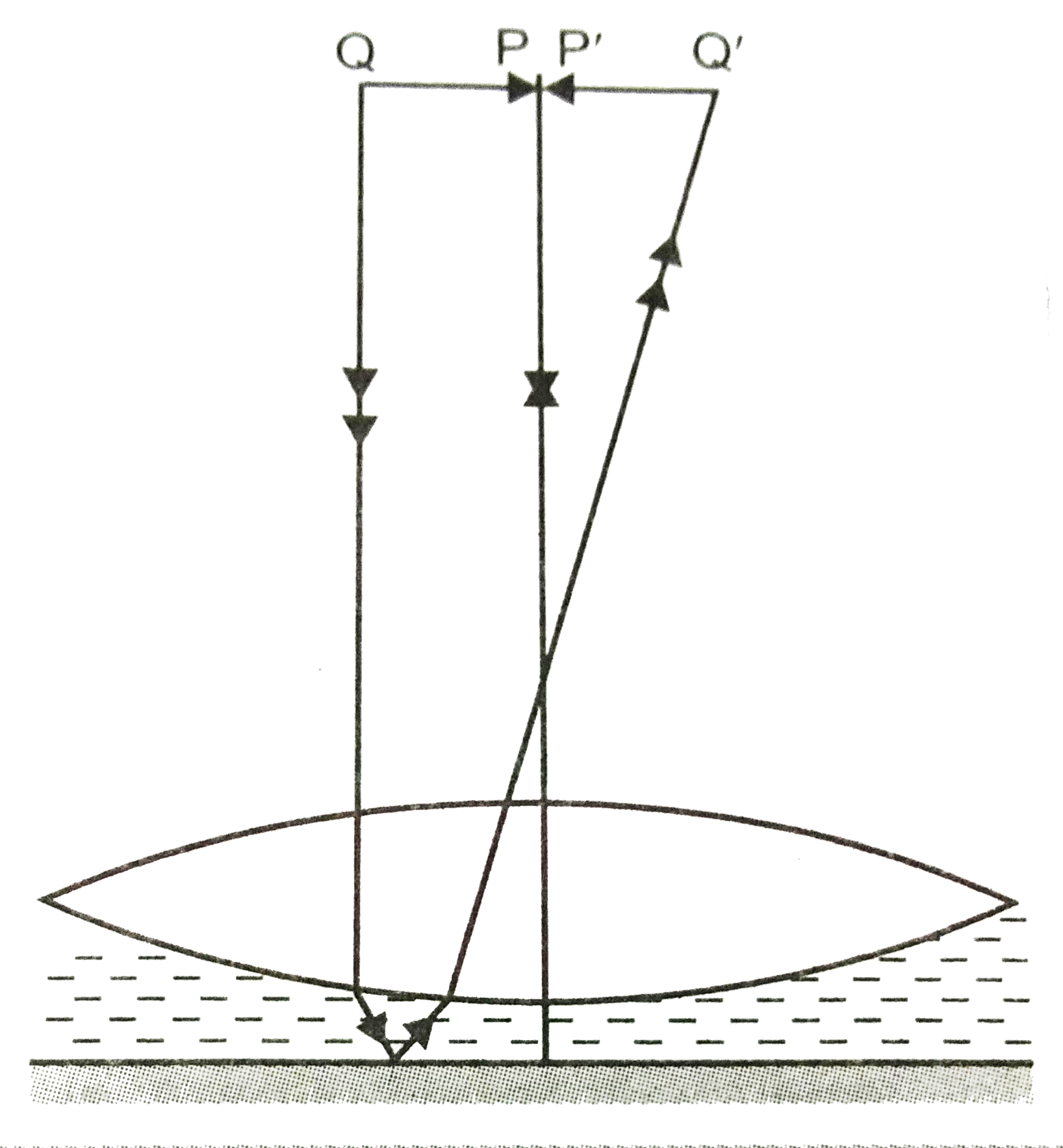
Fig. shows an equiconvex lens (of refractive index 1.5) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid ?
View SolutionA synunetdc bionvex fens of radius of curvature Rand made of glass of refractive index 1.5, is placed on a placed on top of a plane mirror as shown in the figure.An optical needle with with its tip on the principal axis of the lens is moved along the axis until its real, inverted images conicides with the needle itself. The distance from the lens in measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y . Obtain the expression for the refractive index of the liquid in terms of x and y.
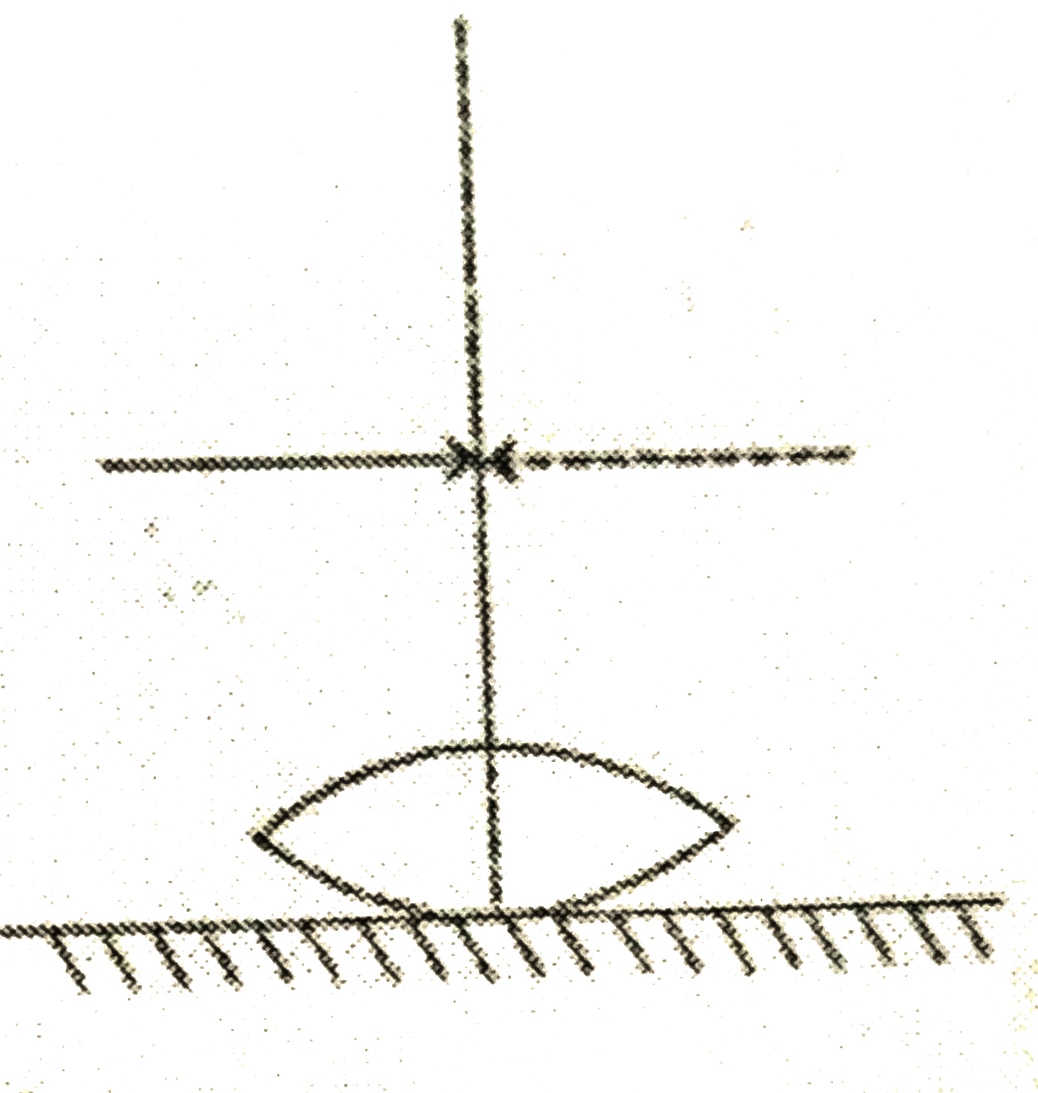
View SolutionA thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionAn object of length 2.0 cm is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. Find the size of the image of the object is at a distance of 8.0 cm from the lens.
View SolutionA thin rod of length (f3) is lying along the principal axis of a concave
mirror of focal length f.Image is real , magnified and inverted and one of the end or rod coincides with its image itself. Find length of the image.
View SolutionA point object moves along the principal axis of a convex lens of focal length f such that its real image, also formed on the principal axis at a distance 4f3 (at t=0) moves away from the lens with uniform velocity α. Find the velocity of the point object as a function of time t.
View SolutionPoint object O is placed on the principal axis of a convex lens of focal length 20cm at a distance of 40 cm to the left of it. The diameter of the lens is 10cm to the right of the lens at a distance h below the principal axis, then the maximum value of h to see the image will be
View SolutionA convex lens forms a real and inverted image of a needle at a distance of 50cm from it. Where is the needle placed in front of the convex lens if the image is equal to size of the object ? Also, find the power of the lens.
View SolutionA pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
View SolutionTwo point objects are placed on principal axis of a thin converging lens. One is 20cm from the lens and other is on the other side of lens at a distance of 40 cm from the lens. The images of both objects coincide. The magnitude of focal length of lens is :-
View Solution
