A glass lens of refractive index 1.5 is placed in a trough of liquid. What must be the refractive index of the liquid in order to mark the lens disappear?
To solve the problem of determining the refractive index of the liquid required for a glass lens (with a refractive index of 1.5) to become invisible, we can follow these steps:
1. Understanding the Concept:
- A lens appears to disappear when the light rays passing through it do not bend at the interface between the lens and the surrounding medium. This occurs when the refractive index of the lens is equal to that of the surrounding medium.
2. Identify the Given Information:
- Refractive index of the glass lens (μ_glass) = 1.5
- Refractive index of the liquid (μ_liquid) = ?
3. Condition for Disappearance:
- For the lens to disappear, the refractive index of the liquid must be equal to the refractive index of the glass lens. This means:
μliquid=μglass
4. Substituting the Known Values:
- Since we know that the refractive index of the glass lens is 1.5, we can write:
μliquid=1.5
5. Conclusion:
- Therefore, the refractive index of the liquid must be 1.5 for the lens to become invisible.
Final Answer:
The refractive index of the liquid must be 1.5.
---
- A lens appears to disappear when the light rays passing through it do not bend at the interface between the lens and the surrounding medium. This occurs when the refractive index of the lens is equal to that of the surrounding medium.
- Refractive index of the glass lens (μ_glass) = 1.5
- Refractive index of the liquid (μ_liquid) = ?
- For the lens to disappear, the refractive index of the liquid must be equal to the refractive index of the glass lens. This means:
μliquid=μglass
- Since we know that the refractive index of the glass lens is 1.5, we can write:
μliquid=1.5
- Therefore, the refractive index of the liquid must be 1.5 for the lens to become invisible.
The refractive index of the liquid must be 1.5.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
A converging lens of refractive index 1.5 is kept in a liquid medium having the same refractive index. What would be the focal length of the lens in the medium ?
View SolutionAn equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
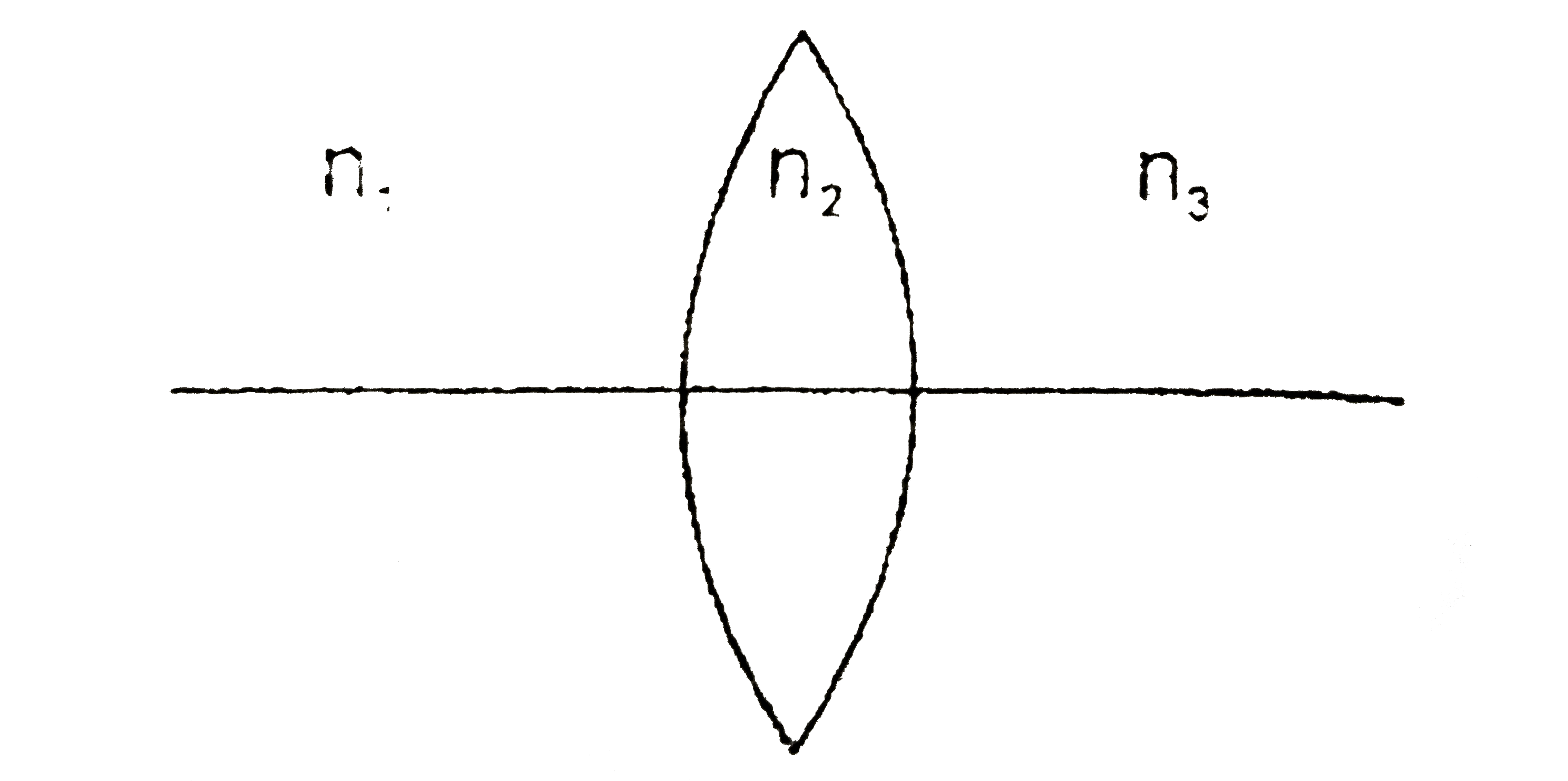
View SolutionA convex lens of refractive index 3/2 has a power of 2.5∘. If it is placed in a liqud of refractive index 2,the new power of the lens is
View SolutionThe refractive index of water is 43 and glass is 32. What is the refractive index of glass with respect to water ?
View SolutionA double convex lens of refractive index m1 is immersed in a liquid of refractive index m2. This lens will act as:
View SolutionA glass lens of refractive index 1.45 when immersed in a transparent liquid becomes invisible. Under what condition does it happen ?
View SolutionA glass slab of thickness 2cm and refractive index 2 is placed in contact with a biconvex lens of focal length 20cm. The refractive index of the material of the lens 1.5 . The far side of the lens is silvered. Where should an object be placed in front of the slab so that it images on to itself?
View SolutionThe refractive index of glass with respect to air is 1.5. What is the value of the refractive index of air with respect to glass?
View SolutionIf a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
View SolutionA mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
View Solution
