A glass prothole is made at the botton of a ahip for observing sea life. The hole diameter D is much larger than the thickness of the glass. Determine the area S of the field of vision at the sea botton for the porthole of the refractive index of water is μw and the sea depth is h.
The correct Answer is:π[h√μ2w−1+D2]2
To solve the problem of determining the area S of the field of vision at the sea bottom for a porthole in a ship, we will follow these steps:
Step 1: Understanding the Geometry
We start by visualizing the situation. We have a circular porthole at the bottom of a ship, with a diameter D. The porthole is submerged in water at a depth h. The refractive index of water is given as μw.
Step 2: Critical Angle Calculation
The critical angle IC can be determined using Snell's law. The critical angle is defined where light traveling from water to air is refracted at 90∘:
sinIC=1μw
From this, we can find IC:
IC=arcsin(1μw)
Step 3: Finding the Tangent of the Critical Angle
Using the relationship between sine and cosine, we can find tanIC:
tanIC=sinICcosIC
Where:
cosIC=√1−sin2IC=√1−(1μw)2=√μ2w−1μw
Thus:
tanIC=1μw√μ2w−1μw=1√μ2w−1
Step 4: Relating Tangent to Geometry
From the geometry, we can relate the tangent of the critical angle to the dimensions of the porthole:
tanIC=xh
Where x is the horizontal distance from the edge of the porthole to the point directly below the porthole at the sea bottom.
Step 5: Solving for x
Equating the two expressions for tanIC:
xh=1√μ2w−1⟹x=h√μ2w−1
Step 6: Calculating the Diameter of the Field of Vision
The total diameter D0 of the field of vision at the sea bottom can be expressed as:
D0=D+2x=D+2(h√μ2w−1)
Step 7: Calculating the Area S
The area S of the field of vision is given by the area of a circle:
S=π(D02)2=π⎛⎜
⎜
⎜
⎜
⎜
⎜⎝D+2(h√μ2w−1)2⎞⎟
⎟
⎟
⎟
⎟
⎟⎠2
This simplifies to:
S=π4(D+2h√μ2w−1)2
Final Result
Thus, the area S of the field of vision at the sea bottom for the porthole is:
S=π4(D+2h√μ2w−1)2
We start by visualizing the situation. We have a circular porthole at the bottom of a ship, with a diameter D. The porthole is submerged in water at a depth h. The refractive index of water is given as μw.
The critical angle IC can be determined using Snell's law. The critical angle is defined where light traveling from water to air is refracted at 90∘:
sinIC=1μw
From this, we can find IC:
IC=arcsin(1μw)
Using the relationship between sine and cosine, we can find tanIC:
tanIC=sinICcosIC
Where:
cosIC=√1−sin2IC=√1−(1μw)2=√μ2w−1μw
Thus:
tanIC=1μw√μ2w−1μw=1√μ2w−1
From the geometry, we can relate the tangent of the critical angle to the dimensions of the porthole:
tanIC=xh
Where x is the horizontal distance from the edge of the porthole to the point directly below the porthole at the sea bottom.
Equating the two expressions for tanIC:
xh=1√μ2w−1⟹x=h√μ2w−1
The total diameter D0 of the field of vision at the sea bottom can be expressed as:
D0=D+2x=D+2(h√μ2w−1)
The area S of the field of vision is given by the area of a circle:
S=π(D02)2=π⎛⎜
⎜
⎜
⎜
⎜
⎜⎝D+2(h√μ2w−1)2⎞⎟
⎟
⎟
⎟
⎟
⎟⎠2
This simplifies to:
S=π4(D+2h√μ2w−1)2
Thus, the area S of the field of vision at the sea bottom for the porthole is:
S=π4(D+2h√μ2w−1)2
Topper's Solved these Questions
Similar Questions
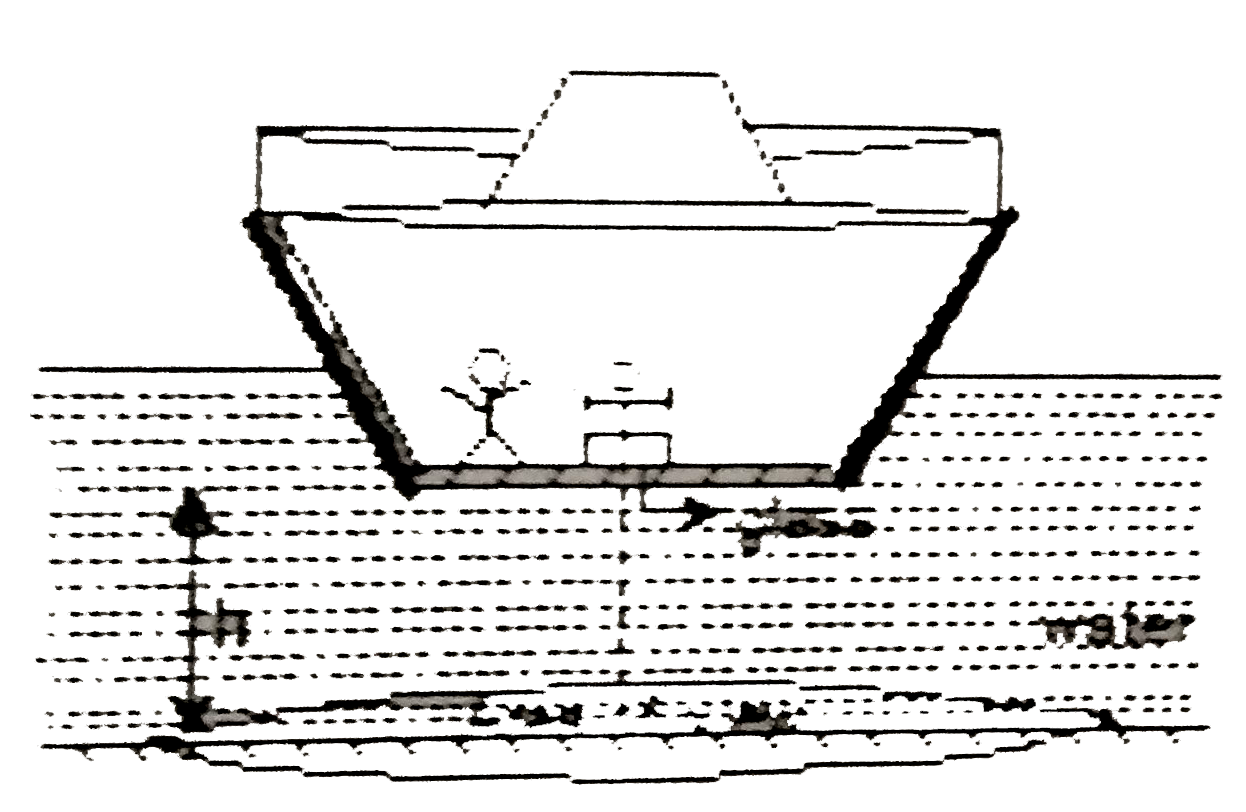
A glass slab of diameter D=20cm is made at the base of a ship as shown in figure. Diameter of glass slab is much larger than the thickness of the glass slab. The area 'S' of the field of view at the sea bottom if μwater=4/3, μglass=3/2 & the depth of sea base beow the slab is h=√7m is
View SolutionA spider and a fly are on the surface of a glass sphere. As the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it? Assume that the radius of the sphere (R) is much larger than the sizes of the spider and the fly. take the refractive index of glass μg to be equal to √2.
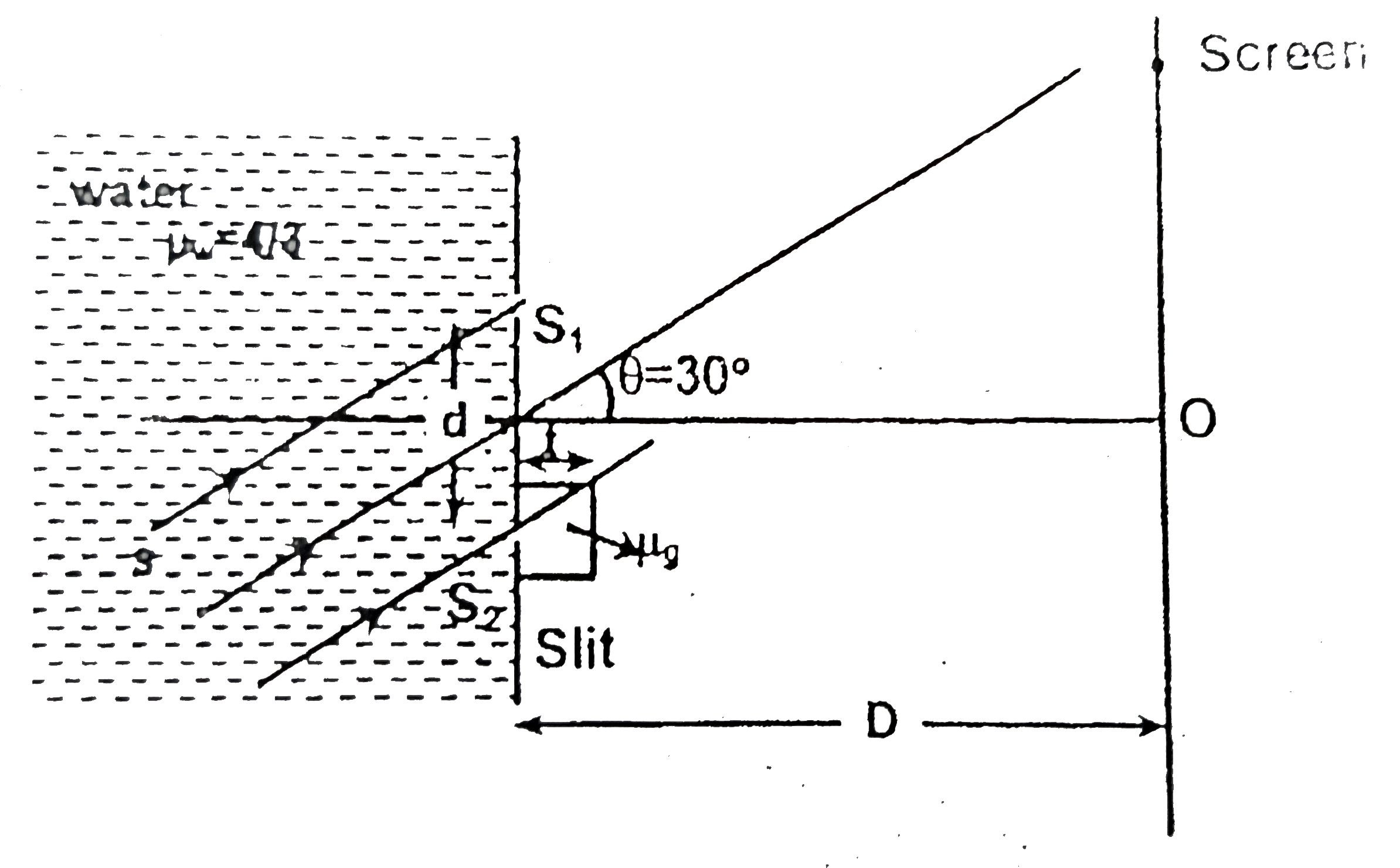
View SolutionIn a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.

(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. What is the viscous force on a glass sphere of radius r=1mm falling through water (η=1×10−3Pa−s) when the sphere has speed of 3m/s?
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. If the sphere in previous question has mass of 1×10−5kg what is its terminal velocity when falling through water? (η=1×10−3Pa−s)
A. 1.3m/s
B. 3.4m/s
C. 5.2m/s
D. 6.5m/s
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−s
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−3m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?
View SolutionA screen is at distance D=80 cm form a diaphragm having two narrow slits S1 and S2 which are d=2 mm apart.
Slit S1 is covered by a transparent sheet of thickness
t1=2.5μm slit S2 is covered by another sheet of thickness
t2=1.25μm as shown if Fig. 2.52.
Both sheets are made of same material having refractive index μ=1.40
Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength λ=5000Å is incident normally on the diaphragm.
Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (μw=4/3)

View Solution
