Two long straight parallel conductors are separated by a distance of 5 cm and carrying current 20 A. what work per unit length of a conductor must be done to increases the separation between conductors to 10 cm, if the current flows in the same direction ?
The correct Answer is:A, B, D
To solve the problem of calculating the work done per unit length to increase the separation between two long straight parallel conductors carrying current in the same direction, we can follow these steps:
1. Identify Given Values:
- Initial separation, d1=5cm=0.05m
- Final separation, d2=10cm=0.10m
- Current in each conductor, I1=I2=20A
2. Formula for Force Between Conductors:
The force per unit length F between two parallel conductors carrying currents in the same direction is given by:
F=μ0I1I22πd
where μ0=4π×10−7T m/A is the permeability of free space, and d is the separation between the conductors.
3. Calculate Initial Force per Unit Length:
Substitute the initial separation d1 into the formula:
F1=(4π×10−7)⋅(20)⋅(20)2π⋅0.05
Simplifying this:
F1=(4×20×20)×10−72×0.05
F1=1600×10−70.1=16000×10−7=1.6×10−3N/m
4. Calculate Final Force per Unit Length:
Now substitute the final separation d2:
F2=(4π×10−7)⋅(20)⋅(20)2π⋅0.10
Simplifying this:
F2=(4×20×20)×10−72×0.10
F2=1600×10−70.2=8000×10−7=0.8×10−3N/m
5. Calculate Work Done:
The work done W to separate the conductors from d1 to d2 can be calculated using the integral of force over distance:
W=∫d2d1Fdx
Since the force varies with distance, we can express it as:
W=∫0.100.05μ0I1I22πxdx
Substituting the values:
W=(4π×10−7)⋅(20)⋅(20)2π∫0.100.051xdx
The integral of 1x is lnx:
W=800×10−71(ln(0.10)−ln(0.05))
W=800×10−7ln(2)(since ln(0.10)−ln(0.05)=ln(2))
6. Final Calculation:
Using ln(2)≈0.693:
W=800×10−7×0.693≈5.544×10−5J/m
Final Answer:
The work done per unit length to increase the separation between the conductors from 5 cm to 10 cm is approximately:
W≈5.544×10−5J/m
- Initial separation, d1=5cm=0.05m
- Final separation, d2=10cm=0.10m
- Current in each conductor, I1=I2=20A
The force per unit length F between two parallel conductors carrying currents in the same direction is given by:
F=μ0I1I22πd
where μ0=4π×10−7T m/A is the permeability of free space, and d is the separation between the conductors.
Substitute the initial separation d1 into the formula:
F1=(4π×10−7)⋅(20)⋅(20)2π⋅0.05
Simplifying this:
F1=(4×20×20)×10−72×0.05
F1=1600×10−70.1=16000×10−7=1.6×10−3N/m
Now substitute the final separation d2:
F2=(4π×10−7)⋅(20)⋅(20)2π⋅0.10
Simplifying this:
F2=(4×20×20)×10−72×0.10
F2=1600×10−70.2=8000×10−7=0.8×10−3N/m
The work done W to separate the conductors from d1 to d2 can be calculated using the integral of force over distance:
W=∫d2d1Fdx
Since the force varies with distance, we can express it as:
W=∫0.100.05μ0I1I22πxdx
Substituting the values:
W=(4π×10−7)⋅(20)⋅(20)2π∫0.100.051xdx
The integral of 1x is lnx:
W=800×10−71(ln(0.10)−ln(0.05))
W=800×10−7ln(2)(since ln(0.10)−ln(0.05)=ln(2))
Using ln(2)≈0.693:
W=800×10−7×0.693≈5.544×10−5J/m
The work done per unit length to increase the separation between the conductors from 5 cm to 10 cm is approximately:
W≈5.544×10−5J/m
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Two long straight parallel conductors separated by a distance of 0.5m carry currents of 5A and 8A in the same direction. The force per unit length experienced by each other is
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View Solution
Knowledge Check
The two linear parallel conductors carrying currents in the opposite direction…………………each other.
AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
Two long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View Solutionin given figure X and Y are two long straight parallel conductor each carrying a current 2 A. the force per unit length on each conductor is F. when the current in each is changed to 1 A and reversed in direction. the force per unit length on each is now

View SolutionShown in Fig. is an end-on view of three long, straight, parallel conductors spaced equal distances a apart. The outer conductors carry current I out of the page, the middle conductor carries current I into the page. Where in the plane of the page is the magnetic field zero?
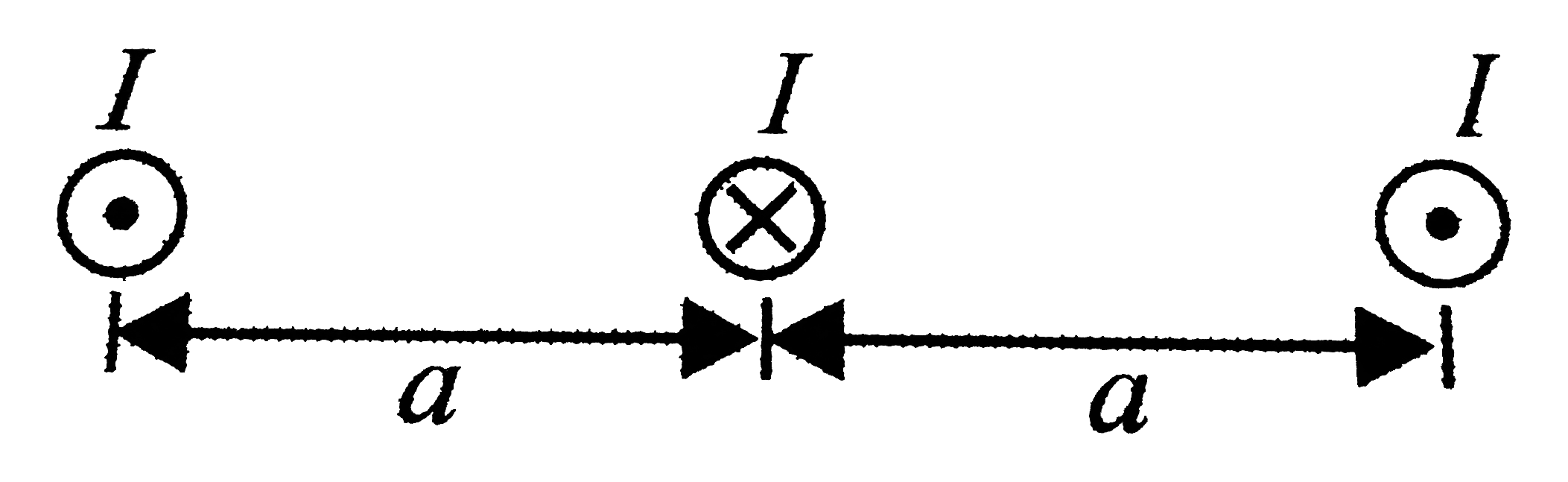
View SolutionTwo parallel wires separated by a distance of 10cm carry currents of 10 A and 40 A along the same direction, Where should a third current be placed so that it experience no magnetic force?
View SolutionAnswer the following:
(a)Define SI unit of current in terms of the force between two parallel current carrying conductors.
(b) Two long straight parallel conductors carrying steady currents IaandIb along the same direction are separated by a distance d. How does one explain the force of attraction between them? If a third conductor carrying a current Ic in the opposite direction is placed just in the middle of these conductors , find the resultant force acting on the third conductor.
View SolutionTwo long parallel straight wires X and Y separated by a distance 5cm in air carry currents of 10A and 5A respectively in opposite directions. Calculate the magnitude and direction of force on a 20cm length of the wire Y. Figure

View Solution
