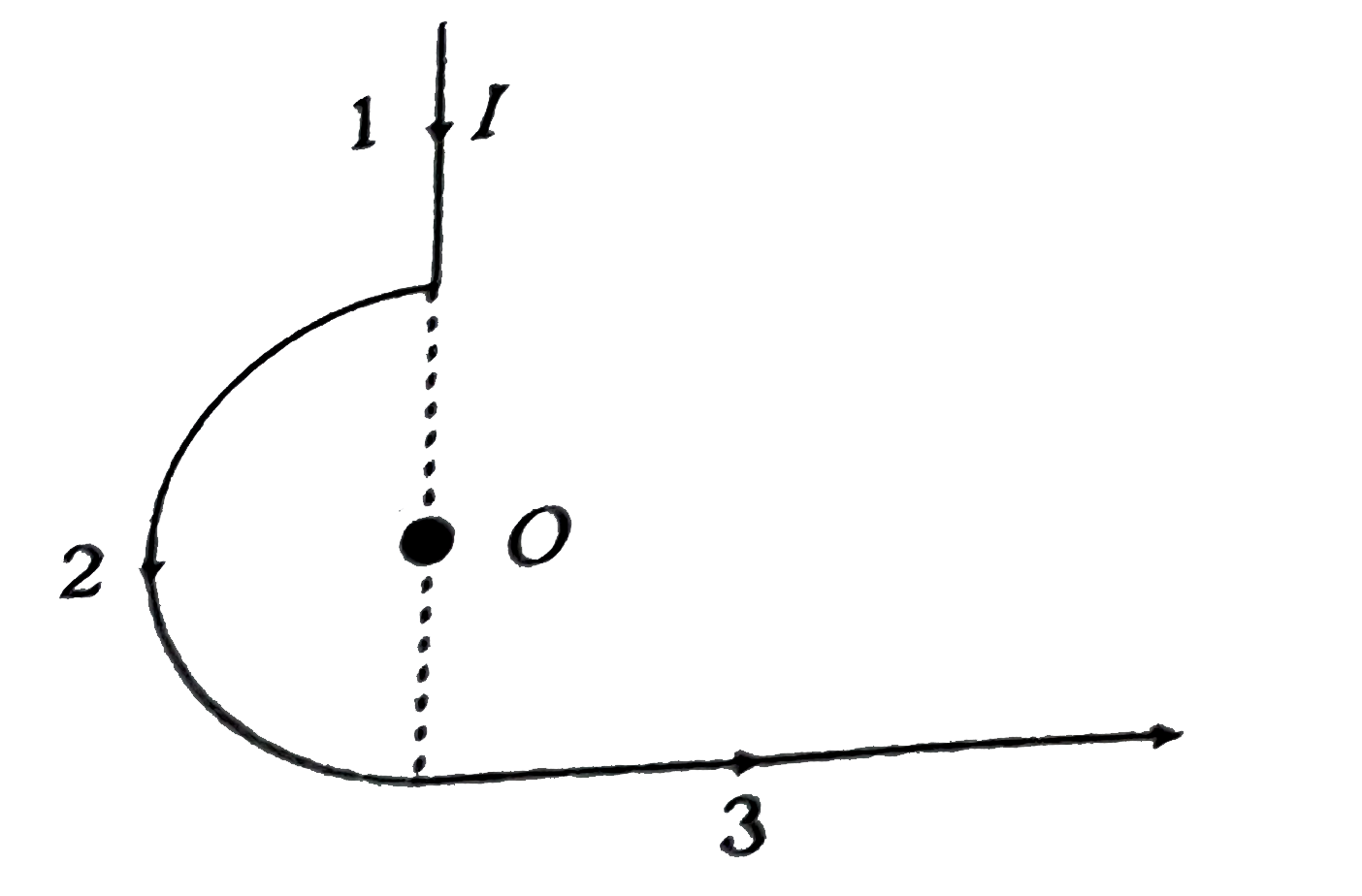
The magnetic field at the origin due to the current flowing in the wire is
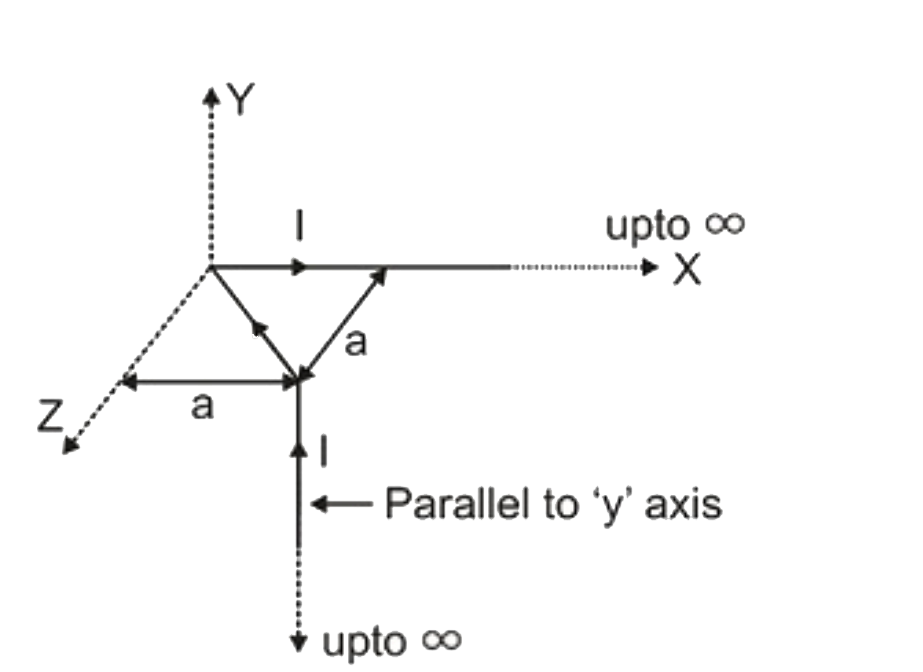
−μ0I8πa(ˆi+ˆk)
μ0I2πa(ˆi+ˆk)
μ0I8πa(−ˆi+ˆk)
μ0I4πa√2(ˆi+ˆk)
The correct Answer is:C
BOD=0
BOB=0
BAB=μ0l4πa√2[cos45∘(−ˆi)−cos45∘ˆk]=μ0I8πa(−ˆi+ˆk)

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-2
26 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3
18 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Find the field at the origin O due to the current i=2A.
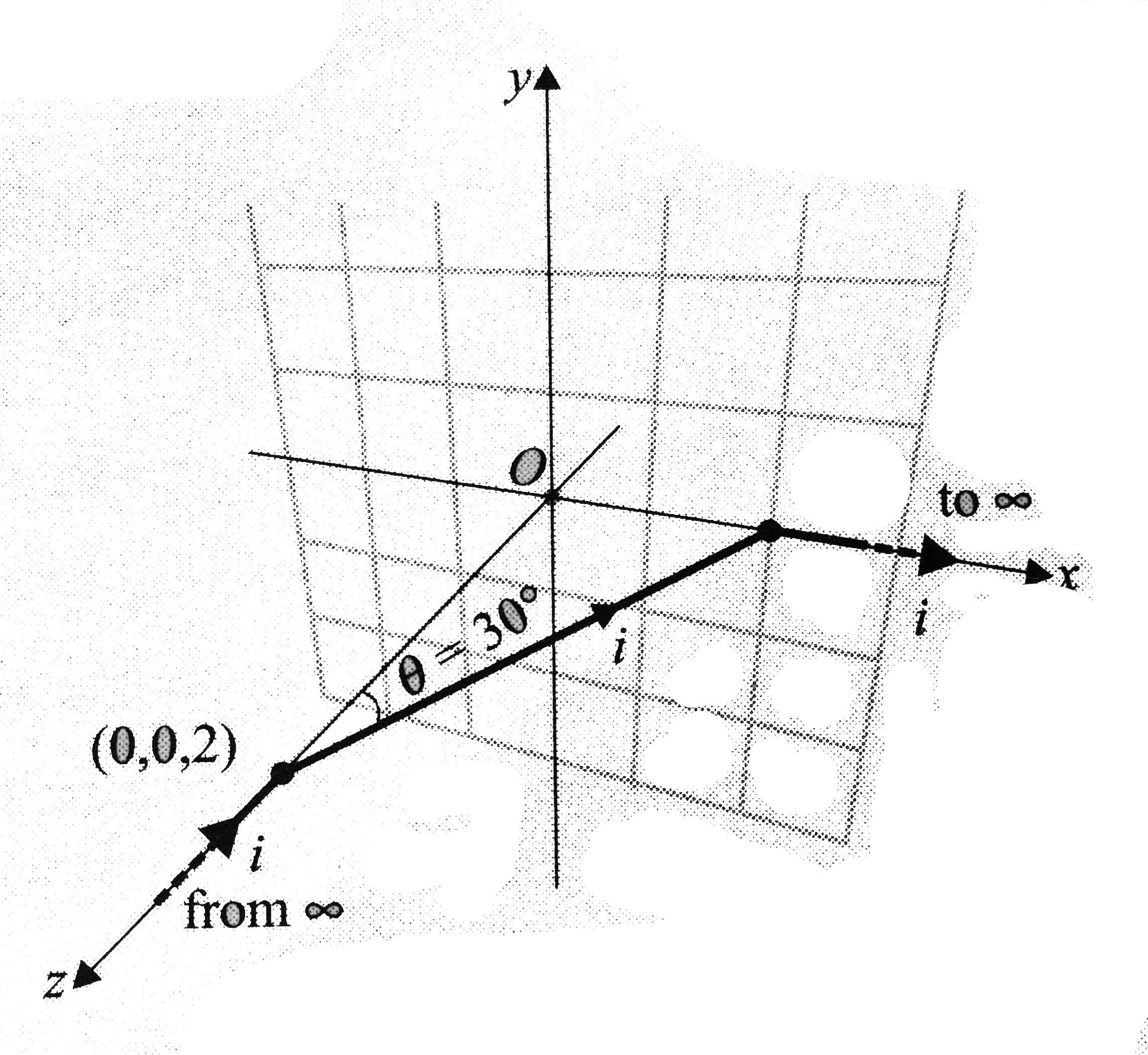
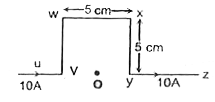
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View SolutionThe magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionWhat will be the resulatant field at the origin due to the four indinite length wires if each wire produces magnetic field B at origin ?
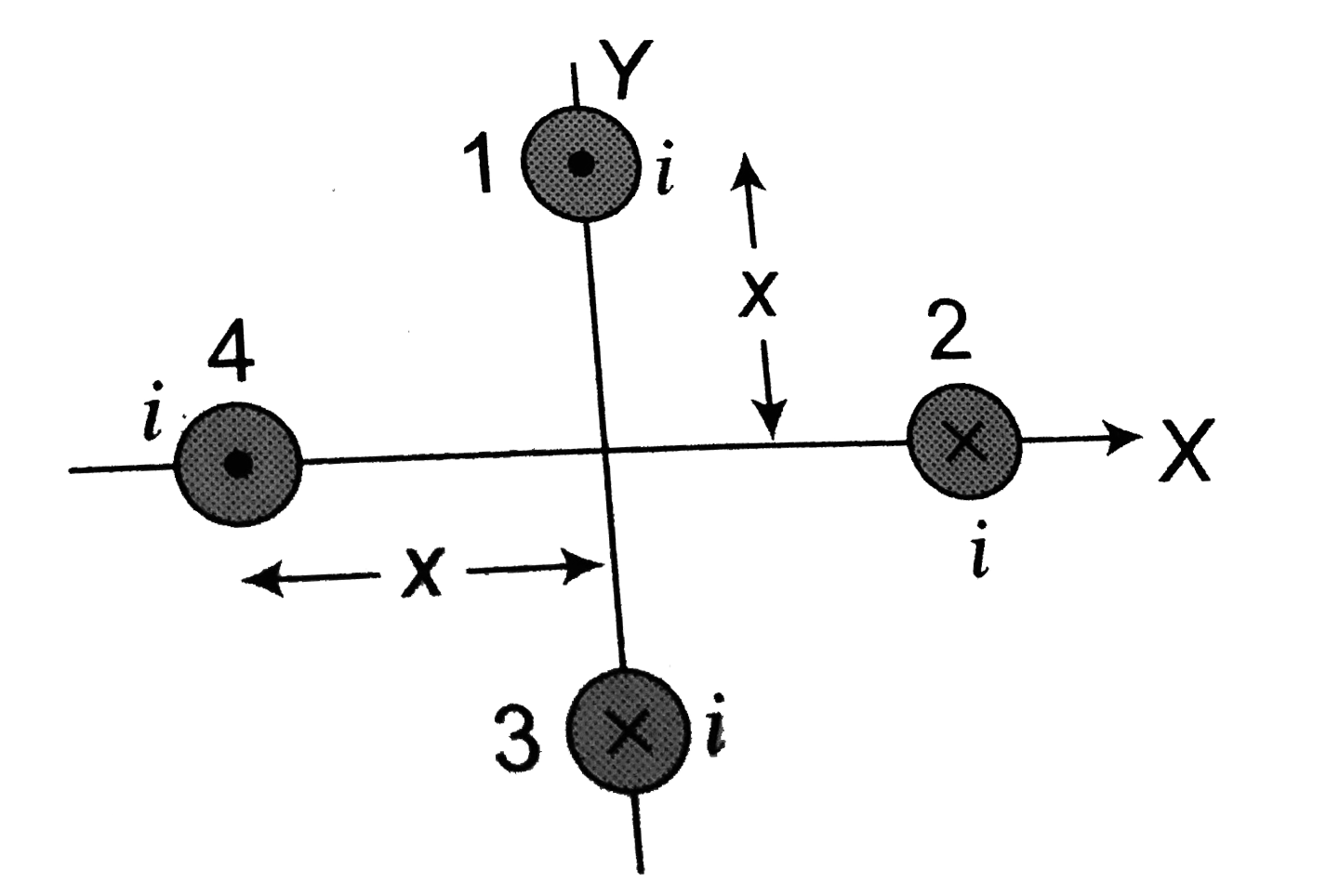
View SolutionWhat will be the resulatant field at the origin due to the four indinite length wires if each wire produces magnetic field B at origin ?

View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
View SolutionThe magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.

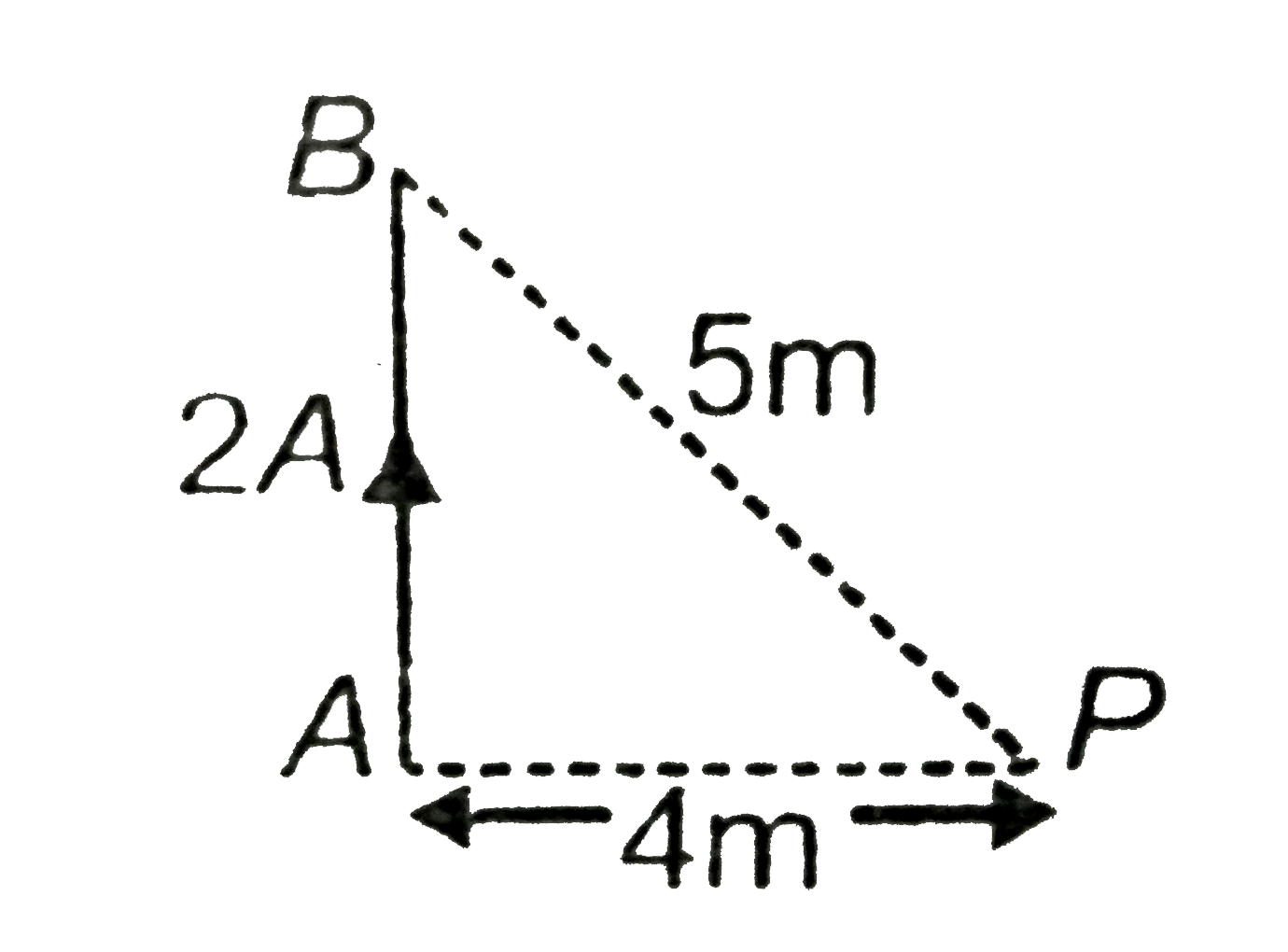
View SolutionWhat is the magnetic field ∣∣→B∣∣ at the point P due to a current carrying wire of length AB (having a current of 2A) shown in figure ?
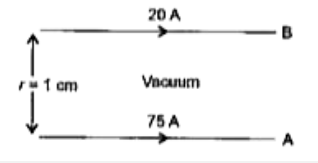
View SolutionCalculate force per unit length acting on the wire B due to the current flowing in the wire A. (see figure below)
View Solution