The magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.

μ0I2πd(cosϕ1+cosϕ2)
μ04π2Id(tanθ1+tanθ2)
μ04πId(sinϕ1+sinϕ2)
μ04πId(cosθ1+cosθ2)
The correct Answer is:A
(a) Using B=μ0i4πa[sinθ1+sinθ2]
But θ1+ϕ1=90∘orθ1=90∘−ϕ,
sinθ1=sin(90∘−ϕ1)=cosϕ1
Similarly, sinθ2=cosϕ2
Bnet=μ0I2πa(cosϕ1+cosϕ2)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
The magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionFind the magnetic field at centre P due to current i in the conductor as shown in fig.

View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
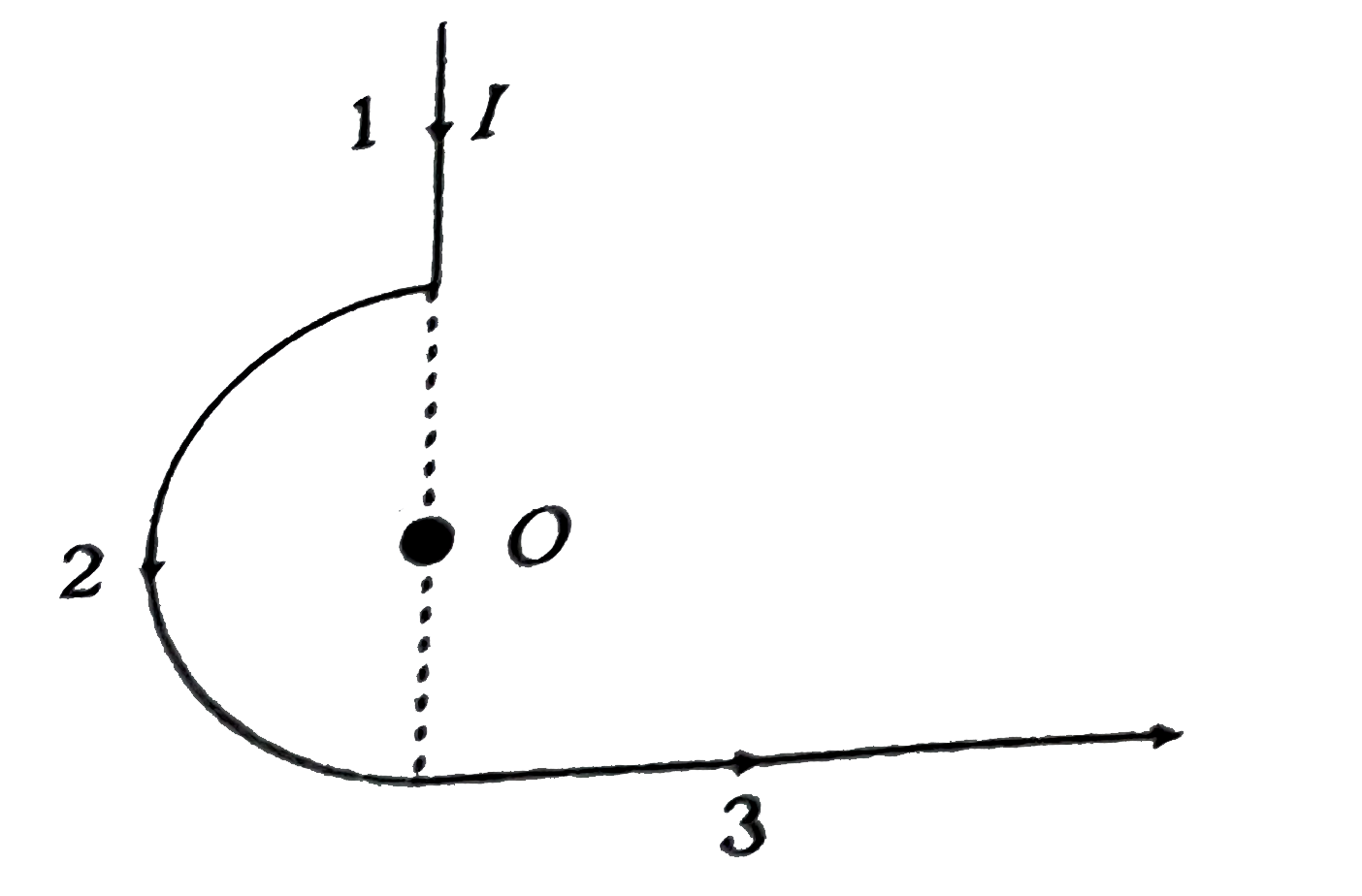
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
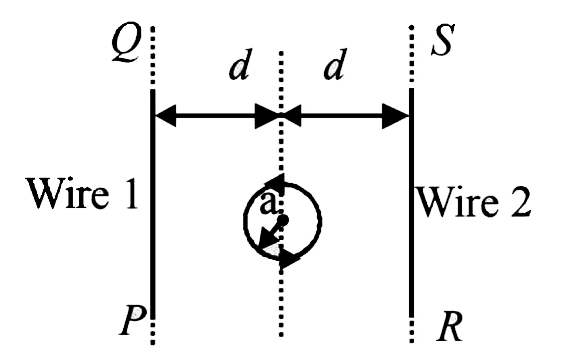
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that case
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
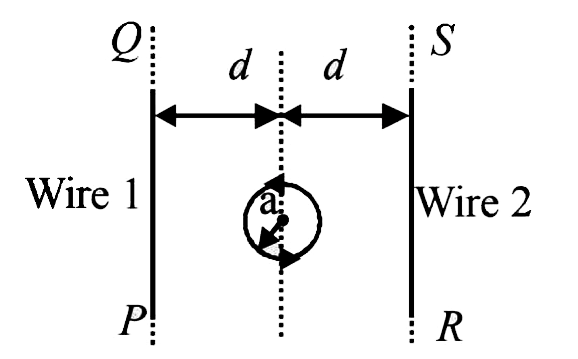
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
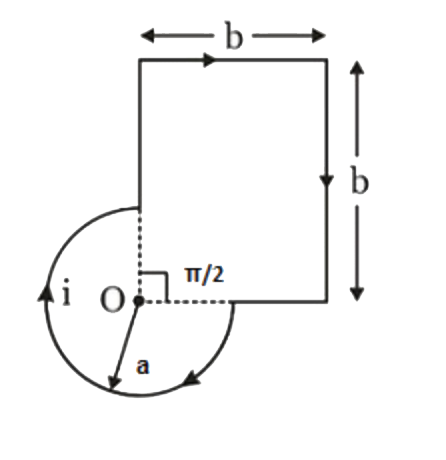
View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
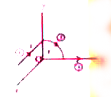
View SolutionFind the magnetic field at the origin in the fig. Shown in fig.

View Solution
