Write the expression for the magnetic moment (m) due to a planar square loop of side 'l' carrying a steady current I in a vector form.
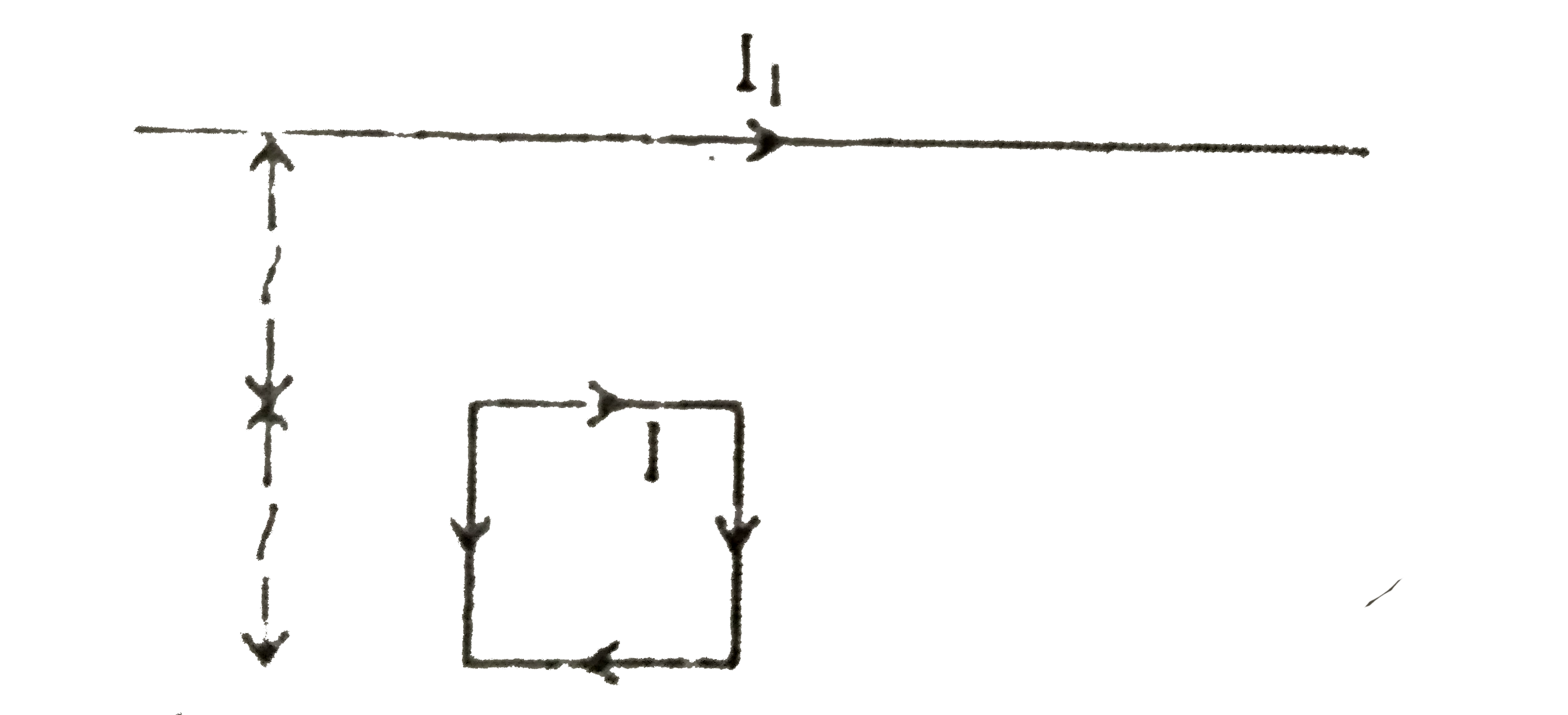
In the given figure, this loop is placed in a horizontal plane near a long straight conductor carraying a steady current at a distance l as shown. Give reason to explain that the loop will exerience a net force but no torque. Write the expression for this force acting on the loop.
The expression for the magnetic moment due to a planar square loop of side carrying a steady current in a vector form is given as
Therefore,
Where, is the unit vector along the normal to the surface of the loop. The attractive force on the loop is
The repulsive force on the loop is
=
Since the attractive force is greater than the repulsive forrce, a net force acts on the loop. The torque on the loop is given as
( Area vector is parallel to the magnetic field)
The torque acting on the loop is zero.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-2
27 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
(i) Write the expression for the magnetic moment (→m) due to a planar square loop of side 'l' carrying a steady current I in a vector form.
(ii) In figure., this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the donductor as shown in figure. The loop will experience
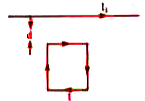
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long staright conductor carryinf a steady current I, at a distance d from the conductor as shown in Fig. The loop wil experience

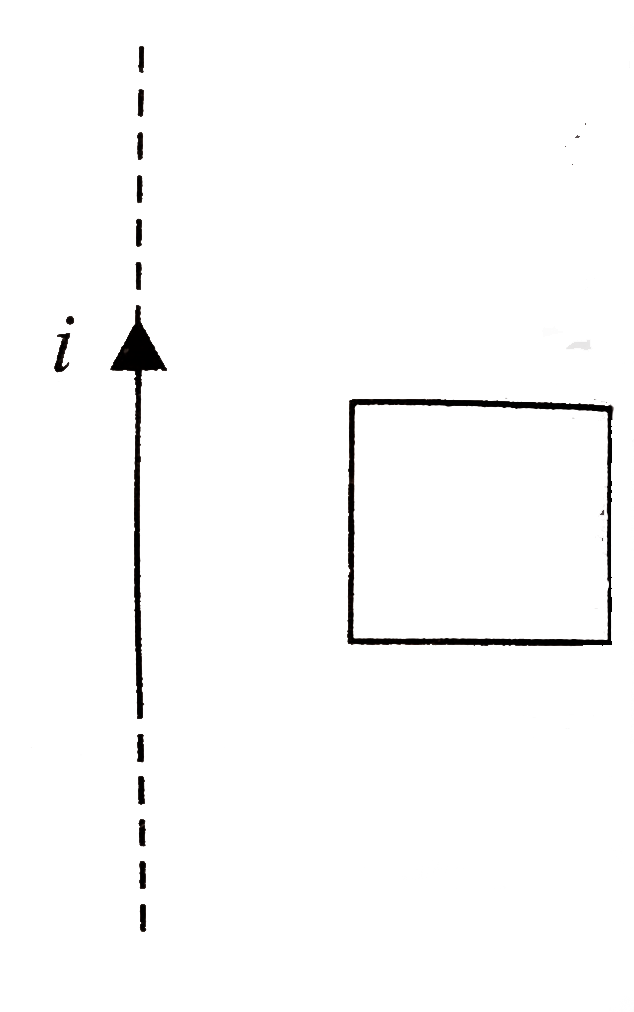
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.

View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
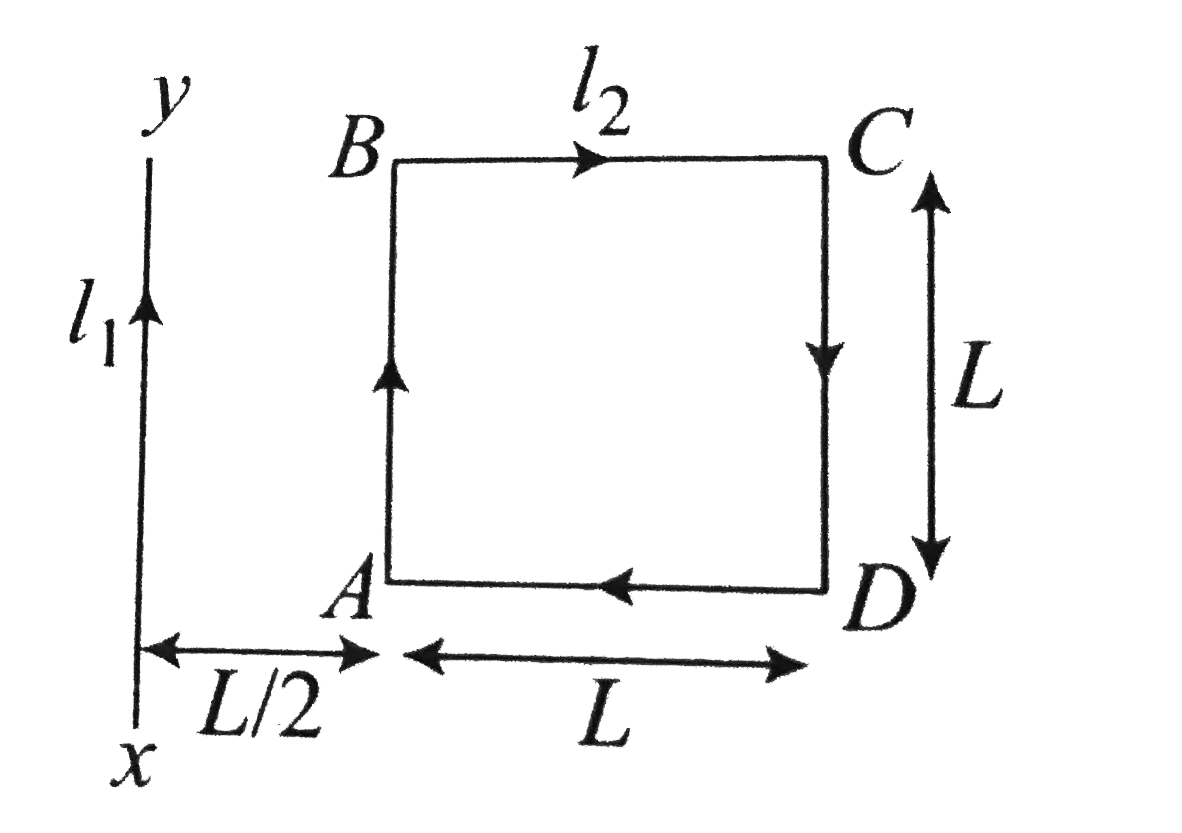
View SolutionA square loop ABCD, carrying a current I2 is placed near and coplanar with a long straight conductor XY, carrying a current I1 as shwon in Figure. The net force on the loop will be
View SolutionA conductor AB of length l carrying current i is placed perpendicular to a long straight conductor carrying a current I as shown. Force on AB will be

View SolutionThe magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View Solution
