A non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in the region of space between y=0 and y=d. A particle of mass m and positive charge q has velocity →v=3qB0dmˆi at origin O. Find the angle made by velocity of the particle withe the positive x-axis when it leaves the field. (Ignore any interaction other than magnetic field)
90∘
30∘
60∘
45∘
The correct Answer is:C
To solve the problem, we need to analyze the motion of a charged particle in a non-uniform magnetic field. The magnetic field is given by →B=B0(1+yd)(−^k) and the particle has an initial velocity →v=3qB0dm^i at the origin. We will find the angle made by the velocity of the particle with the positive x-axis when it leaves the field.
1. Identify the Forces Acting on the Particle:
The magnetic force acting on a charged particle moving in a magnetic field is given by:
→F=q→v×→B
Here, →v=3qB0dm^i and →B=B0(1+yd)(−^k).
2. Calculate the Cross Product:
We need to calculate →v×→B:
→F=q(3qB0dm^i)×(B0(1+yd)(−^k))
Using the right-hand rule for the cross product:
^i×(−^k)=^j
Therefore, the force becomes:
→F=−qB0(1+yd)3qB0dm^j
Simplifying this gives:
→F=−3q2B20dm(1+yd)^j
3. Determine the Acceleration:
The acceleration →a can be found using Newton's second law:
→F=m→a⟹→a=→Fm=−3q2B20dm2(1+yd)^j
4. Find the Change in Velocity:
The velocity in the y-direction changes due to the acceleration. The time spent in the magnetic field can be determined by the distance traveled in the y-direction, which is d. The time t can be calculated using:
t=dvx=d3qB0dm=m3qB0
5. Calculate the Change in Velocity in the y-direction:
The change in velocity in the y-direction is given by:
Δvy=ay⋅t=−3q2B20dm2(1+dd)⋅m3qB0
Simplifying this gives:
Δvy=−3q2B20dm2⋅m3qB0⋅2=−2qB0dm
6. Final Velocity Components:
The final velocity in the y-direction is:
vy=0+Δvy=−2qB0dm
The final velocity in the x-direction remains unchanged:
vx=3qB0dm
7. Calculate the Angle:
The angle θ with respect to the x-axis is given by:
tan(θ)=vyvx=−2qB0dm3qB0dm=−23
Therefore, the angle θ is:
θ=tan−1(−23)
Final Result:
The angle made by the velocity of the particle with the positive x-axis when it leaves the field is:
θ≈−33.69∘
This indicates that the particle is moving downwards relative to the positive x-axis.
The magnetic force acting on a charged particle moving in a magnetic field is given by:
→F=q→v×→B
Here, →v=3qB0dm^i and →B=B0(1+yd)(−^k).
We need to calculate →v×→B:
→F=q(3qB0dm^i)×(B0(1+yd)(−^k))
Using the right-hand rule for the cross product:
^i×(−^k)=^j
Therefore, the force becomes:
→F=−qB0(1+yd)3qB0dm^j
Simplifying this gives:
→F=−3q2B20dm(1+yd)^j
The acceleration →a can be found using Newton's second law:
→F=m→a⟹→a=→Fm=−3q2B20dm2(1+yd)^j
The velocity in the y-direction changes due to the acceleration. The time spent in the magnetic field can be determined by the distance traveled in the y-direction, which is d. The time t can be calculated using:
t=dvx=d3qB0dm=m3qB0
The change in velocity in the y-direction is given by:
Δvy=ay⋅t=−3q2B20dm2(1+dd)⋅m3qB0
Simplifying this gives:
Δvy=−3q2B20dm2⋅m3qB0⋅2=−2qB0dm
The final velocity in the y-direction is:
vy=0+Δvy=−2qB0dm
The final velocity in the x-direction remains unchanged:
vx=3qB0dm
The angle θ with respect to the x-axis is given by:
tan(θ)=vyvx=−2qB0dm3qB0dm=−23
Therefore, the angle θ is:
θ=tan−1(−23)
The angle made by the velocity of the particle with the positive x-axis when it leaves the field is:
θ≈−33.69∘
This indicates that the particle is moving downwards relative to the positive x-axis.
Similar Questions
A non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in region of space in between y=0&y=d.The lines are shown in the diagram.A particle of mass m and positive charge q is moving.Given an initial velocity →v=v0ˆi.Find the components of velocity of the particle when it leaves the field.
 View Solution
View SolutionMagnetic field exist in the space and given as →B=−B0l2x2ˆk, where B0and l positive constants. A particle having positive charge 'q' and mass 'm' is pojected wit speed 'v0' along positive x axis from the origin. What is the maimum distance of the charged particle from the y-axis before it turns back due to the magnetic field. (Ignore any interaction other than magnetic field)
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is
 View Solution
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then
 View Solution
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then
 View Solution
View SolutionThe space has electromagnetic field which is given as →B=−B0ˆk and →E=E0ˆk. A charged particle having mass m and positive charge q is given velocity v0ˆi at origin at t=0sec. The z coordinate of the particle when it passes through the z−axis is (neglect gravity through motion)
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is
2mvqB
 View Solution
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.View SolutionThe region between y =0 and y=d constains a magnetic field →B=B→z. A particle of mass m and charge q enters of the region with a velocity →v=v→i. If d=mv2qB the acceleration of the charged particle at the point of its emergence at the other side is :
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
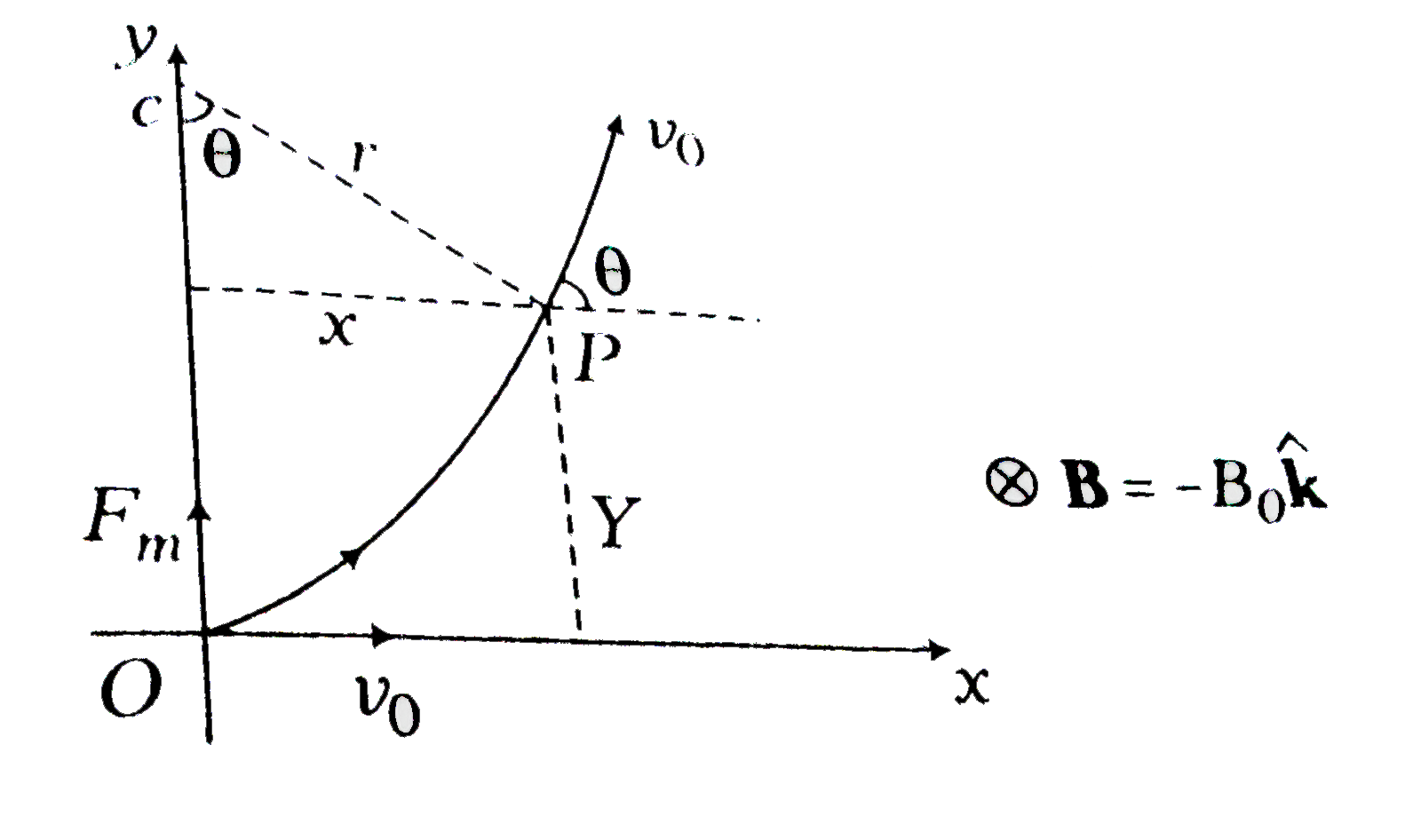
View Solution

