Two coils of self inductance 100 mH and 400 mH are placed very closed to each other. Find maximum mutual inductance between the two when 4 A current passes through them.
200mH
300mH
100√2mH
None of these
The correct Answer is:A
To solve the problem of finding the maximum mutual inductance between two coils with given self-inductances, we will follow these steps:
1. Identify the Given Values:
- Self-inductance of the first coil, L1=100mH=100×10−3H
- Self-inductance of the second coil, L2=400mH=400×10−3H
2. Understand the Formula for Maximum Mutual Inductance:
- The formula for maximum mutual inductance M between two coils is given by:
Mmax=√L1×L2
3. Substitute the Values into the Formula:
- Substitute L1 and L2 into the formula:
Mmax=√(100×10−3)×(400×10−3)
4. Calculate the Product:
- First, calculate the product:
100×400=40000
- Then, include the powers of ten:
40000×10−6=40×10−3=0.04
5. Take the Square Root:
- Now, take the square root:
Mmax=√0.04=0.2H=200mH
6. Final Answer:
- Therefore, the maximum mutual inductance Mmax between the two coils is:
200mH
- Self-inductance of the first coil, L1=100mH=100×10−3H
- Self-inductance of the second coil, L2=400mH=400×10−3H
- The formula for maximum mutual inductance M between two coils is given by:
Mmax=√L1×L2
- Substitute L1 and L2 into the formula:
Mmax=√(100×10−3)×(400×10−3)
- First, calculate the product:
100×400=40000
- Then, include the powers of ten:
40000×10−6=40×10−3=0.04
- Now, take the square root:
Mmax=√0.04=0.2H=200mH
- Therefore, the maximum mutual inductance Mmax between the two coils is:
200mH
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
Knowledge Check
Two coil are placed close to each other. The mutual inductance of the pair of coils depends upon.
Amedium between the coilsBdistance between the two coilsCorientation of the two coilsDall of theseTwo coils of self-inductance 2mH and 8mH are placed so close together that the effective flux in one coil is completely linked with the other. The mutual inductance between these coil is
A16 mHB10 mHC6 mHD4 mH
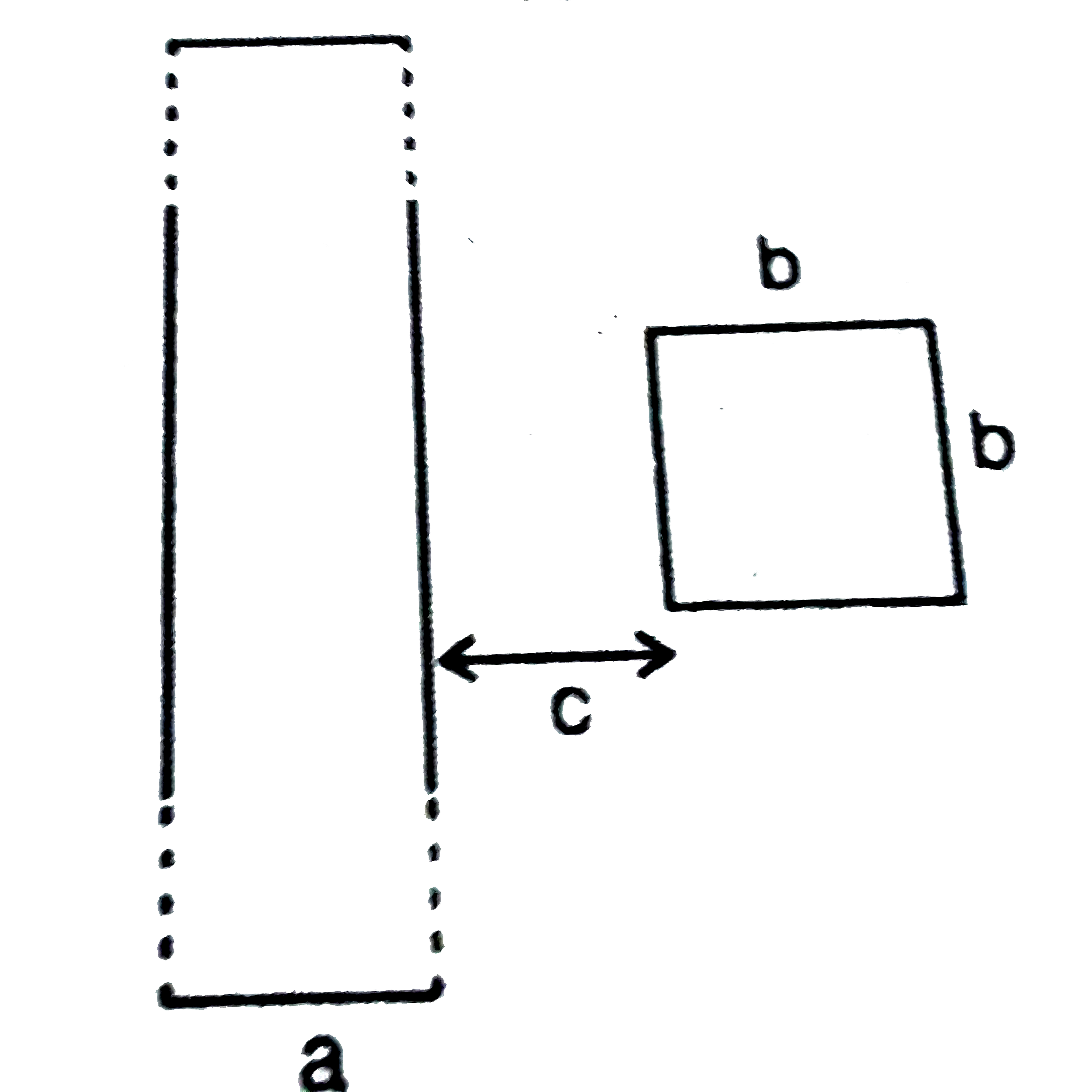
Find the mutual inductance between two rectangular loops, shown in the figure.
View SolutionTwo coils of self-inductance L1 and L2 are placed closed to each other so that total flux in one coil is completely linked with other. If M is mutual inductance between them, then
View SolutionTwo different coils of self inductance L 1 and L 2 are placed close to each other so that the effective flux in one coil is completely linked with other. If M is the mutual inductance between them, then

View SolutionName two factors on which mutual inductance between a pair of coils depends?
View SolutionThe self-inductances of two identical coils are 0.1H. They are wound over each other. Mutual inductance will be-
View SolutionTwo coils of self-inductance 2mH and 8mH are placed so close together that the effective flux in one coil is completely linked with the other. The mutual inductance between these coil is
View Solution
