A rectangular loop of sides 'a' and 'b' is placed in xy plane. A very long wire is also placed in xy plane such that side of length 'a' of the loop is parallel to the wire. The distance between the wire and the nearest edge of the loop is 'd'. The mutual inductance of this system is proportional to :
a
b
1d
current in wire
The correct Answer is:A
To solve the problem of finding the mutual inductance of a rectangular loop placed parallel to a long wire, we can follow these steps:
Step 1: Understand the Configuration
We have a rectangular loop with sides 'a' and 'b' placed in the xy-plane. A long wire is also in the xy-plane, parallel to the side of length 'a' of the loop. The distance between the wire and the nearest edge of the loop is 'd'.
Hint: Visualize the setup to understand the relationship between the loop and the wire.
Step 2: Define the Current in the Wire
Let the current flowing through the long wire be denoted as I0.
Hint: Identify the current as a variable that will affect the magnetic field.
Step 3: Calculate the Magnetic Field
The magnetic field B at a distance x from the long wire can be expressed using Ampère's law:
B=μ0I02πx
where μ0 is the permeability of free space.
Hint: Remember that the magnetic field around a long straight conductor decreases with distance.
Step 4: Consider a Small Element of the Loop
Take a small element of the loop, dA, at a distance x from the wire. The area of this small element can be expressed as:
dA=adx
where dx is an infinitesimal width of the loop.
Hint: Break down the loop into small segments to simplify the integration process.
Step 5: Calculate the Magnetic Flux
The magnetic flux dΦ through the small area dA is given by:
dΦ=B⋅dA=(μ0I02πx)⋅(adx)
Thus, the total flux Φ through the loop can be found by integrating dΦ from d to b+d:
Φ=∫b+ddμ0I0a2πxdx
Hint: Set up the integral correctly to find the total magnetic flux through the loop.
Step 6: Evaluate the Integral
The integral can be evaluated as follows:
Φ=μ0I0a2π(ln(x))b+dd=μ0I0a2π(ln(b+d)−ln(d))=μ0I0a2πln(b+dd)
Hint: Use properties of logarithms to simplify the expression.
Step 7: Relate Flux to Mutual Inductance
The mutual inductance M is defined by the relation:
Φ=MI0
Thus, we can express M as:
M=ΦI0=μ0a2πln(b+dd)
Hint: Recognize that mutual inductance is proportional to the area of the loop.
Step 8: Identify Proportionality
From the expression for mutual inductance M, we can see that it is directly proportional to the side 'a' of the rectangle:
M∝a
Hint: Focus on the terms in the final expression to determine which variable affects mutual inductance.
Conclusion
The mutual inductance of the system is proportional to the length 'a' of the rectangular loop.
Final Answer: Mutual inductance M is proportional to a.
We have a rectangular loop with sides 'a' and 'b' placed in the xy-plane. A long wire is also in the xy-plane, parallel to the side of length 'a' of the loop. The distance between the wire and the nearest edge of the loop is 'd'.
Let the current flowing through the long wire be denoted as I0.
The magnetic field B at a distance x from the long wire can be expressed using Ampère's law:
B=μ0I02πx
where μ0 is the permeability of free space.
Take a small element of the loop, dA, at a distance x from the wire. The area of this small element can be expressed as:
dA=adx
where dx is an infinitesimal width of the loop.
The magnetic flux dΦ through the small area dA is given by:
dΦ=B⋅dA=(μ0I02πx)⋅(adx)
Thus, the total flux Φ through the loop can be found by integrating dΦ from d to b+d:
Φ=∫b+ddμ0I0a2πxdx
The integral can be evaluated as follows:
Φ=μ0I0a2π(ln(x))b+dd=μ0I0a2π(ln(b+d)−ln(d))=μ0I0a2πln(b+dd)
The mutual inductance M is defined by the relation:
Φ=MI0
Thus, we can express M as:
M=ΦI0=μ0a2πln(b+dd)
From the expression for mutual inductance M, we can see that it is directly proportional to the side 'a' of the rectangle:
M∝a
The mutual inductance of the system is proportional to the length 'a' of the rectangular loop.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution
Knowledge Check
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
A2√2μ0πl2LB8√2μ0πl2LC2√2μ02πl2LD2√2μ0L2πl
A triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA square conducting loop of side L is situated in gravity free space. A small conducting circular loop of redius r(r<<L) is placed at the center of the square loop, with its plane perpendicular to the plane of the square loop. The mutual inductance of the two coils is
View SolutionA square conducting loop of side L is situated in gravity free space. A small conducting circular loop of radius r(r<<L) is placed at the center of the square loop, with its plane perpendicular to the plane of the square loop. The mutual inductance of the two coils is
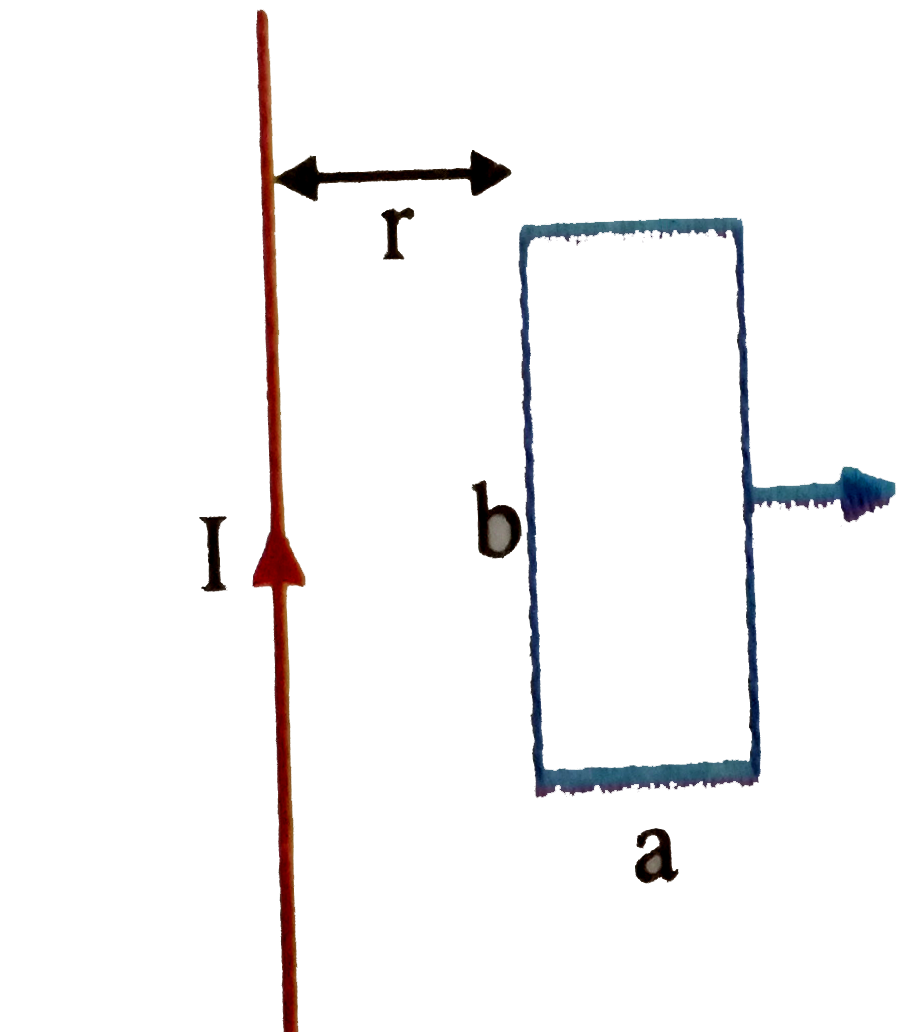
View SolutionA rectangular loop of wire with dimensions shown in figure is coplanar with a long wire carrying current 'I'. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
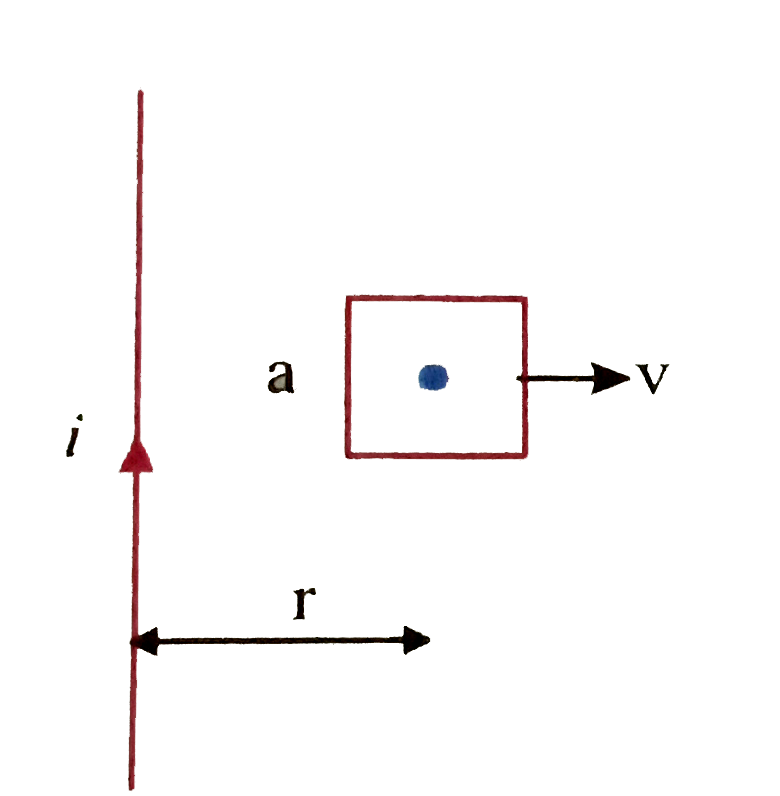
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View SolutionA square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.

View SolutionA square loop of side a is placed at a distance a length away from a long wire carrying a current I1 . If the loop carries a current I2 as shown in the figure . Then the nature of the nature of the force and its amount is

View Solution
