When the current in a certain inductor coil is 5.0A and is increasing at the rate of 10.0A/s,the magnitude of potential difference across the coil is 140V.When the current is 5.0A and decreasing at the rate of 10.0A/s,the potential difference is 60V.The self inductance of the coil is :
2H
4H
10H
12H
The correct Answer is:B
To solve the problem, we will analyze the two cases provided and apply the formula for the potential difference across an inductor.
1. Understanding the Problem:
We have an inductor coil with a current of 5.0 A. The current is increasing at a rate of 10.0 A/s in the first case, resulting in a potential difference of 140 V. In the second case, the current is decreasing at the same rate of 10.0 A/s, leading to a potential difference of 60 V. We need to find the self-inductance L of the coil.
2. Using the Formula for Inductance:
The potential difference e across an inductor can be expressed as:
e=R⋅I+L⋅dIdt
where R is the resistance, I is the current, and dIdt is the rate of change of current.
3. Case 1 (Current Increasing):
- Given:
- I=5.0A
- dIdt=10.0A/s
- e=140V
- Substituting into the formula:
140=R⋅5+L⋅10(Equation 1)
4. Case 2 (Current Decreasing):
- Given:
- I=5.0A
- dIdt=−10.0A/s
- e=60V
- Substituting into the formula:
60=R⋅5−L⋅10(Equation 2)
5. Solving the Equations:
- From Equation 1:
140=5R+10L(1)
- From Equation 2:
60=5R−10L(2)
- Now, we can add both equations to eliminate L:
(140+60)=(5R+10L)+(5R−10L)
200=10R
R=20Ω
6. Substituting R Back to Find L:
- Substitute R=20Ω into Equation 1:
140=5⋅20+10L
140=100+10L
10L=140−100
10L=40
L=4H
Final Answer:
The self-inductance of the coil is L=4H.
We have an inductor coil with a current of 5.0 A. The current is increasing at a rate of 10.0 A/s in the first case, resulting in a potential difference of 140 V. In the second case, the current is decreasing at the same rate of 10.0 A/s, leading to a potential difference of 60 V. We need to find the self-inductance L of the coil.
The potential difference e across an inductor can be expressed as:
e=R⋅I+L⋅dIdt
where R is the resistance, I is the current, and dIdt is the rate of change of current.
- Given:
- I=5.0A
- dIdt=10.0A/s
- e=140V
- Substituting into the formula:
140=R⋅5+L⋅10(Equation 1)
- Given:
- I=5.0A
- dIdt=−10.0A/s
- e=60V
- Substituting into the formula:
60=R⋅5−L⋅10(Equation 2)
- From Equation 1:
140=5R+10L(1)
- From Equation 2:
60=5R−10L(2)
- Now, we can add both equations to eliminate L:
(140+60)=(5R+10L)+(5R−10L)
200=10R
R=20Ω
- Substitute R=20Ω into Equation 1:
140=5⋅20+10L
140=100+10L
10L=140−100
10L=40
L=4H
The self-inductance of the coil is L=4H.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
When the current in the portion of the circuit shown in the figure is 2A and increasing at the rate of 1A/s,the measured potential difference Va−Vb=8V.However when the current is 2A and decreasing at the rate of 1A/s, the measured potential difference Va−Vb=4V.The values of R and L are:
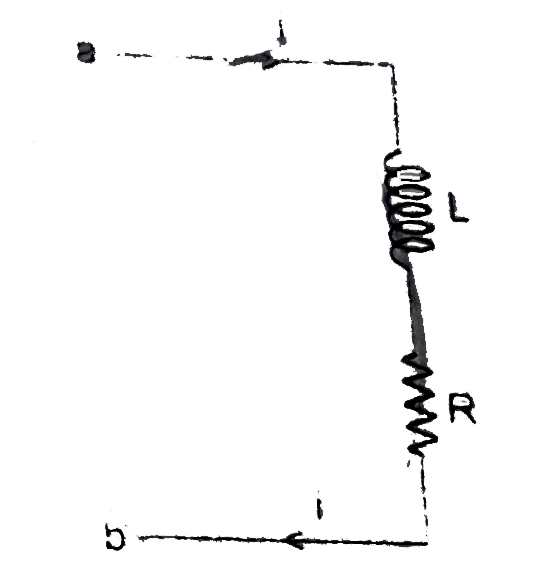
View SolutionIn the circuit (Fig.) what is potential difference VB−VA (in V) when current I is 5A and is decreasing at the rate of 103As−1
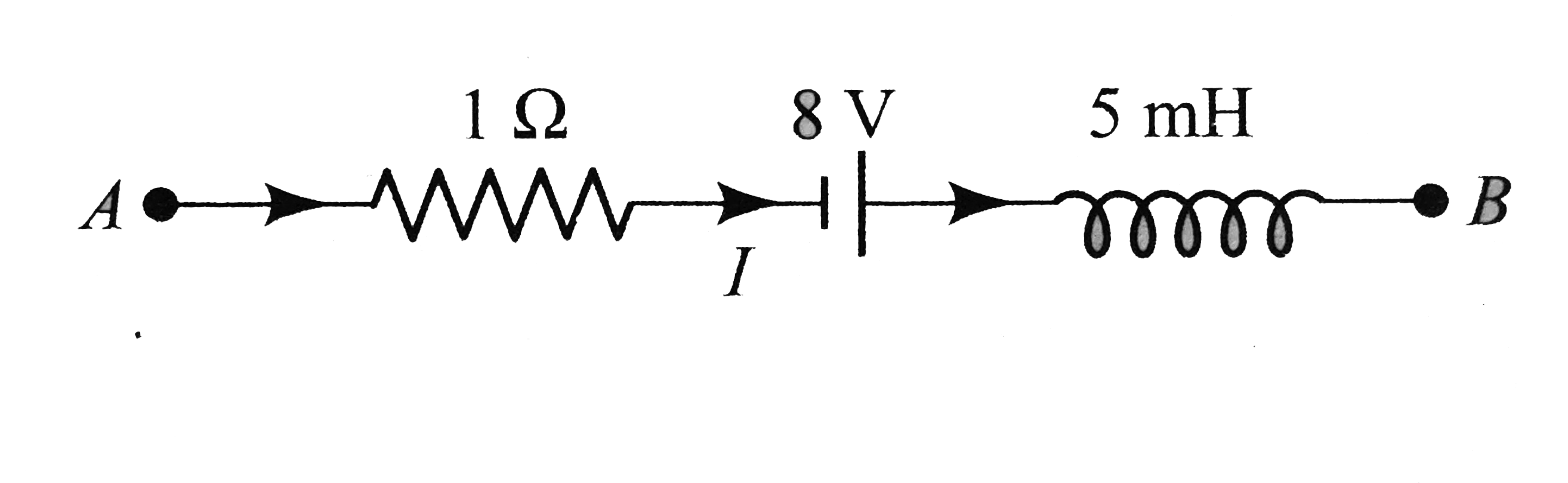
View SolutionIf the instantaneous change on the capacitor is 100μC and current through the circuit is decreasing at the rate of 2×103 As then potential difference VA−VB is equal to
_PHY_E06_046_Q01.png)
View SolutionThe network shown in the figure is a part of complete circuit. What is the potential difference VB−VA when the current I is 5A and is decreasing at a rate of 103A/s?
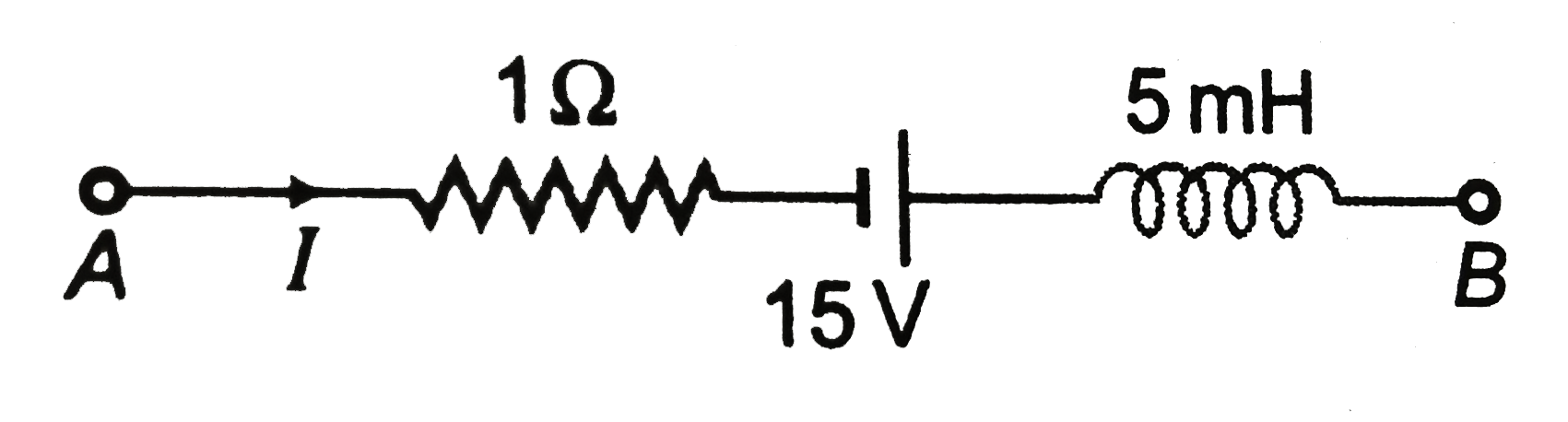
View SolutionThe figure shows an inductor of 2H through which a current increasing at the rate of 5A/sec is flowing.Find the potential difference VX−VY.

View SolutionAn average induced emf of 0.20 V appears in a coil when the current in it is changed from 5.0 A in one direction to 5.0 A in the opposite direction in 0.20 s. find the self inductance of the coil.
View SolutionWhen current in a coil changes from 25 A to 12 A in 0.1 s , average voltage of 50 V is produced .The self inductance of the coil is
View SolutionAn e.m.f. of 12volts is induced in a given coil when the current in it changes at the rate of 48 amperes per minute. The self-inductance of the coil is
View SolutionWhen current in a coil changes from 5 A to 2 A in 0.1 s, average voltage of 50 V is produced. The self - inductance of the coil is :
View SolutionAn emf 96.0mV is induced in the windings of a coil when the current in a nearby coil is increasing at the rate of 1.20A/s. The mutual inductance of the two coils is
View Solution
