A triangular loop as shown in the figure is started to being pulled out at t=0 form a uniform magnetic field with a constant velocity v. Total resistancee of the loop is constant and equal to R. Then the variation of power produced in the loop with time will be :

linearly increasing with time till whole loop come out
increases parabolically till whole loop comes out
Pαt3 till whole loop come out
will be constant with time
The correct Answer is:B
Step by step video & image solution for A triangular loop as shown in the figure is started to being pulled out at t=0 form a uniform magnetic field with a constant velocity v. Total resistancee of the loop is constant and equal to R. Then the variation of power produced in the loop with time will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
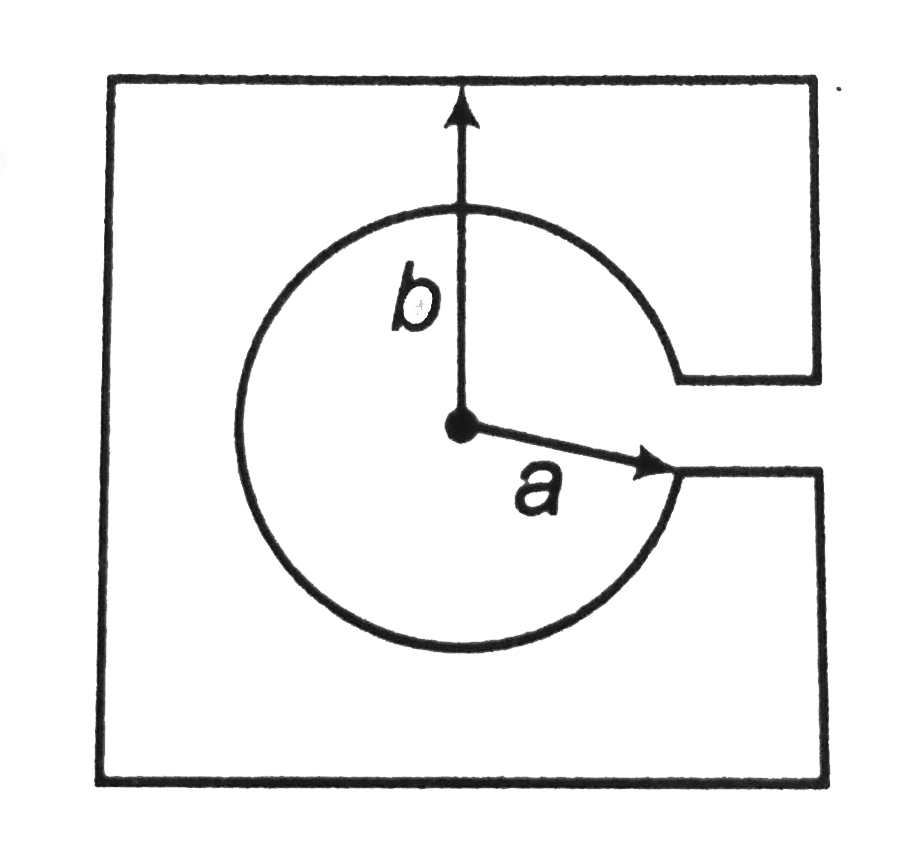
View SolutionA loop shown in the figure is immersed in the varying magnetic field B=B0t, directed into the page. If the total resistance of the loop is R, then the direction and magnitude of induced current in the inner circle is
View SolutionAn equilateral triangular loop ADC having some resistance is pulled with a constant velocity v out of a uniform magnetic field directed in to the paper. At time t=0, side DC of the loop at is at edge of the magnetic field.
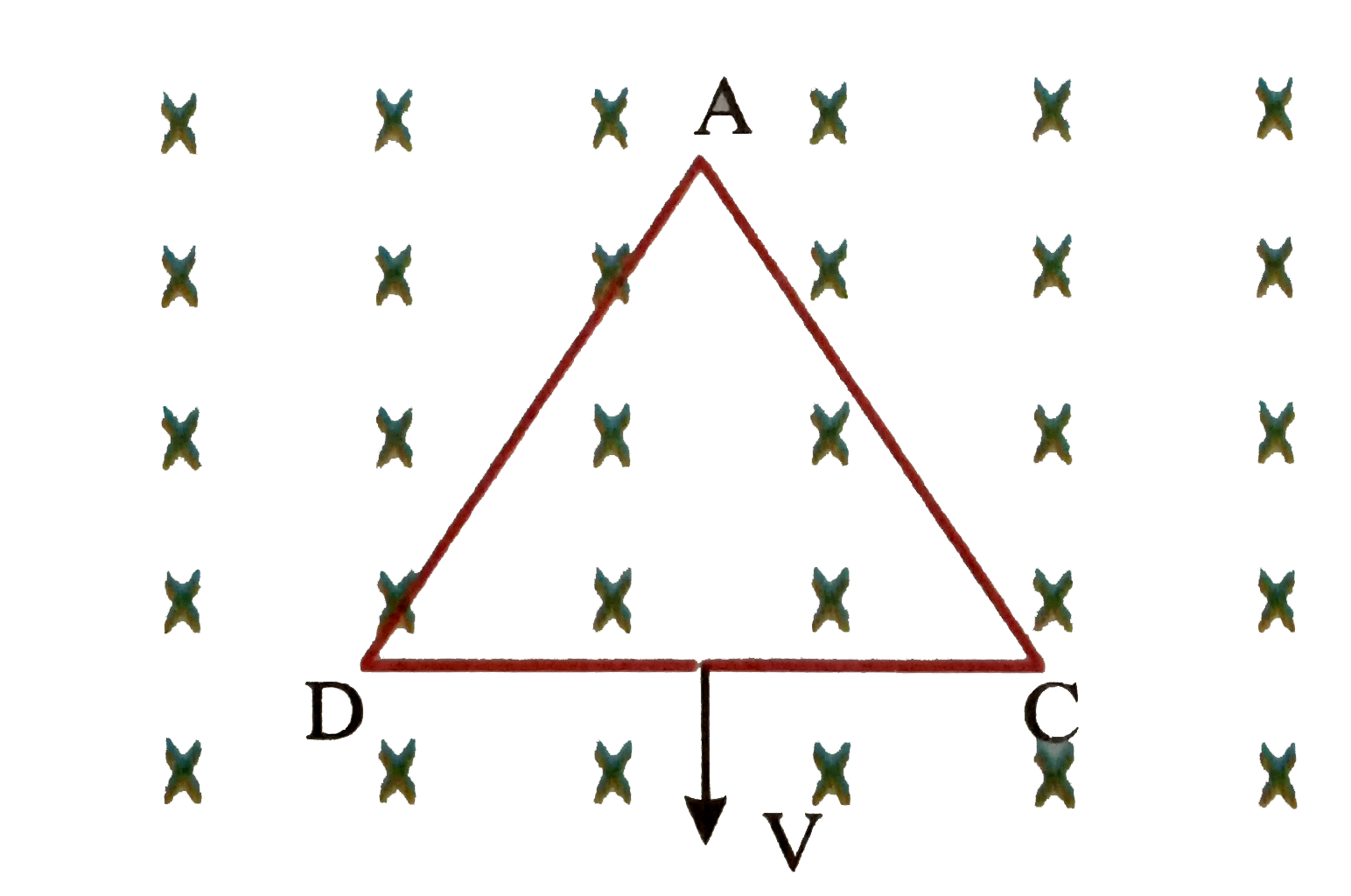
The induced current (i) versus time (t) graph will be as
View SolutionA rectangular, a square , a circular and an elliptical loop, all in the (x−y) plane, are moving out of a uniform magnetic field with a constant velocity →v=vˆi . The magnetic field is directed along the negative z-axis direction. The induced emf, during the passage of these loops , out of the field region, will not remain constant for :
View SolutionA rectangular loop and a circular loop are moving out of a uniform magnetic field to a field-free region with a constant velocity 'v' as shown in the figure . Explain the which loop do you expect the induced emf to the constant during the passage out of the field region . The magnetic field is normal to the loops .
View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
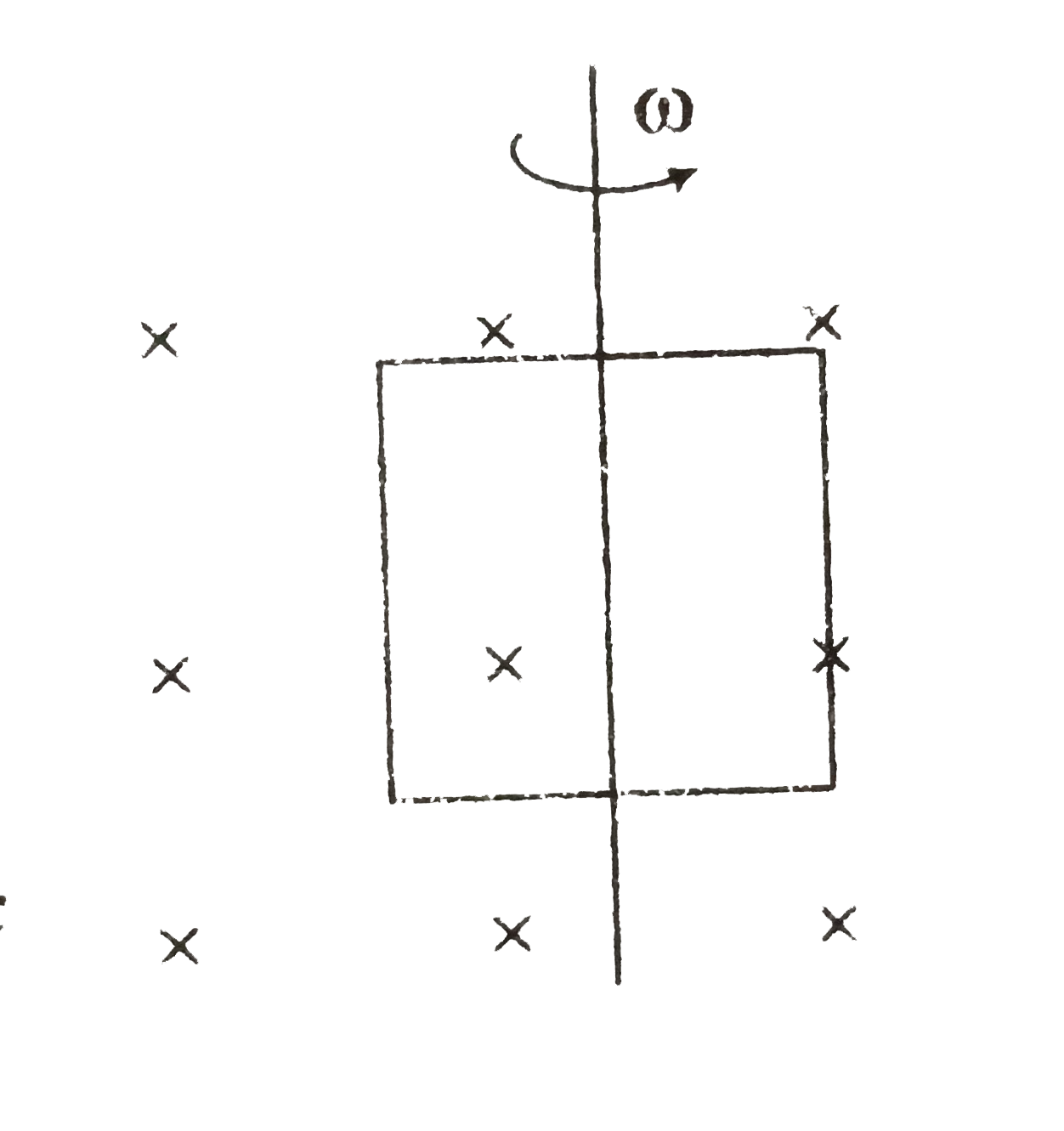
View SolutionRadius ol a circular luop placed in a perpendicular uniform magnetic field is increasing at a constant rate of roms1. If at any instant radius of the loop is r, then emf induced in the loop at that instant will be
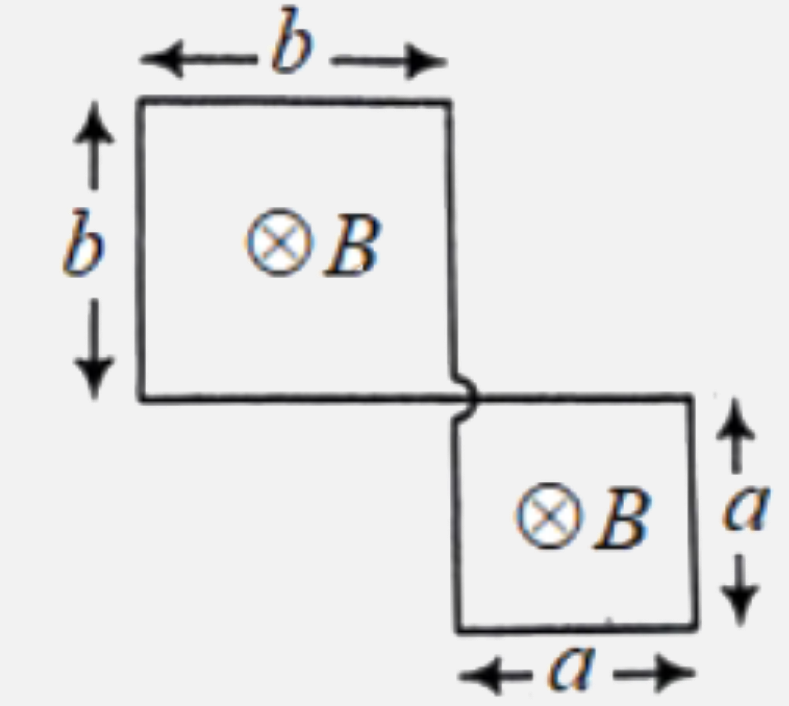
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is

View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
View SolutionFig. Show a rectangular loop MNOP being pulled out of a magnetic field with a uniform velocity v by applying an external force F. The length MN is equal to l and the total resistance of the loop is R. Find(a) the current in the loop,(b) the magnetic force on the loop, (c) the external force F needed to maintain the velocity, (d) the power delivered by the external force and (e) the thermal power developed in the loop.

View Solution
