A close loop is placed in a time-varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the wire radius halved keeping the radius of the loop unchanged, the electrical power dissipated would be :
halved
the same
doubled
quadrupled
The correct Answer is:B
To solve the problem step by step, we need to analyze how the changes in the number of turns and the wire radius affect the electrical power dissipated in the loop placed in a time-varying magnetic field.
Step 1: Understand the Power Dissipation Formula
The electrical power P dissipated in the coil can be expressed as:
P=E2R
where E is the induced EMF and R is the resistance of the coil.
Step 2: Calculate the Induced EMF
The induced EMF E in the coil due to a changing magnetic field is given by:
E=−dΦdt
where Φ is the magnetic flux through the coil. For a coil with n turns, the magnetic flux is:
Φ=n⋅B⋅A
where A is the area of the loop and B is the magnetic field.
Step 3: Area of the Loop
The area A of the loop is given by:
A=πR2
where R is the radius of the loop.
Step 4: Resistance of the Wire
The resistance R of the wire can be calculated using:
R=ρLAw
where ρ is the resistivity of the wire material, L is the length of the wire, and Aw is the cross-sectional area of the wire. The cross-sectional area of the wire with radius r is:
Aw=πr2
Step 5: Changes in Parameters
1. The number of turns n is quadrupled: n′=4n.
2. The radius of the wire is halved: r′=r2.
Step 6: New Resistance Calculation
The new length of the wire L′ when the number of turns is quadrupled is:
L′=4L
The new cross-sectional area of the wire becomes:
A′w=π(r2)2=πr24
Thus, the new resistance R′ is:
R′=ρL′A′w=ρ(4L)πr24=16ρLπr2=16R
Step 7: New Induced EMF Calculation
The new induced EMF E′ becomes:
E′=−dΦ′dt=−d(n′⋅B⋅A)dt=−d(4n⋅B⋅A)dt=4E
Step 8: New Power Calculation
Now substituting the new values into the power formula:
P′=(E′)2R′=(4E)216R=16E216R=E2R=P
Conclusion
The new electrical power dissipated P′ remains the same as the original power P.
Final Answer
The electrical power dissipated would remain the same.
---
The electrical power P dissipated in the coil can be expressed as:
P=E2R
where E is the induced EMF and R is the resistance of the coil.
The induced EMF E in the coil due to a changing magnetic field is given by:
E=−dΦdt
where Φ is the magnetic flux through the coil. For a coil with n turns, the magnetic flux is:
Φ=n⋅B⋅A
where A is the area of the loop and B is the magnetic field.
The area A of the loop is given by:
A=πR2
where R is the radius of the loop.
The resistance R of the wire can be calculated using:
R=ρLAw
where ρ is the resistivity of the wire material, L is the length of the wire, and Aw is the cross-sectional area of the wire. The cross-sectional area of the wire with radius r is:
Aw=πr2
1. The number of turns n is quadrupled: n′=4n.
2. The radius of the wire is halved: r′=r2.
The new length of the wire L′ when the number of turns is quadrupled is:
L′=4L
The new cross-sectional area of the wire becomes:
A′w=π(r2)2=πr24
Thus, the new resistance R′ is:
R′=ρL′A′w=ρ(4L)πr24=16ρLπr2=16R
The new induced EMF E′ becomes:
E′=−dΦ′dt=−d(n′⋅B⋅A)dt=−d(4n⋅B⋅A)dt=4E
Now substituting the new values into the power formula:
P′=(E′)2R′=(4E)216R=16E216R=E2R=P
The new electrical power dissipated P′ remains the same as the original power P.
The electrical power dissipated would remain the same.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A short-circuited coil is placed in a time-varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the wire radius halved, the electrical power dissipated would be
View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.
View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionA thin wire carrying current i is bent to form a closed loop of one turn. The loop is placed in y-z plane with centre at origin. If R is the radius of the loop, then
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
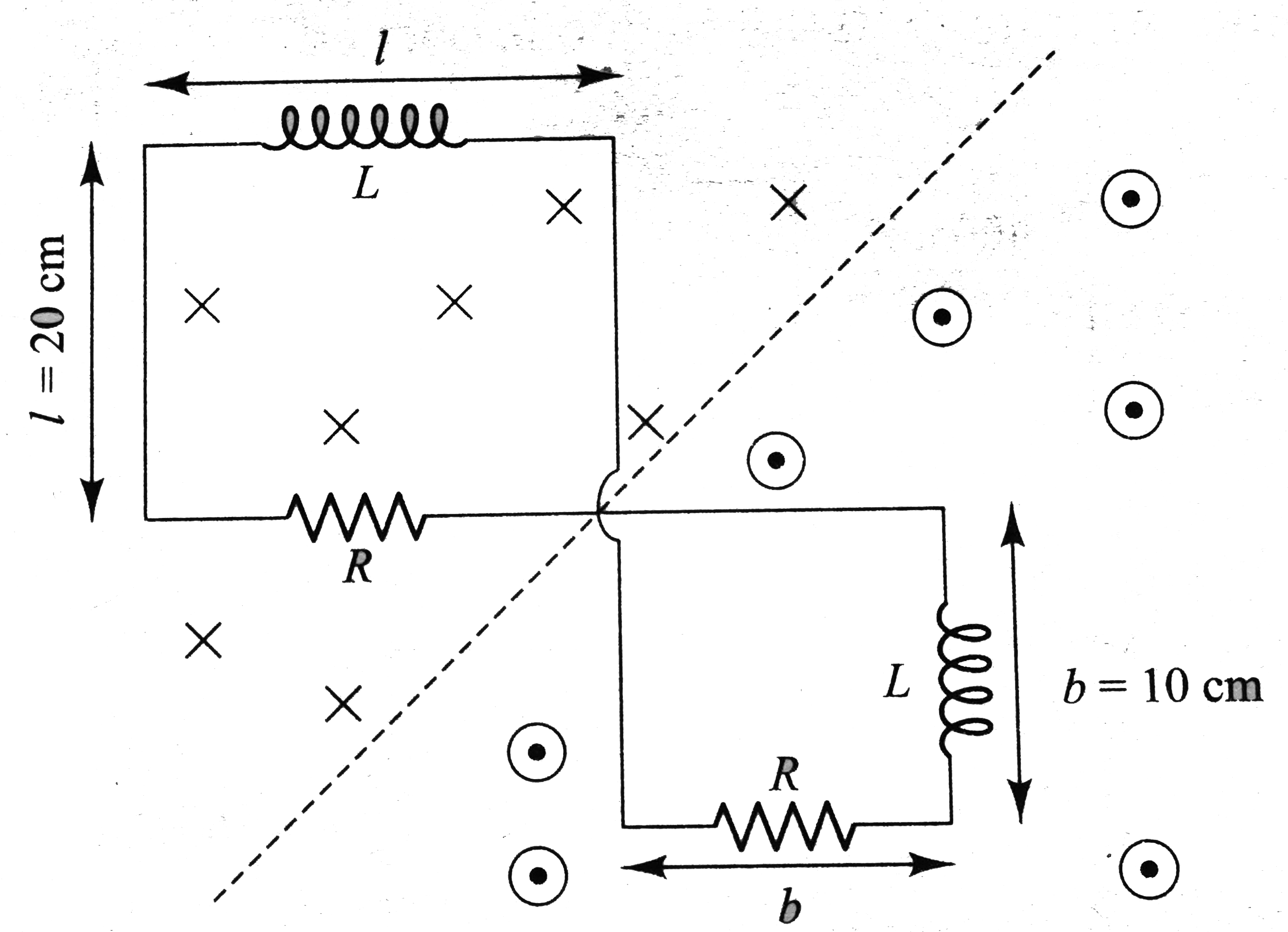
The direction in induced current in the bigger loop will be
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
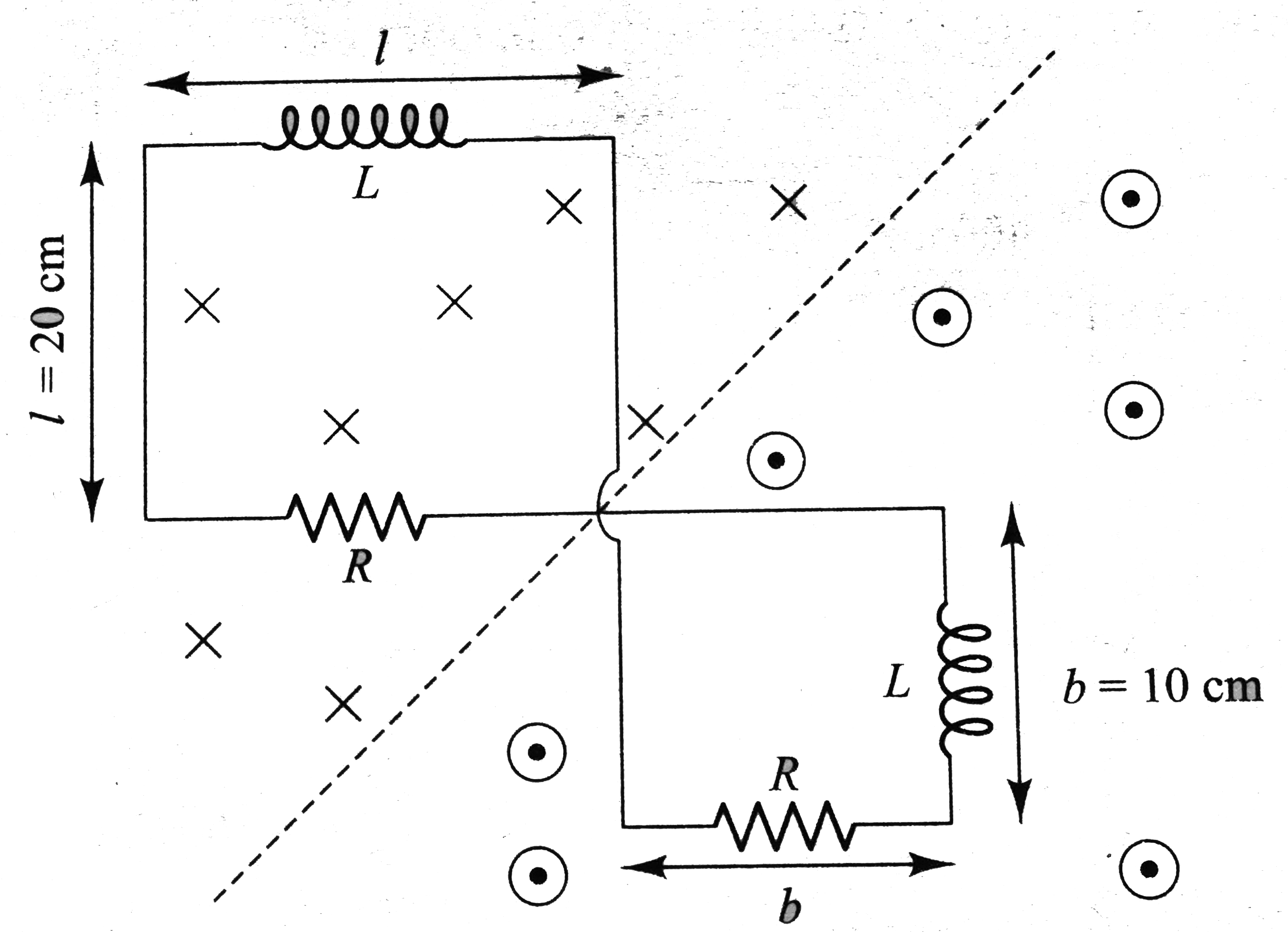
The current in the frame as a funtion of time will be
View SolutionAn external magnetic field is decreased to zero, due to which a current is induced in a circular wire loop of radius r and resistance R placed in the field. This current will not become zero at the instant when B stops changing
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
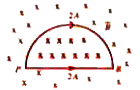
View SolutionA circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
View Solution
