What is the r.m.s. value of an alternating current which when passed through a resistor produces heat which is thrice of that produced by a direct current of 2 amperes in the same resistor?
6 ampere
2 ampere
2√3 ampere
0.65 ampere
The correct Answer is:C
To solve the problem, we need to find the root mean square (r.m.s.) value of an alternating current (AC) that produces heat in a resistor, which is three times the heat produced by a direct current (DC) of 2 amperes.
1. Understanding Heat Produced by DC:
The heat produced by a direct current (I_dc) in a resistor (R) over time (t) is given by the formula:
HDC=I2DC⋅R⋅t
Given that IDC=2A, we can calculate:
HDC=(2A)2⋅R⋅t=4R⋅t
2. Heat Produced by AC:
The heat produced by an alternating current (I_rms) in the same resistor is given by:
HAC=I2rms⋅R⋅t
3. Relationship Between Heat Produced:
According to the problem, the heat produced by the AC is three times that produced by the DC:
HAC=3⋅HDC
Substituting the expression for HDC:
HAC=3⋅(4R⋅t)=12R⋅t
4. Setting the Heat Equations Equal:
Now we can set the equations for heat produced by AC and DC equal to each other:
I2rms⋅R⋅t=12R⋅t
5. Simplifying the Equation:
Since R and t are common in both sides of the equation, we can cancel them out (assuming R and t are not zero):
I2rms=12
6. Finding the r.m.s. Value:
Taking the square root of both sides gives us:
Irms=√12=2√3A
Final Answer:
The r.m.s. value of the alternating current is 2√3A.
---
The heat produced by a direct current (I_dc) in a resistor (R) over time (t) is given by the formula:
HDC=I2DC⋅R⋅t
Given that IDC=2A, we can calculate:
HDC=(2A)2⋅R⋅t=4R⋅t
The heat produced by an alternating current (I_rms) in the same resistor is given by:
HAC=I2rms⋅R⋅t
According to the problem, the heat produced by the AC is three times that produced by the DC:
HAC=3⋅HDC
Substituting the expression for HDC:
HAC=3⋅(4R⋅t)=12R⋅t
Now we can set the equations for heat produced by AC and DC equal to each other:
I2rms⋅R⋅t=12R⋅t
Since R and t are common in both sides of the equation, we can cancel them out (assuming R and t are not zero):
I2rms=12
Taking the square root of both sides gives us:
Irms=√12=2√3A
The r.m.s. value of the alternating current is 2√3A.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-1
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-2
6 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
The RMS value of AC which when passed through a resistor produces heat, which is twice that produced by a steady current of 1.414A in the same resistor is
View SolutionFind the current through resistor R.
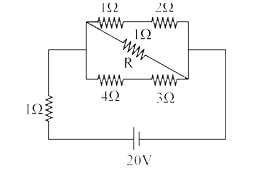
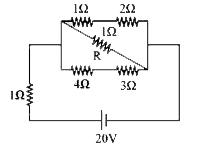
View SolutionFind the current through resistor R
View SolutionThe electric current passes through a metallic wire produces heat because of :
View SolutionIf an AC produces same heat as that produced by a steady current of 4 A , then peak value of current is :
View SolutionWhen a current passes through a resistor, its temperature increases. Is it an adiabatic process?
View SolutionWhat is the approximate peak value of an altemating currrent producing four times the heat produced per second by a steady current of 2 A in a resistor ?
View SolutionFind current passing through the battery and each resistor.

View SolutionIn the figure given below, the current passing through 6Ω resistor is
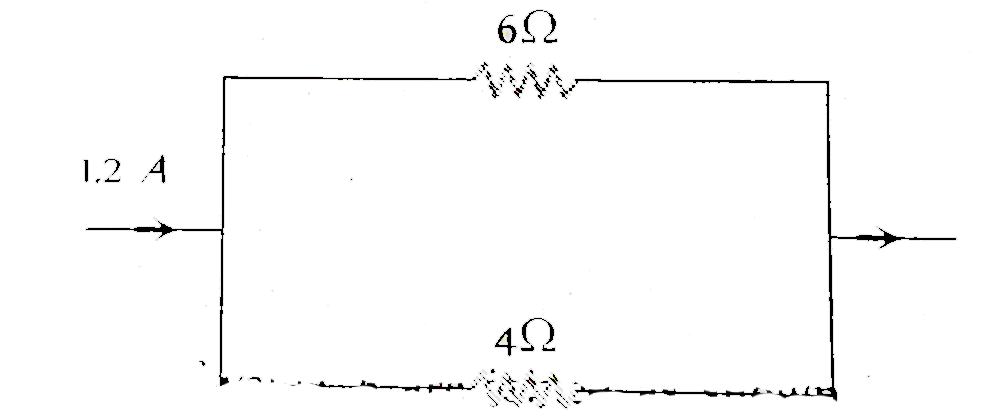
View SolutionFind the value of R in figure so that there is no current in the 50(Omega) resistor.
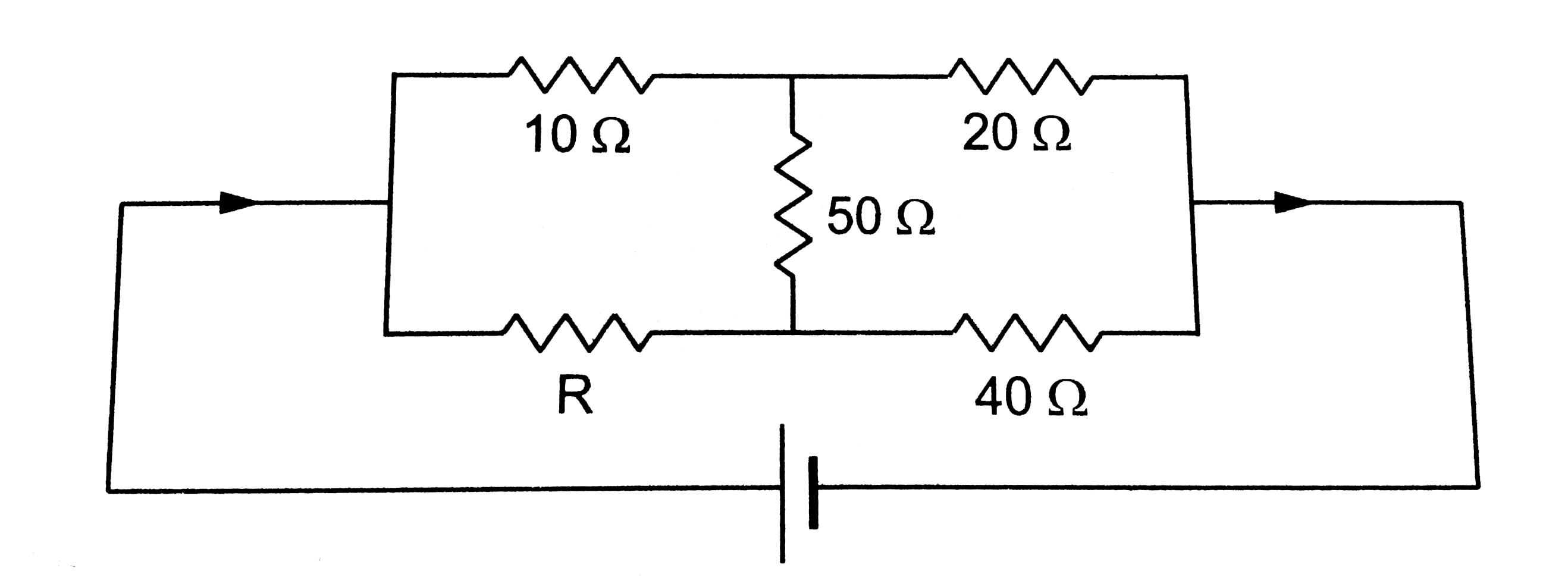
View Solution
