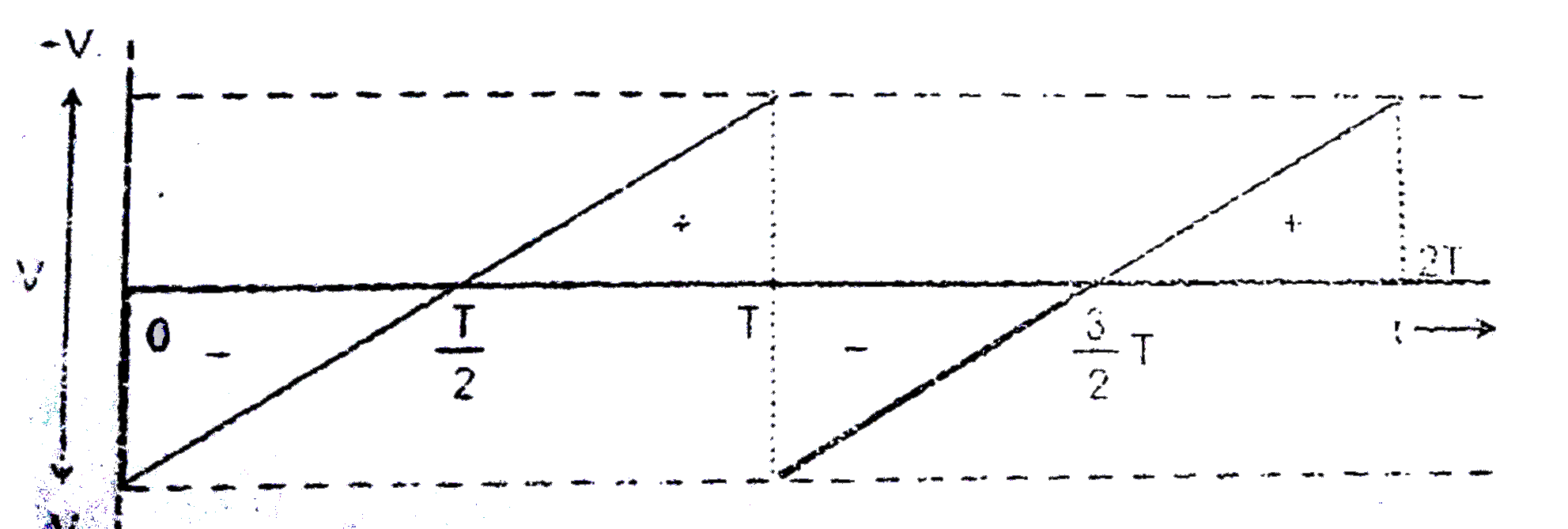
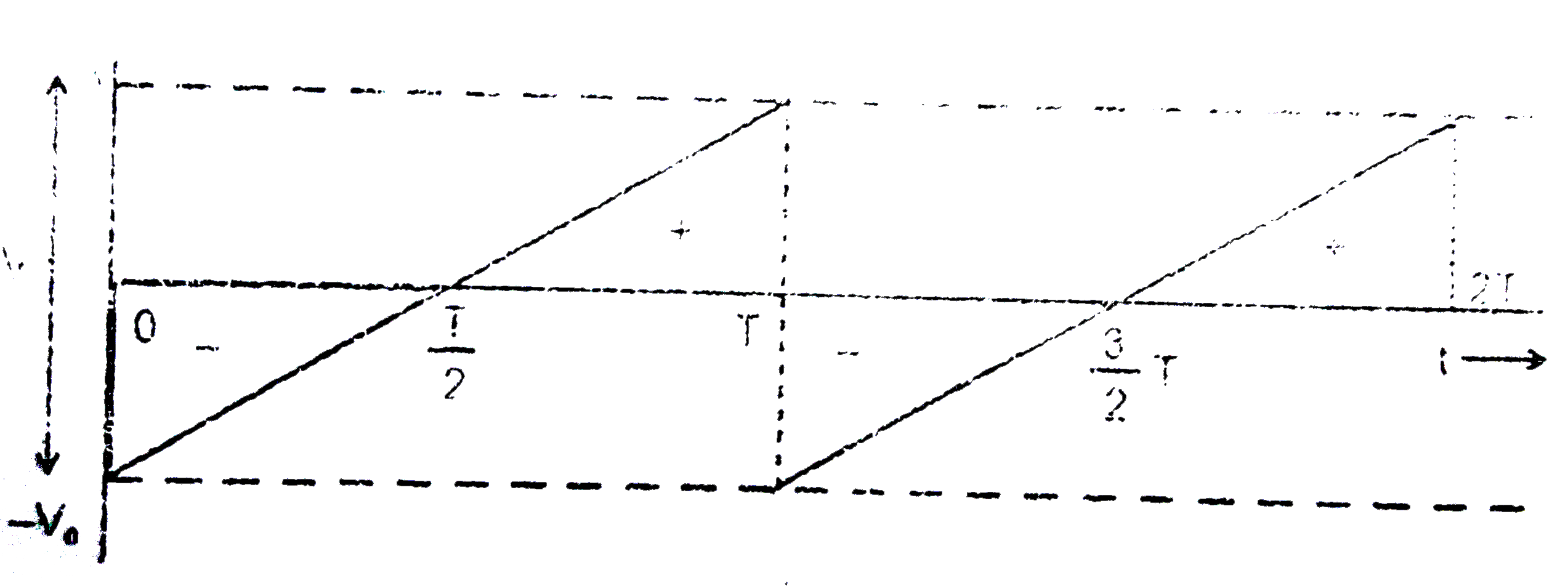
The rms value of the saw-tooth voltage of peak value V0 from t=0 to t=2T as shown in figure is V0√x.Find the value of x.
The correct Answer is:3
General equation of V
V=V∘T/2t−V0=2V0Tt−V0
Vrms=⎡⎢
⎢
⎢
⎢
⎢⎣T∫0V2dtT⎤⎥
⎥
⎥
⎥
⎥⎦12=⎡⎢
⎢
⎢
⎢
⎢⎣T∫0(2V0Tt−V0)2dtT⎤⎥
⎥
⎥
⎥
⎥⎦12=V0√3
x=3
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-3
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-4
11 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-1
14 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
Knowledge Check
The rms value of potential difference V shown in the figure is
 AV0√3BV0CV0√2DV02
AV0√3BV0CV0√2DV02
The average value of a saw-tooth voltage V=V0(2tT−1) Over 0 to T2, (T- time period) is given by
View SolutionThe voltage time (V-t) graoh for triangular wave having peak value (V0) is as shown in fig.The rms value of V in time interval from t=0 to T/4 is:
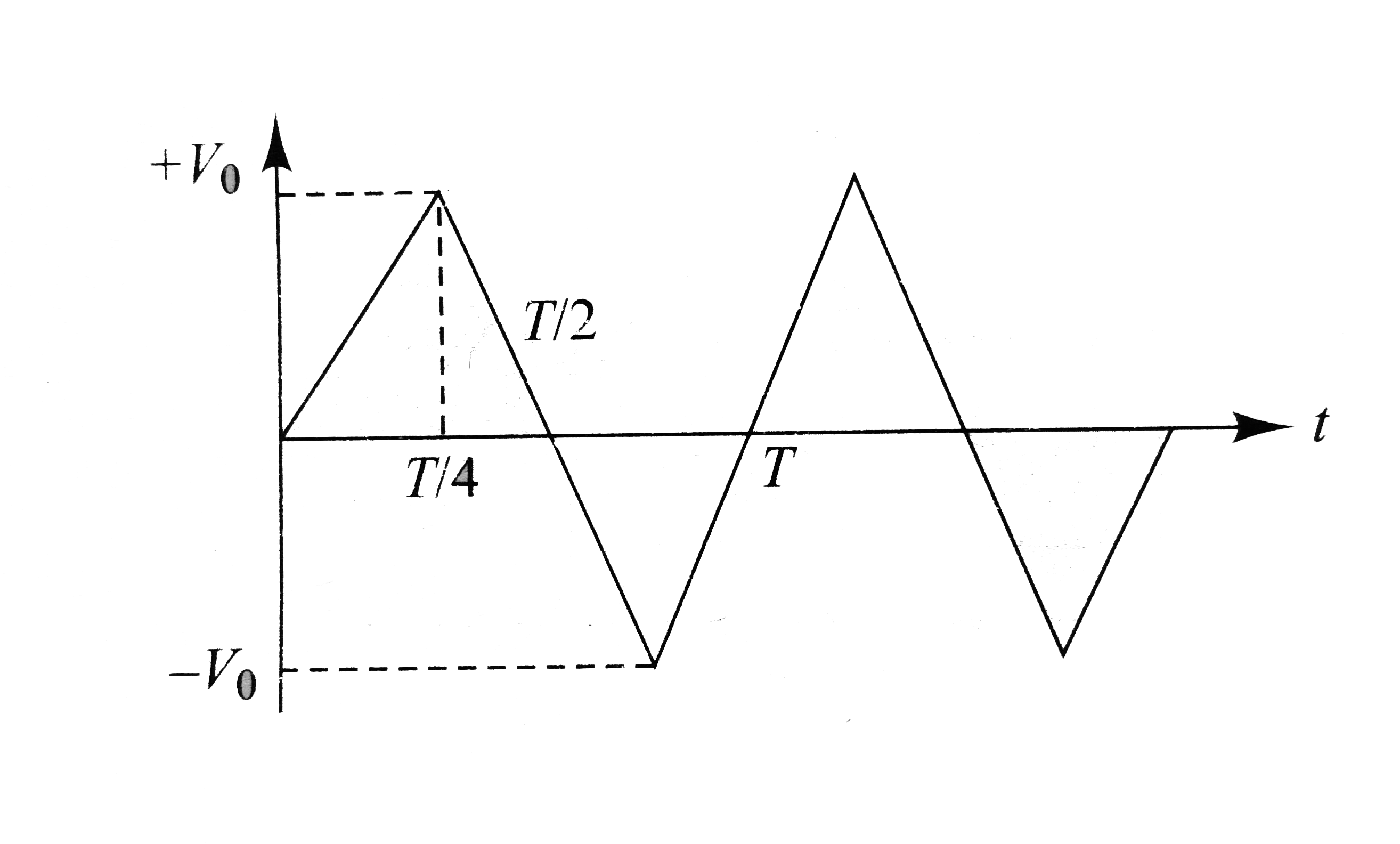
View SolutionThe voltage time (V-t) graoh for triangular wave having peak value (V0) is as shown in fig. The rms value V in time interval t=0 to t=T/4 is
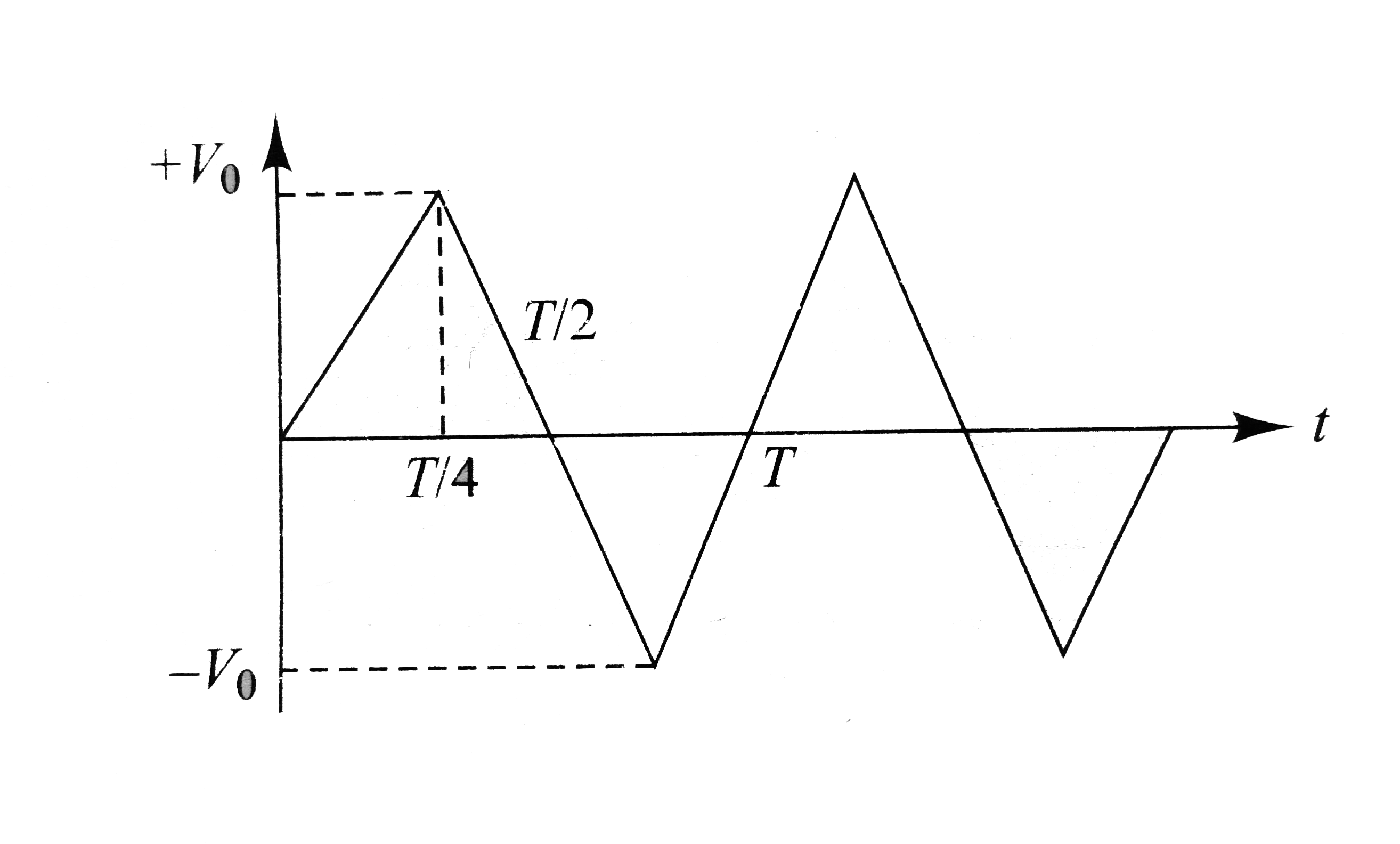
View SolutionFind the rms and the average values of the saw tooth waveform shown in fig.
 .
.
View SolutionFor different values of L, we get different values of T2. The graph between L versus T2 ia as shown in figure. Find the value of 'g' from the given graph.(Take (π)2=10).
 .
.
View SolutionThe average value of an alternating voltage V=V0sinωt over a full cycle is
View SolutionThe average value of an alternating voltage V=V0sinωt over a full cycle is
View Solution