The electric current in an AC circuit is given by I=I0sinωt.What is the time taken by the current to change from its maximum value to the rms value?
The correct Answer is:T/8 or π4ω
To find the time taken by the current in an AC circuit to change from its maximum value to its RMS value, we can follow these steps:
Step 1: Understand the given current equation
The electric current in the AC circuit is given by:
I(t)=I0sin(ωt)
where I0 is the maximum current, and ω is the angular frequency.
Step 2: Determine the maximum current value
The maximum current Imax occurs when sin(ωt)=1:
Imax=I0
Step 3: Determine the RMS value
The RMS (Root Mean Square) value of the current is given by:
Irms=I0√2
Step 4: Set up the equation for the current to equal the RMS value
We need to find the time t1 when the current is at its maximum value and the time t2 when the current equals the RMS value:
I(t2)=Irms
Substituting the RMS value:
I0sin(ωt2)=I0√2
Step 5: Simplify the equation
Dividing both sides by I0 (assuming I0≠0):
sin(ωt2)=1√2
Step 6: Solve for t2
The sine function equals 1√2 at angles:
ωt2=π4andωt2=3π4
Thus, we can express t2 as:
t2=π4ωort2=3π4ω
Step 7: Find the time t1 when the current is maximum
The maximum current occurs at:
ωt1=π2
So,
t1=π2ω
Step 8: Calculate the time difference Δt
The time taken for the current to change from its maximum value to the RMS value is:
Δt=t2−t1
Using the first t2:
Δt=π4ω−π2ω
Finding a common denominator:
Δt=π4ω−2π4ω=−π4ω
This indicates that we should consider the time from maximum to the first occurrence of RMS value:
Δt=π4ω
Final Answer
The time taken by the current to change from its maximum value to its RMS value is:
Δt=T8
where T=2πω is the time period of the AC current.
The electric current in the AC circuit is given by:
I(t)=I0sin(ωt)
where I0 is the maximum current, and ω is the angular frequency.
The maximum current Imax occurs when sin(ωt)=1:
Imax=I0
The RMS (Root Mean Square) value of the current is given by:
Irms=I0√2
We need to find the time t1 when the current is at its maximum value and the time t2 when the current equals the RMS value:
I(t2)=Irms
Substituting the RMS value:
I0sin(ωt2)=I0√2
Dividing both sides by I0 (assuming I0≠0):
sin(ωt2)=1√2
The sine function equals 1√2 at angles:
ωt2=π4andωt2=3π4
Thus, we can express t2 as:
t2=π4ωort2=3π4ω
The maximum current occurs at:
ωt1=π2
So,
t1=π2ω
The time taken for the current to change from its maximum value to the RMS value is:
Δt=t2−t1
Using the first t2:
Δt=π4ω−π2ω
Finding a common denominator:
Δt=π4ω−2π4ω=−π4ω
This indicates that we should consider the time from maximum to the first occurrence of RMS value:
Δt=π4ω
The time taken by the current to change from its maximum value to its RMS value is:
Δt=T8
where T=2πω is the time period of the AC current.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXAMPLE40videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - SOLVED MISCELLANEOUS14videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -3 Part-324videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
Similar Questions
The electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View SolutionA resistance of 20Ω is connected to a source of alternating current rated 110V,50Hz. Find (a) the rms current, (b) the maximum instantaneous current in the resistor and (c) the time taken by the current to change from its maximum value to the rms value.
View SolutionThe alternating current in a circuit is given by I=50sin314t. The peak value and frequency of the current are
View SolutionThe electric current in AC circuit is given by the relation i =3sinωt+4cosωt. The rms value of the current in the circuit in ampere is
View SolutionThe value of current I in the circuit will be
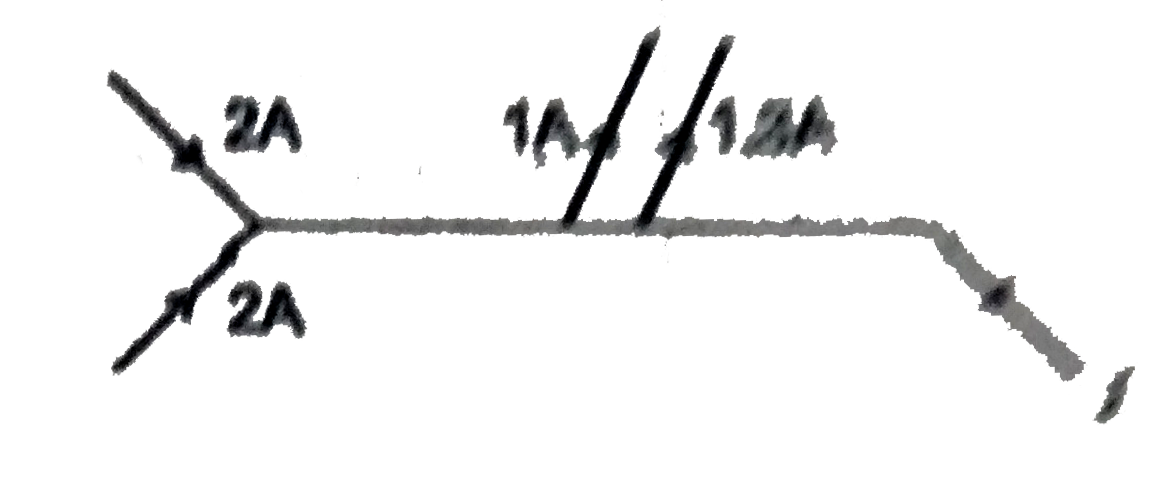 View Solution
View SolutionThe electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s isView SolutionIf instantaneous current in a circuit is given by I=(2+3sinωt) A, then the effective value of resulting current in the circuit is
View SolutionThe current in an AC circuit is given byI=I0 sin (50 π)/t where t is in second. The time interval in which it will reach from zero to its peak value is
View SolutionA resistance of 20ohms is connected to a source of an alternating potential V=220sin(100πt). The time taken by the current to change from its peak value to r.m.s. value is
View Solution

