Two coherent point sources S1andS2 separted by a small distance 'd' are as shown. The fringes obtained on the screen will be :
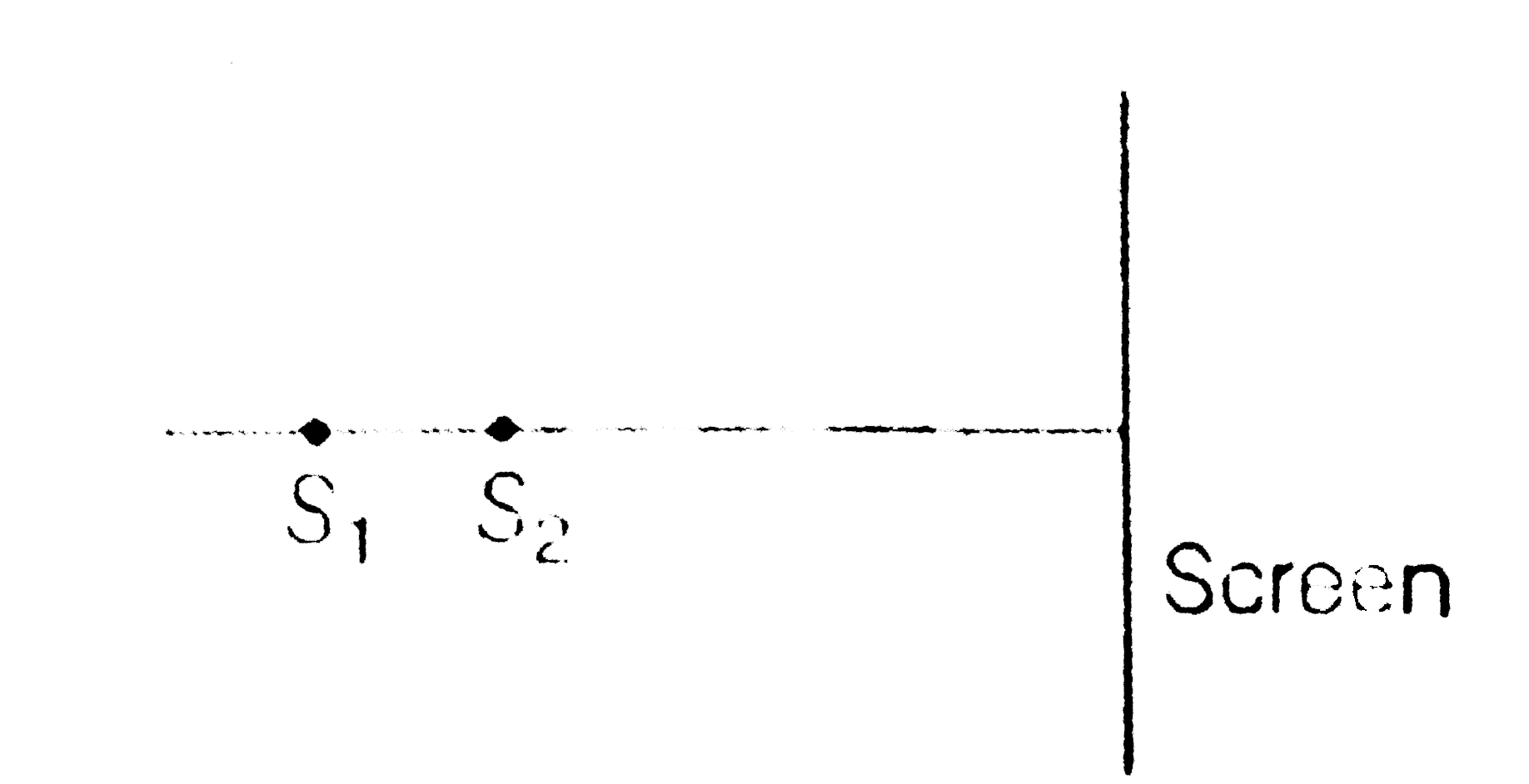
points
straight lines
semi-circles
concentric circles
The correct Answer is:D
It will concentric circles

Topper's Solved these Questions
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-3 (Part-3)
22 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-3 (Part-1)
11 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
Similar Questions
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
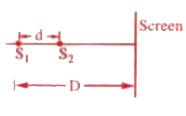
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
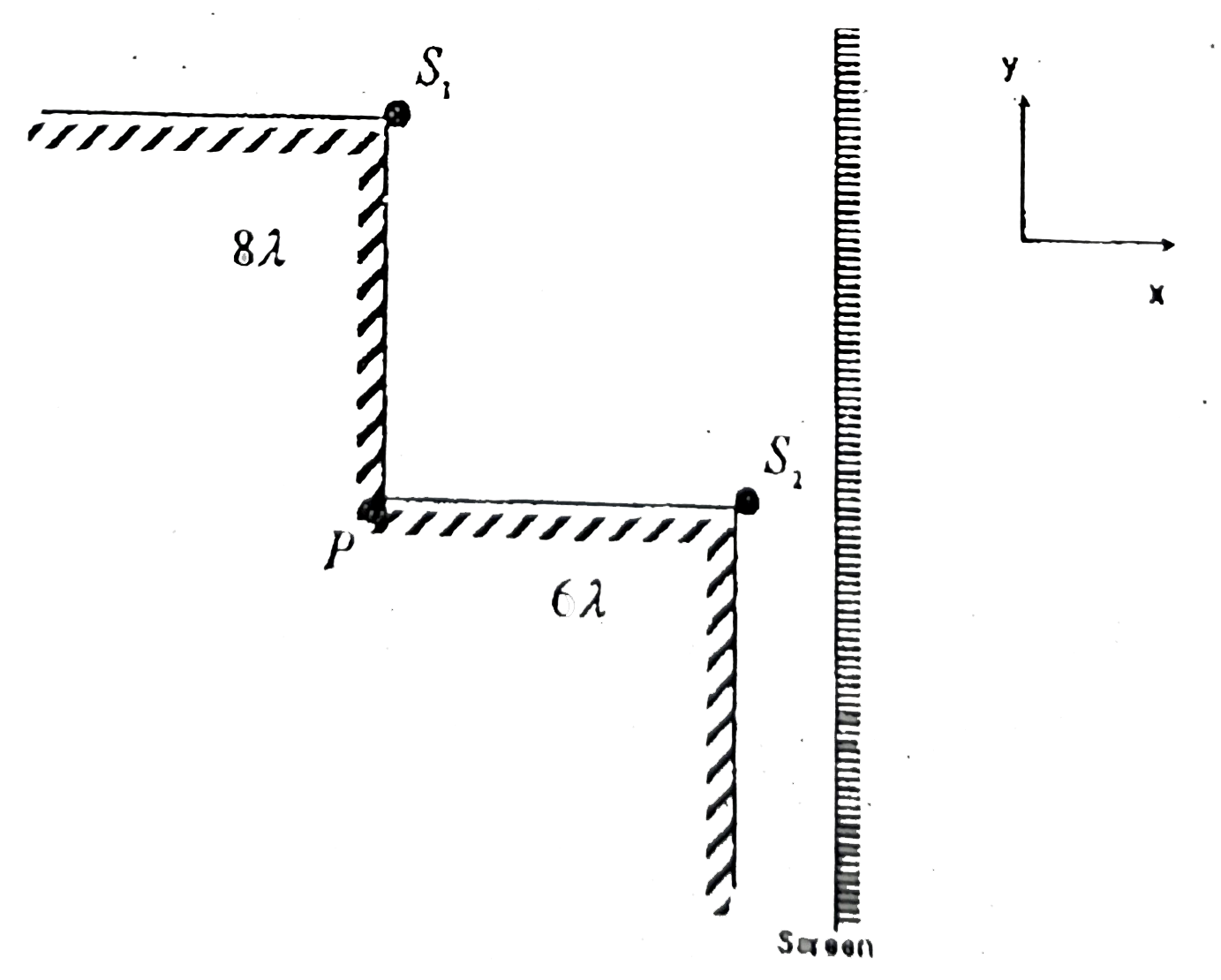
View SolutionTwo coherent sources S1 and S2 are kept on the edges of a step as shown in the figure. An infinitely long screen is placed on the right side of sources and lies at along y−z plane. Calculate total no. of maximas observed on the screen. PS1=8λ and PS2=6λ. Where λ is wavelength of light used. (There is no reflection from steps)
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View Solution
