Two coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
2
3
4
5
The correct Answer is:B
To solve the problem of determining the number of points where maxima are observed when two coherent sources S1 and S2 are separated by a distance of 4λ, we can follow these steps:
Step 1: Understand the Geometry
We have two coherent sources, S1 and S2, separated by a distance d=4λ along the y-axis. A detector moves along the x-axis. The goal is to find the positions along the x-axis where constructive interference (maxima) occurs.
Step 2: Set Up the Problem
Let the distance from the origin (where the sources are located) to the detector be x. The distance from S1 to the detector is S1D and from S2 to the detector is S2D.
Step 3: Calculate Path Difference
The path difference Δ between the waves arriving at the detector from S1 and S2 is given by:
Δ=S2D−S1D
Using the Pythagorean theorem, we can express S1D and S2D in terms of x:
S1D=√x2+(2λ)2(since S1 is at (0,0) and S2 is at (0,4λ))
S2D=√x2+(2λ)2
Step 4: Condition for Maxima
For constructive interference (maxima), the path difference must be an integer multiple of the wavelength:
Δ=nλ(n=0,1,2,…)
Step 5: Substitute and Simplify
Using the path difference, we have:
Δ=S2D−S1D=4λ−0=4λ
Setting this equal to nλ, we can solve for n:
4λ=nλ⟹n=4
Step 6: Determine the Number of Maxima
The values of n can range from 0 to 4 (inclusive), giving us n=0,1,2,3,4. Thus, there are a total of 5 maxima points.
Conclusion
The number of points where maxima are observed is 5.
We have two coherent sources, S1 and S2, separated by a distance d=4λ along the y-axis. A detector moves along the x-axis. The goal is to find the positions along the x-axis where constructive interference (maxima) occurs.
Let the distance from the origin (where the sources are located) to the detector be x. The distance from S1 to the detector is S1D and from S2 to the detector is S2D.
The path difference Δ between the waves arriving at the detector from S1 and S2 is given by:
Δ=S2D−S1D
Using the Pythagorean theorem, we can express S1D and S2D in terms of x:
S1D=√x2+(2λ)2(since S1 is at (0,0) and S2 is at (0,4λ))
S2D=√x2+(2λ)2
For constructive interference (maxima), the path difference must be an integer multiple of the wavelength:
Δ=nλ(n=0,1,2,…)
Using the path difference, we have:
Δ=S2D−S1D=4λ−0=4λ
Setting this equal to nλ, we can solve for n:
4λ=nλ⟹n=4
The values of n can range from 0 to 4 (inclusive), giving us n=0,1,2,3,4. Thus, there are a total of 5 maxima points.
The number of points where maxima are observed is 5.
Similar Questions
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
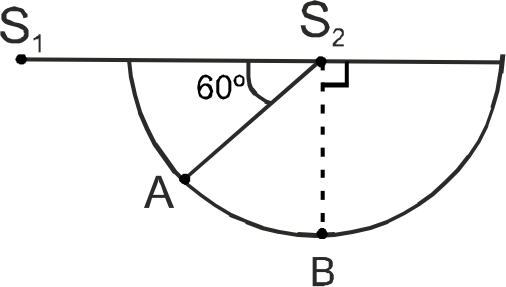
The intensity o sound of B due to S1andS2 is :
View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
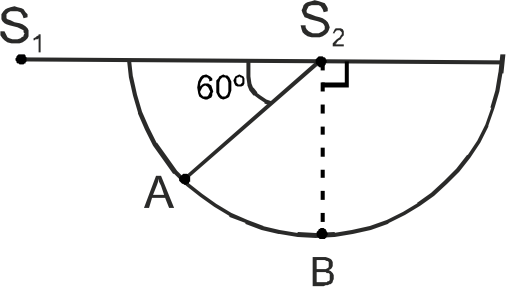
The intensity of sound at B due to S1 only is :
View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
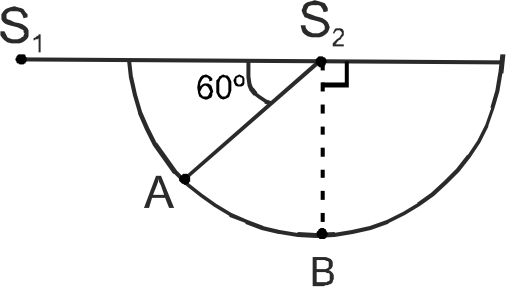
The intensity of sound at A due to S1 only is :
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
View Solution
