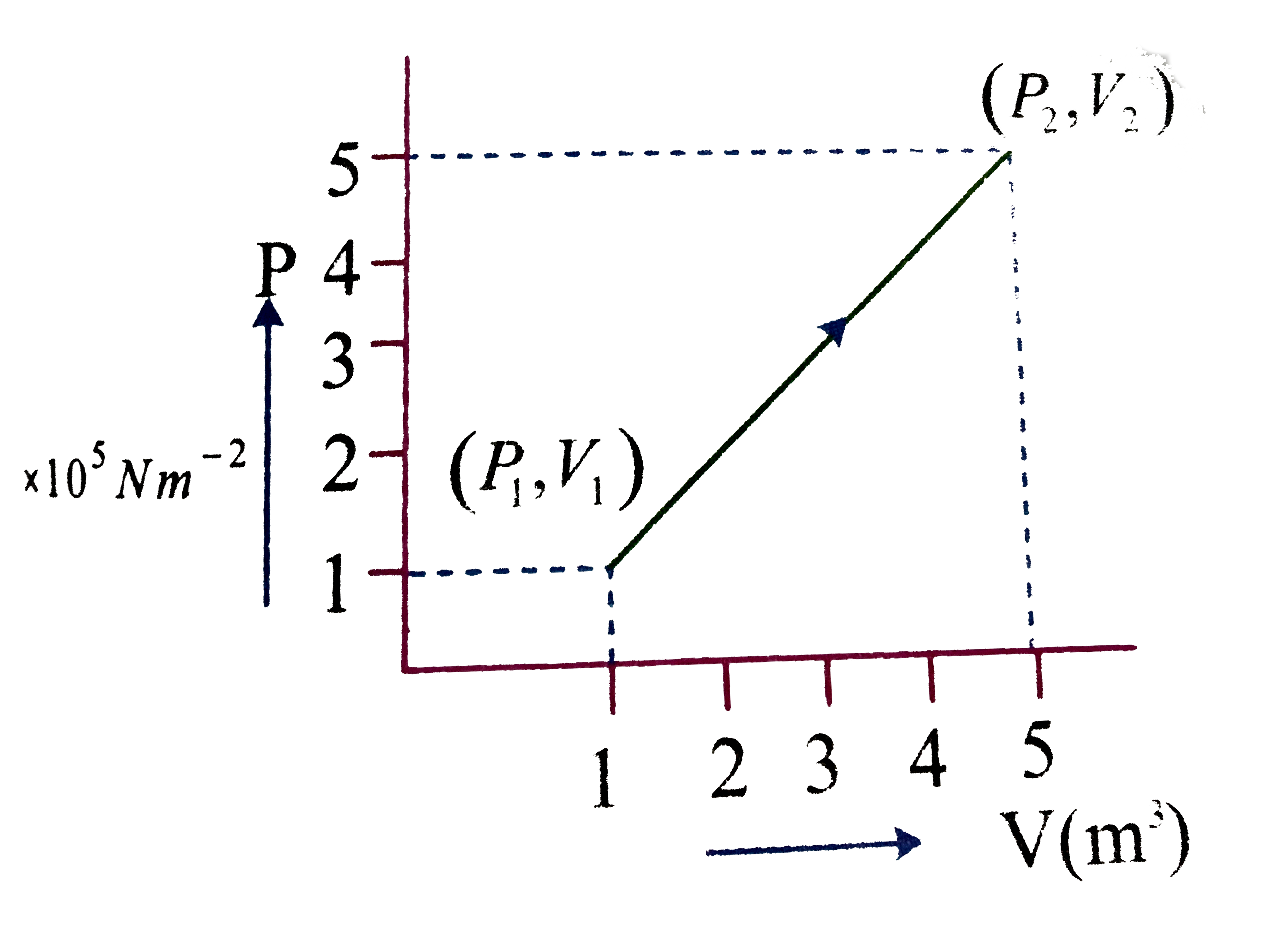
A thermodynamic system goes from states (i) P1,V to 2P1,V (ii) P,V1 to P2,V1. Then work done in the two cases is
Zero,Zero
Zero,−PV1
−PV1, Zero
−PV1,P1V2
The correct Answer is:B
To solve the problem of work done in the two thermodynamic cases, we can follow these steps:
Step 1: Understand the first case
In the first case, the system goes from state (i) P1,V to 2P1,V. Here, the volume remains constant while the pressure changes.
Step 2: Calculate work done in the first case
The work done W in a thermodynamic process is given by the formula:
W=−PexternalΔV
where ΔV is the change in volume. Since the volume does not change in this case (V−V=0), we have:
ΔV=0
Thus, the work done in the first case is:
W1=−Pexternal⋅0=0
Step 3: Understand the second case
In the second case, the system goes from state (ii) P,V1 to P2,V1. Here, the pressure changes while the volume remains constant at V1.
Step 4: Calculate work done in the second case
Again, using the work done formula:
W=−PexternalΔV
In this case, the volume remains constant at V1, so we need to consider the change in volume:
ΔV=Vfinal−Vinitial=V1−V1=0
However, we need to consider the change in volume if we were to change the volume to 2V1 (as indicated in the question). Thus, we can calculate:
W2=−Pexternal(2V1−V1)=−Pexternal⋅V1
Assuming Pexternal=P, we have:
W2=−P⋅V1
Summary of Work Done
- Work done in the first case: W1=0
- Work done in the second case: W2=−P⋅V1
Final Answer
The work done in the two cases is:
1. First case: W1=0
2. Second case: W2=−P⋅V1
In the first case, the system goes from state (i) P1,V to 2P1,V. Here, the volume remains constant while the pressure changes.
The work done W in a thermodynamic process is given by the formula:
W=−PexternalΔV
where ΔV is the change in volume. Since the volume does not change in this case (V−V=0), we have:
ΔV=0
Thus, the work done in the first case is:
W1=−Pexternal⋅0=0
In the second case, the system goes from state (ii) P,V1 to P2,V1. Here, the pressure changes while the volume remains constant at V1.
Again, using the work done formula:
W=−PexternalΔV
In this case, the volume remains constant at V1, so we need to consider the change in volume:
ΔV=Vfinal−Vinitial=V1−V1=0
However, we need to consider the change in volume if we were to change the volume to 2V1 (as indicated in the question). Thus, we can calculate:
W2=−Pexternal(2V1−V1)=−Pexternal⋅V1
Assuming Pexternal=P, we have:
W2=−P⋅V1
- Work done in the first case: W1=0
- Work done in the second case: W2=−P⋅V1
The work done in the two cases is:
1. First case: W1=0
2. Second case: W2=−P⋅V1
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise -2 Part-I: Only one option correct type
23 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 II: Single and double value integer type
16 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - H-1
1 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
Knowledge Check
An ideal non-atomic gas is taken round the cycle ABCDA in the P-V diagram where the coordinates of the points are :
A(P1,V1),B(2P1,V1),C(2P1,2V1) and D(P1,2V1) The work done during the cycle is
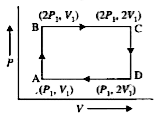 AP1V1B2P1V1C1/2P1V1Dzero
AP1V1B2P1V1C1/2P1V1Dzero
Directions: The following question has four choices out of which ONLY ONE is correct.
A thermodynamical system is changed from state (P1,V1) to (P^², V^²) by two different processes, the quantity which will remain same is:
View SolutionAssertion: When ideal gas expand from P1,V1,T1, to P2,V2,T2 two steps, and work done is high in which number of steps are high
Reason: Work is path function
View Solution_2019_CBT3_E01_051_Q01.png)
A thermodynamic system undergoes two process P1 and P2 from A→B as shown in P−V diagram, choose the correct option.
View SolutionGraphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from (pi,Vi) to (pf,Vf). With the help of a pV plot compare the work done in the above case with that carried out against a constant pressure pf.
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:

Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
wrev>wirr
The works of isothermal and adiabatic processes are different from each other.
wisothermal reversible=2.303nRTlog10(V2V1)
=2.303nRTlog10(P2P1)
wadiabatic reversible=CV(T1−T2)
A thermodynamic system goes in a cyclic process as represented in the following P−V diagram:

The network done during the complete cycle is given by the area
View SolutionAn ideal gas is taken through a series of changes , from P1,V1→4P1,V1→P1,3V1 represented in the figure . The net work done by the gas at the end of the cycle is equal to

View SolutionOne mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View Solution