One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
CV(T1−T2)
CP(T1−T2)
CP+CV2(T1−T2)
(CP−CV)(T1−T2)
The correct Answer is:A
To solve the problem of finding the decrease in internal energy of one mole of hydrogen during an adiabatic expansion, we can follow these steps:
Step 1: Understand the Concept of Internal Energy
The internal energy (U) of an ideal gas is related to its temperature. For an ideal gas, the change in internal energy (ΔU) can be expressed as:
ΔU=nCvΔT
where:
- n = number of moles of the gas
- Cv = molar heat capacity at constant volume
- ΔT = change in temperature
Step 2: Identify the Variables
In this case, we have:
- n=1 mole (as given in the problem)
- Cv for hydrogen (which can be calculated or looked up)
- ΔT=T2−T1 (where T2 is the final temperature and T1 is the initial temperature)
Step 3: Substitute the Values
Since we are looking for the decrease in internal energy, we need to consider that the temperature decreases during adiabatic expansion. Therefore, we can express the change in temperature as:
ΔT=T2−T1
This means:
ΔU=nCv(T2−T1)=1⋅Cv(T2−T1)
Step 4: Account for the Decrease in Internal Energy
Since the problem asks for the decrease in internal energy, we can express this as:
ΔU=Cv(T2−T1)
However, since T2<T1 during the expansion, we can rewrite this as:
ΔU=Cv(T2−T1)=−Cv(T1−T2)
Step 5: Final Expression
Thus, the decrease in internal energy of the gas during this adiabatic process is given by:
ΔU=−Cv(T1−T2)
Conclusion
The final expression for the decrease in internal energy is:
ΔU=Cv(T1−T2)
The internal energy (U) of an ideal gas is related to its temperature. For an ideal gas, the change in internal energy (ΔU) can be expressed as:
ΔU=nCvΔT
where:
- n = number of moles of the gas
- Cv = molar heat capacity at constant volume
- ΔT = change in temperature
In this case, we have:
- n=1 mole (as given in the problem)
- Cv for hydrogen (which can be calculated or looked up)
- ΔT=T2−T1 (where T2 is the final temperature and T1 is the initial temperature)
Since we are looking for the decrease in internal energy, we need to consider that the temperature decreases during adiabatic expansion. Therefore, we can express the change in temperature as:
ΔT=T2−T1
This means:
ΔU=nCv(T2−T1)=1⋅Cv(T2−T1)
Since the problem asks for the decrease in internal energy, we can express this as:
ΔU=Cv(T2−T1)
However, since T2<T1 during the expansion, we can rewrite this as:
ΔU=Cv(T2−T1)=−Cv(T1−T2)
Thus, the decrease in internal energy of the gas during this adiabatic process is given by:
ΔU=−Cv(T1−T2)
The final expression for the decrease in internal energy is:
ΔU=Cv(T1−T2)
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Energy & spring pendulum)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Kinetic theory of gasess)
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
View SolutionAn ideal gas (1 mol, monatomic) is in the intial state P (see Fig.) on an isothermal A at temperature T0. It is brought under a constant volume (2V0) process to Q which lies on an adiabatic B intersecting the isothermal A at (P0,V0,T0). The change in the internal energy of the gas during the process is (in terms of T0)(22/3=1.587)
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
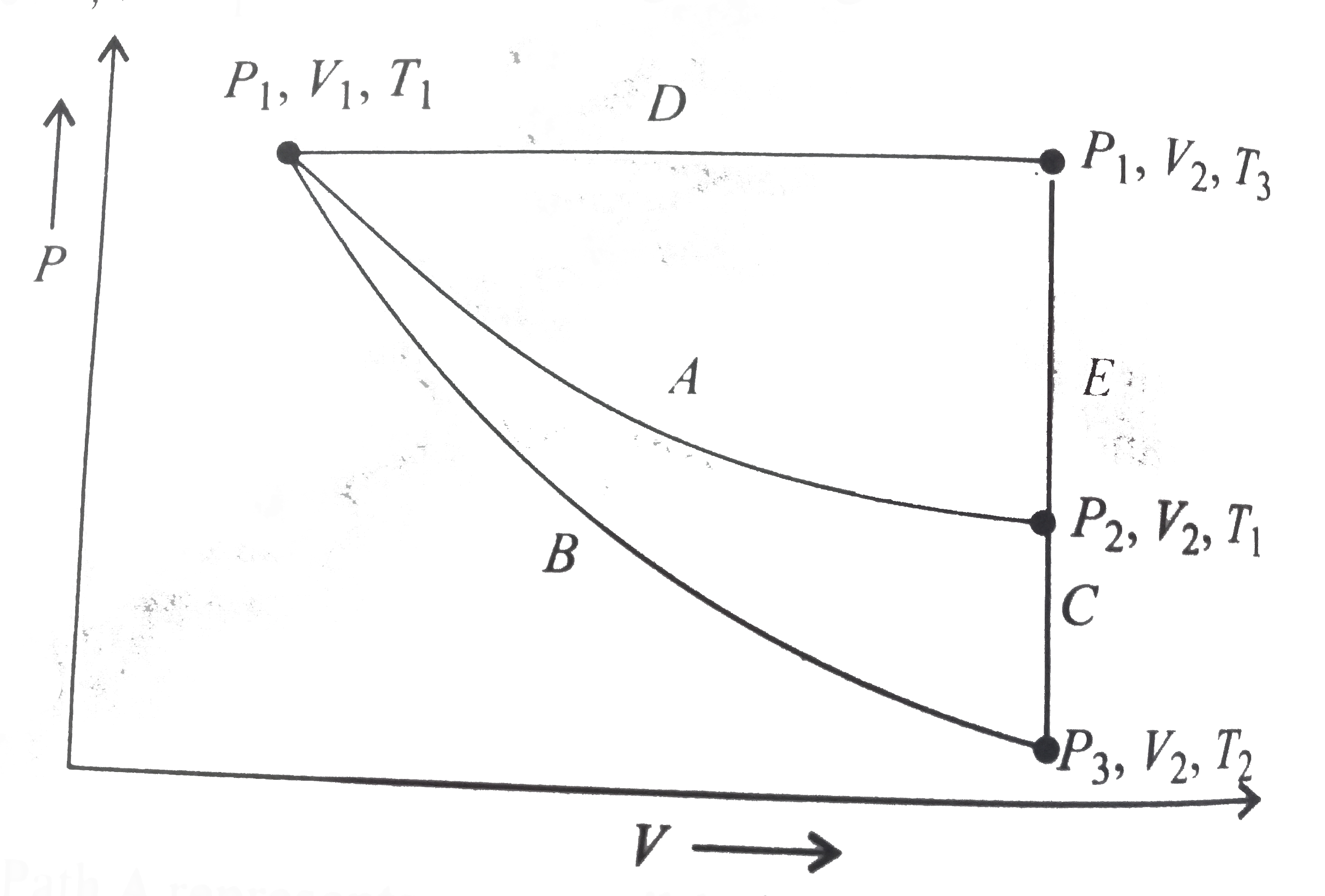
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
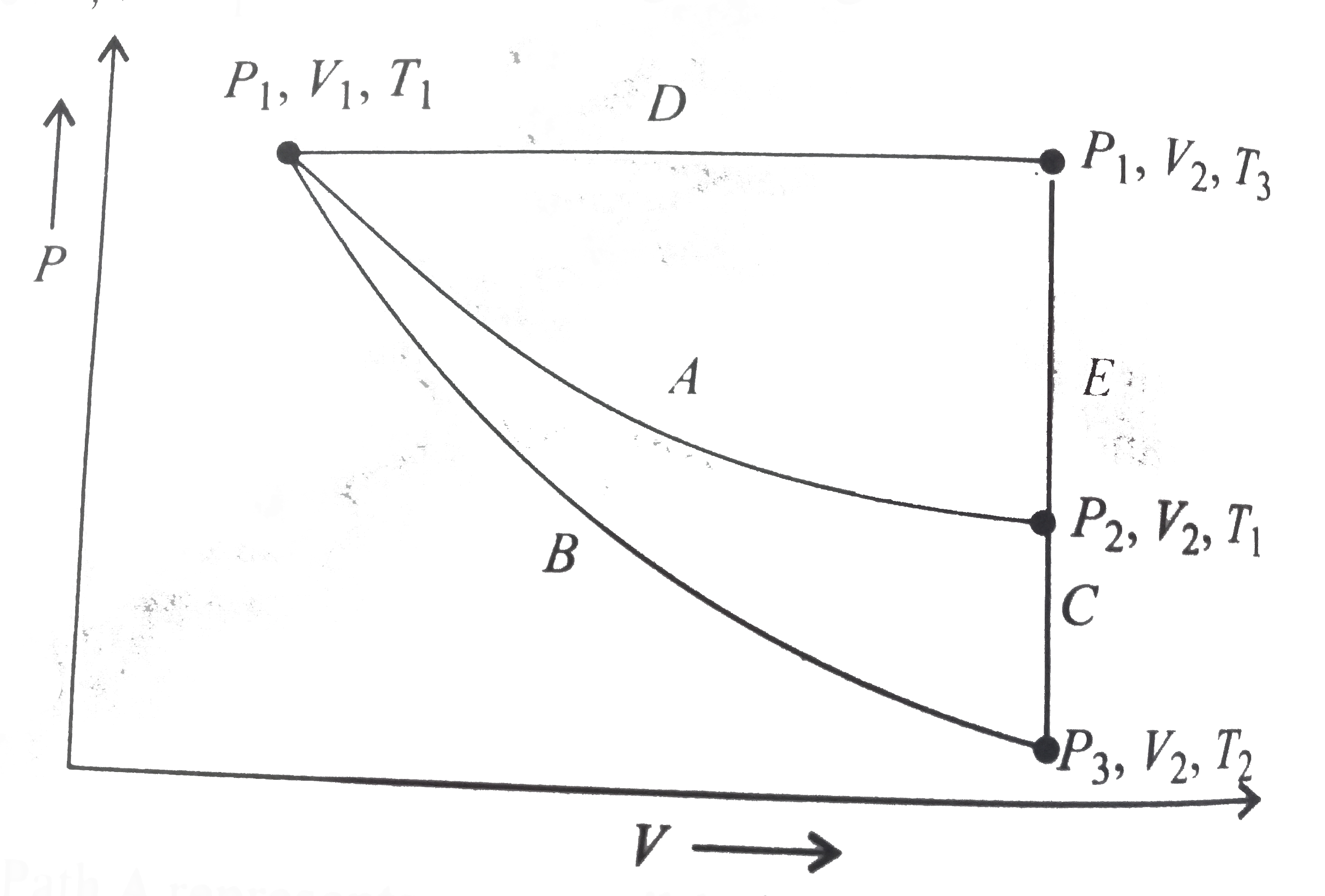
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
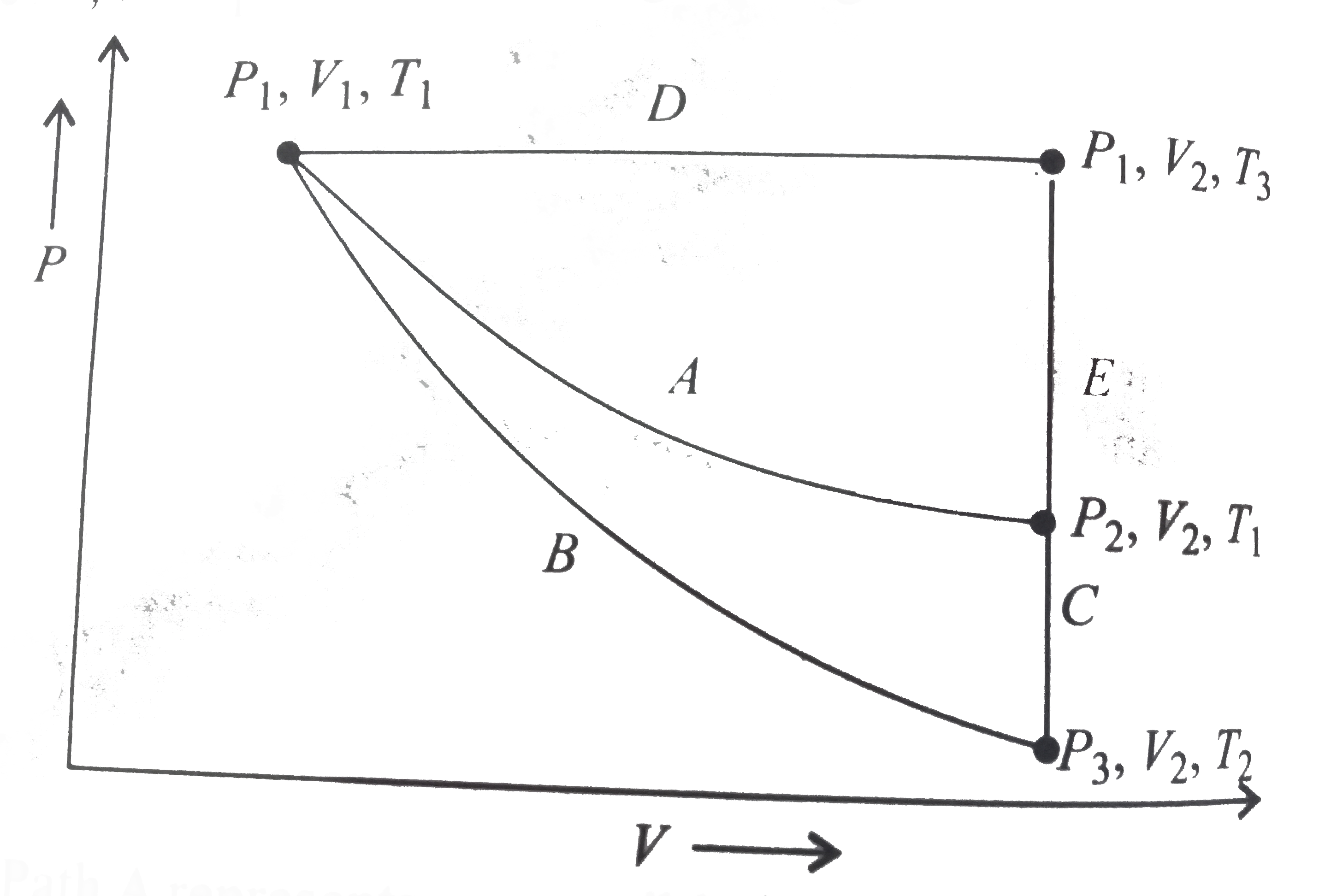
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionAn ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
View SolutionAt 27∘C two moles of an ideal monoatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas, (ii) change in its internal energy, and (iii) the work done by the gas during this process.
View SolutionAn ideal gas (1 mol ,monatomic) is in the initial state P (see diagram) on an isothermal curve A at a temperature T0 . It is brought under a constant volume (2V0) process to Q which lies on an adiabatic curve B intersecting the isothermal curve A at (P0,V0,T0) . The change in the internal energy of the gas (in terms of T0 ) during the process is (22/3=1.587)

View Solution
