Consider the following hypothetical equilibrium
2B(g)⇔B2(g)
If d is observed vapour density and D is theoretical vapour density, then degree of association (α) will be
α=(D−dd)
α=2D−dD
α=2−2Dd
α=2DD−d
The correct Answer is:C
To solve the problem regarding the degree of association (α) for the equilibrium reaction 2B(g)⇌B2(g), we will follow these steps:
Step 1: Write the equilibrium reaction
The given equilibrium reaction is:
2B(g)⇌B2(g)
Step 2: Define the initial moles
Initially, we have 2 moles of B. When the reaction reaches equilibrium, let α be the degree of association. The moles of B that associate to form B2 will be 2α (since 2 moles of B are needed to form 1 mole of B2).
Step 3: Calculate the moles at equilibrium
At equilibrium:
- Moles of B left = Initial moles - Moles that reacted = 2−2α
- Moles of B2 formed = α
Step 4: Total moles at equilibrium
The total moles at equilibrium will be:
Total moles=(2−2α)+α=2−α
Step 5: Relate vapor density to moles
The vapor density (D) is related to the number of moles. The theoretical vapor density D is calculated based on the assumption that there is no association (i.e., all B remains as B):
- Theoretical vapor density D=Molar massTotal moles when no association occurs.
For the initial 2 moles of B, the theoretical vapor density D would be:
D=M2
where M is the molar mass of B.
Step 6: Observed vapor density
The observed vapor density d at equilibrium is given by:
d=MTotal moles at equilibrium=M2−α
Step 7: Use the formula for degree of association
The degree of association α can be calculated using the formula:
α=D−dD
Step 8: Substitute the values
Substituting d and D into the equation:
1. D=M2
2. d=M2−α
Now substituting these into the formula:
α=M2−M2−αM2
Step 9: Simplify the equation
1. Cancel M from numerator and denominator:
α=12−12−α12
2. Simplifying further leads to:
α=1−12−α
Step 10: Solve for α
Cross-multiplying and simplifying will yield the final expression for α:
α=2D−2dd
Final Result
Thus, the degree of association α is given by:
α=2−2dD
The given equilibrium reaction is:
2B(g)⇌B2(g)
Initially, we have 2 moles of B. When the reaction reaches equilibrium, let α be the degree of association. The moles of B that associate to form B2 will be 2α (since 2 moles of B are needed to form 1 mole of B2).
At equilibrium:
- Moles of B left = Initial moles - Moles that reacted = 2−2α
- Moles of B2 formed = α
The total moles at equilibrium will be:
Total moles=(2−2α)+α=2−α
The vapor density (D) is related to the number of moles. The theoretical vapor density D is calculated based on the assumption that there is no association (i.e., all B remains as B):
- Theoretical vapor density D=Molar massTotal moles when no association occurs.
D=M2
where M is the molar mass of B.
The observed vapor density d at equilibrium is given by:
d=MTotal moles at equilibrium=M2−α
The degree of association α can be calculated using the formula:
α=D−dD
Substituting d and D into the equation:
1. D=M2
2. d=M2−α
α=M2−M2−αM2
1. Cancel M from numerator and denominator:
α=12−12−α12
2. Simplifying further leads to:
α=1−12−α
Cross-multiplying and simplifying will yield the final expression for α:
α=2D−2dd
Thus, the degree of association α is given by:
α=2−2dD
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-2 (Part-1)
28 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-2 (Part-2)
22 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-1 (Part-1)
38 Videos
- CHEMICAL BONDINGBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL BONDINGEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
6 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS BOOK - RESONANCE ENGLISHCHAPTER - D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS EXERCISE - Match the column
1 Video
Similar Questions
Consider the following equilibrium
2AB(g)⇔A2(g)+B2(g)
The vapour density of the equilibrium mixture does not depend upon
View SolutionFor the dissociation of PCl5 into PCl3 and Cl2 in gaseous phase reaction , if d is the observed vapour density and D the theoretical vapour density with 'α' as degree of dissociation ,variaton of D/d with 'α' is given by ?
View SolutionFor the dissociation of PCI5 into PCI3andCl2 in gaseous phase reaction, If "d' is the observed vapour density and 'D' theoretical vapour density with 'α' as degree of dissociation. Variation of Dd with 'α' is given by which graph?
View SolutionSO3(g)⇔SO2(g)+12O2(g)
If observed vapour density of mixture at equilibrium is 35 then find out value of α
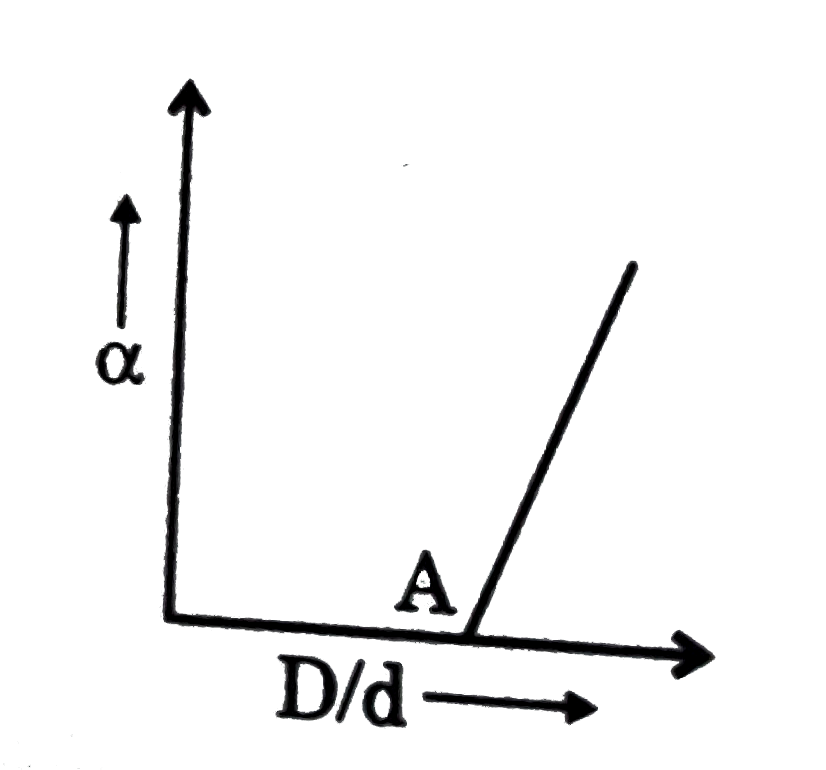
View SolutionBefore equilibrium is set-up the chemical reaction N2O4(g)⇔2NO2(g), vapour density d of the gaseous mixture was measured. If D is the theoretica value of vapour density, variation of α with D/d is given by the graph below. What is value D/d at point A ?
View SolutionFor the following equilibrium reaction ,
N2O4(g)⇔2NO2(g)
NO2 is 50% of total volume at given temperature . Hence vapour density of the equilibrium mixture is
View SolutionAmmonium chloride dissociates as,
NH4Cl(g)⇔NH3(g)+HCl(g)
The vapour density becomes half the initial value when degree of dissociation is 0.5.
View SolutionThe vapour density of PCl5 at 43K is is found to be 70.2. Find the degree of dissociation of PCl5 at this temperature.
View SolutionConsider the following equilibrium
PCl5(g)⇔PCl3(g)+Cl2(g) in a closed container. At a fixed temperature, the volume of the reaction container is halved. For this change, which of the following statements holds true regarding the equilibrium constant (Kp) and degree of dissocitation (α) ?
View SolutionConsider the following equilibrium in a closed container:
N2O4(g)⇔2NO2(g)
At a fixed temperature, the volume of the reaction container is halved. For this change which of the following statements holds true regarding the equilibrium constant (Kp) and the degree of dissociation (α)?
View Solution