SO3(g)⇔SO2(g)+12O2(g)
If observed vapour density of mixture at equilibrium is 35 then find out value of α
0.28
0.38
0.48
0.58
The correct Answer is:A
To solve the problem, we need to find the degree of dissociation (α) of the reaction:
SO3(g)⇌SO2(g)+12O2(g)
Given that the observed vapor density of the mixture at equilibrium is 35, we can use the formula for degree of dissociation:
α=D−d(n−1)⋅d
Where:
- D = Molar mass of the reactant (SO3) / 2
- d = Vapor density at equilibrium
- n = Number of moles of products formed from 1 mole of reactant
Step 1: Calculate the molar mass of SO3
The molar mass of SO3 can be calculated as follows:
- Molar mass of Sulfur (S) = 32 g/mol
- Molar mass of Oxygen (O) = 16 g/mol
Thus, the molar mass of SO3 is:
Molar mass of SO3=32+(16×3)=32+48=80 g/mol
Step 2: Calculate D
Now, we can calculate D:
D=Molar mass of SO32=802=40
Step 3: Identify d
The vapor density at equilibrium is given as:
d=35
Step 4: Calculate n
Next, we need to find n. For the reaction, starting with 1 mole of SO3, the products formed are:
- 1 mole of SO2
- 0.5 mole of O2
Thus, the total number of moles of products is:
n=1+0.5=1.5
Step 5: Substitute values into the equation for α
Now we can substitute the values into the equation for α:
α=D−d(n−1)⋅d=40−35(1.5−1)⋅35
Calculating the numerator:
40−35=5
Calculating the denominator:
(1.5−1)⋅35=0.5⋅35=17.5
Now substituting these values back into the equation for α:
α=517.5=0.2857≈0.28
Final Answer
Thus, the value of α is approximately:
α≈0.28
- D = Molar mass of the reactant (SO3) / 2
- d = Vapor density at equilibrium
- n = Number of moles of products formed from 1 mole of reactant
The molar mass of SO3 can be calculated as follows:
- Molar mass of Oxygen (O) = 16 g/mol
Now, we can calculate D:
The vapor density at equilibrium is given as:
Next, we need to find n. For the reaction, starting with 1 mole of SO3, the products formed are:
- 0.5 mole of O2
Now we can substitute the values into the equation for α:
Thus, the value of α is approximately:
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-2 (Part-1)
28 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-2 (Part-2)
22 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-1 (Part-1)
38 Videos
- CHEMICAL BONDINGBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL BONDINGEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
6 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS BOOK - RESONANCE ENGLISHCHAPTER - D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS EXERCISE - Match the column
1 Videos
Similar Questions
At 627∘ C and one atmosphere SO3 is is partially dissociated into SO2andO2 by SO3(g)⇔SO2(g)+12O2(g). The density of the equilibrium mixture is 0.925 g/litre. What is the degree of dissociation ?
View SolutionAt 627∘C and 1 atm SO3 is partially dissociated into SO2 and O2 by the reaction
SO3(g)⇔SO2(g)+1/2O2(g)
The density of the equilibrium mixture is 0.925gL−1. What is the degree of dissociation?
View SolutionAt 727∘C and 1.2atm of total equilibrium pressure, SO3 is partially dissociated into SO2 and O2 as:
SO3(g)⇔SO2(g)+12O2(g)
The density of equilibrium mixture is 0.9g/L. The degree of dissociation is:, [UseR=0.08atmLmol−1K−1]
View SolutionBefore equilibrium is set-up the chemical reaction N2O4(g)⇔2NO2(g), vapour density d of the gaseous mixture was measured. If D is the theoretica value of vapour density, variation of α with D/d is given by the graph below. What is value D/d at point A ?
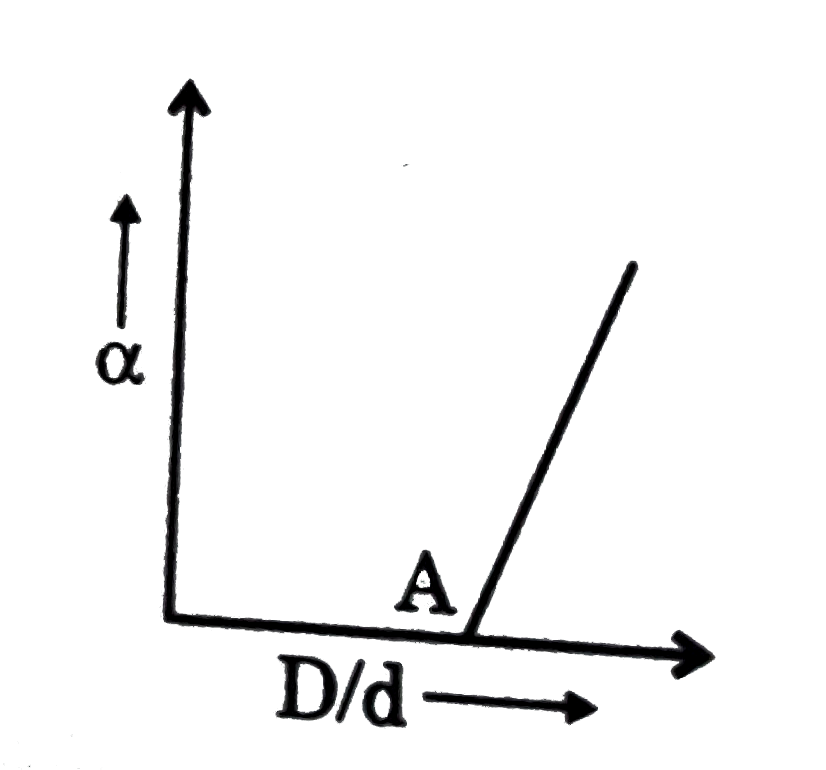
View SolutionSO3(g)+CO(g)⇔SO2(g)+CO2(g)
Which of the following activity can reduce the equilibrium concentration of CO to half?
View SolutionFor the reaction N2O(g)⇔2NO2(g).ΔH=57.49kJ/ mole, the vapour density of equilibrium mixture ……………………….. with increase of temperature.
View SolutionCaCO3(s)⇔CaO(s)+CO2(g)
CO2(g)⇔CO(g)+12O2(g)
For above simultaneous equilibrium if CO2 is added from out side at equilibrium then:
View SolutionFor the equlibrium SO3(g)⇔SO2(g)+12O(2)(g) the molar mass at equlibrium was observed to be 60. then the degree of dissociation of SO3 would be
View SolutionConsider the following equilibrium
2AB(g)⇔A2(g)+B2(g)
The vapour density of the equilibrium mixture does not depend upon
View SolutionConsider the following hypothetical equilibrium
2B(g)⇔B2(g)
If d is observed vapour density and D is theoretical vapour density, then degree of association (α) will be
View Solution
