Let Z be the set of integers. If A = ${x \in Z : 2 (x + 2) (x^{2} - 5 x + 6)} = 1$ and $B = {x \in Z : - 3 < 2 x - 1 < 9}$ , then the number of subsets of the set A $\times$ B is

$2^{18}$

$2^{12}$

$2^{15}$

$2^{10}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

If $- 5 < 2 x - 3 \leq x + 2, x \in R$ , then the solution set of x on the number line is
A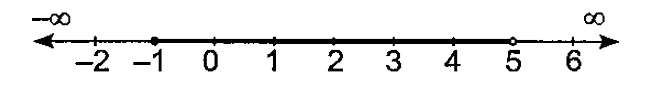
B
C
D
If $2 x - 3 < x + 1 < 4 x + 7, x \in R$ then the solution set of x on the number line is:
A
B
C
D
If $2 x - 5 \leq 5 x + 4 < 29$ and x is an integer, then the solution set of x is
A ${- 2, - 1, 0, 1, 2, 3, 4, 5}$
B ${- 2, - 1, 0, 1, 2, 3, 4}$
C ${- 3, - 2, - 1, 0, 1, 2, 3, 4, 5}$
D ${- 3, - 2, - 1, 0, 1, 2, 3, 4}$