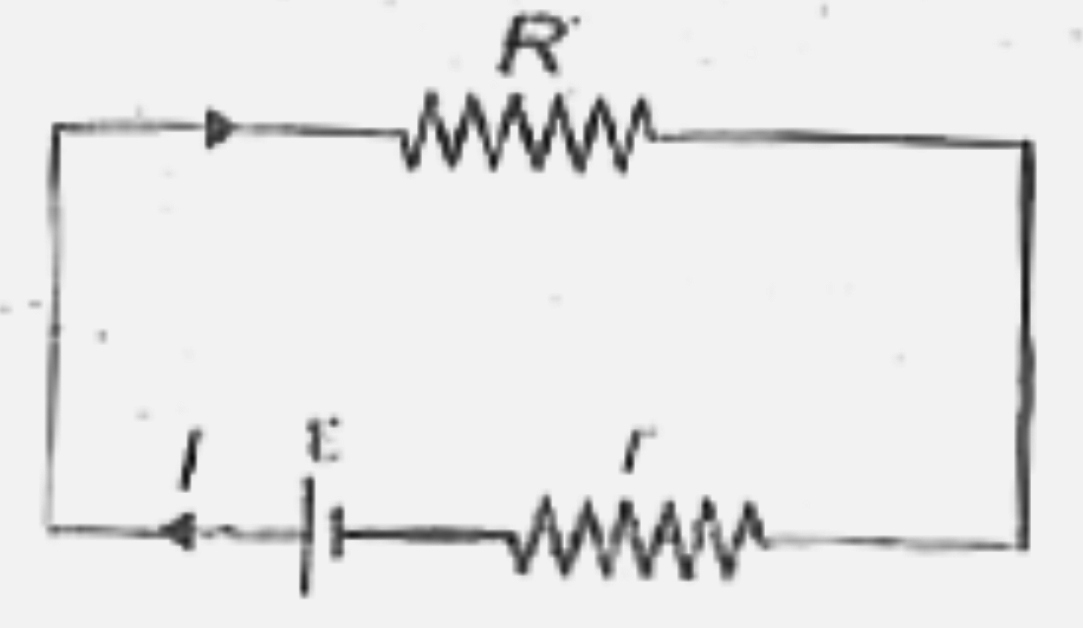
A cell of emf ε and internal resistance r drives a current i through an extermal resistance R
(i) The cell suppllied εi power
(ii) Heat is produced in R at the rate εi
(iii) Heat is produced in R at the rate εI(RR+r)
(iv) Heat is produced in the cell at the rate εi(rR+r)
The correct Answer is:A, C, D
To solve the problem, we need to analyze the power supplied by the cell, the heat produced in the external resistance R, and the heat produced in the internal resistance r of the cell.
1. Power Supplied by the Cell:
The power supplied by the cell can be expressed as:
Psupplied=ϵi
where ϵ is the EMF of the cell and i is the current flowing through the circuit.
Hint: Remember that the total power supplied by the cell is the product of EMF and the current.
2. Power Dissipated in the External Resistance R:
The heat produced in the external resistance R is given by Joule's law:
PR=i2R
This represents the rate of heat produced in the resistor due to the current flowing through it.
Hint: Use the formula P=I2R to find the power dissipated in the resistor.
3. Power Dissipated in the Internal Resistance r:
The power dissipated in the internal resistance of the cell is:
Pr=i2r
This is the heat produced in the internal resistance due to the current flowing through it.
Hint: Similar to the external resistance, apply P=I2R for the internal resistance as well.
4. Total Power Supplied:
The total power supplied by the cell is used to overcome both the external and internal resistances:
Ptotal=PR+Pr=i2R+i2r=i2(R+r)
Thus, we can express the current i in terms of ϵ and the resistances:
i=ϵR+r
Hint: The total power supplied by the cell equals the sum of the power dissipated in both resistances.
5. Heat Produced in the External Resistance R:
Substituting i in the expression for PR:
PR=i2R=(ϵR+r)2R=ϵ2R(R+r)2
Hint: Substitute the expression for current i into the power formula for the external resistance.
6. Heat Produced in the Internal Resistance r:
Similarly, substituting i in the expression for Pr:
Pr=i2r=(ϵR+r)2r=ϵ2r(R+r)2
Hint: Again, substitute the expression for current i into the power formula for the internal resistance.
Conclusion:
From our analysis, we can conclude that:
- The power supplied by the cell is ϵi.
- The heat produced in the external resistance R is ϵ2R(R+r)2.
- The heat produced in the internal resistance r is ϵ2r(R+r)2.
Thus, the correct options based on the statements provided in the question are:
- (iii) Heat is produced in R at the rate ϵiRR+r.
- (iv) Heat is produced in the cell at the rate ϵirR+r.
The power supplied by the cell can be expressed as:
Psupplied=ϵi
where ϵ is the EMF of the cell and i is the current flowing through the circuit.
The heat produced in the external resistance R is given by Joule's law:
PR=i2R
This represents the rate of heat produced in the resistor due to the current flowing through it.
The power dissipated in the internal resistance of the cell is:
Pr=i2r
This is the heat produced in the internal resistance due to the current flowing through it.
The total power supplied by the cell is used to overcome both the external and internal resistances:
Ptotal=PR+Pr=i2R+i2r=i2(R+r)
Thus, we can express the current i in terms of ϵ and the resistances:
i=ϵR+r
Substituting i in the expression for PR:
PR=i2R=(ϵR+r)2R=ϵ2R(R+r)2
Similarly, substituting i in the expression for Pr:
Pr=i2r=(ϵR+r)2r=ϵ2r(R+r)2
From our analysis, we can conclude that:
- The power supplied by the cell is ϵi.
- The heat produced in the external resistance R is ϵ2R(R+r)2.
- The heat produced in the internal resistance r is ϵ2r(R+r)2.
- (iii) Heat is produced in R at the rate ϵiRR+r.
- (iv) Heat is produced in the cell at the rate ϵirR+r.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-4)
12 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-1)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-2)
16 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Video
Similar Questions
A cell of emf ε and internal resistance r is charged by a current I, then
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
View SolutionA battery of ε and internal resistance r is used in a circuit with a variable external resistance R. Find the value of R for which the power consumed in R is maximum.
View SolutionA cell of emf 'E' and internal resistance 'r' draws a current 'I'. Write the relation between terminal voltage 'V' in terms of E, I and r.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
View SolutionA cell to emf. E and internal resistance r supplies currents for the same time t through external resistanceR1andR2 respectively. If the heat produced in both cases is the same, then the internal resistance is given by :
View Solution2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA battery of emf epsilon and internal resistance r is connected across a load resistance RL . The plot between output power and load resistance is shown in the figure. The value of emf epsilon and internal resistance r respectively will
_PHY_E05_112_Q01.png)
View SolutionA cell supplies a current i1 trhough a resistnace R1 and a current i2 through a resistance R2. The internal resistance of this cell is
View Solution
