The following figure a conducting disc rotating about its axis in a perpendicular magnetic field B. The resistor of resistance R is connected between the centre and the rim. The current in the resistor is (The radius of the disc is 5.0 cn=m, angular speed ω=10rads−1,B=0.40TandR=10Ω)
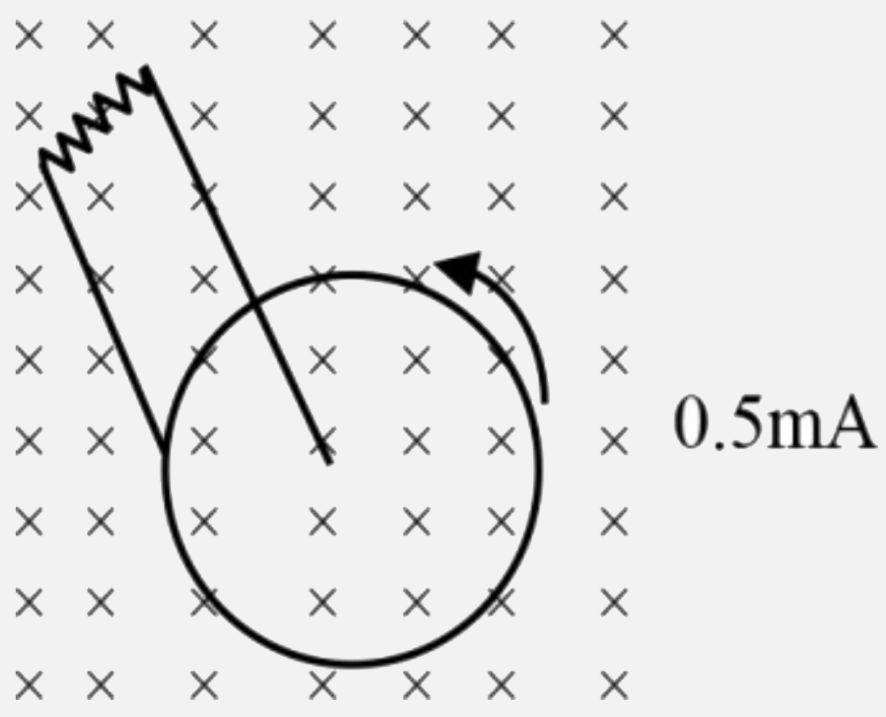
0.5 A
0.2 A
0.3 A
0.9 A
The correct Answer is:A
Step by step video & image solution for The following figure a conducting disc rotating about its axis in a perpendicular magnetic field B. The resistor of resistance R is connected between the centre and the rim. The current in the resistor is (The radius of the disc is 5.0 cn=m, angular speed omega=10 rad s^(-1) , B = 0.40 T and R = 10 Omega) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View Solution
Knowledge Check
Figure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed ω=40rad/s,B=0.10T and R=1Ω. The current through the resistor is
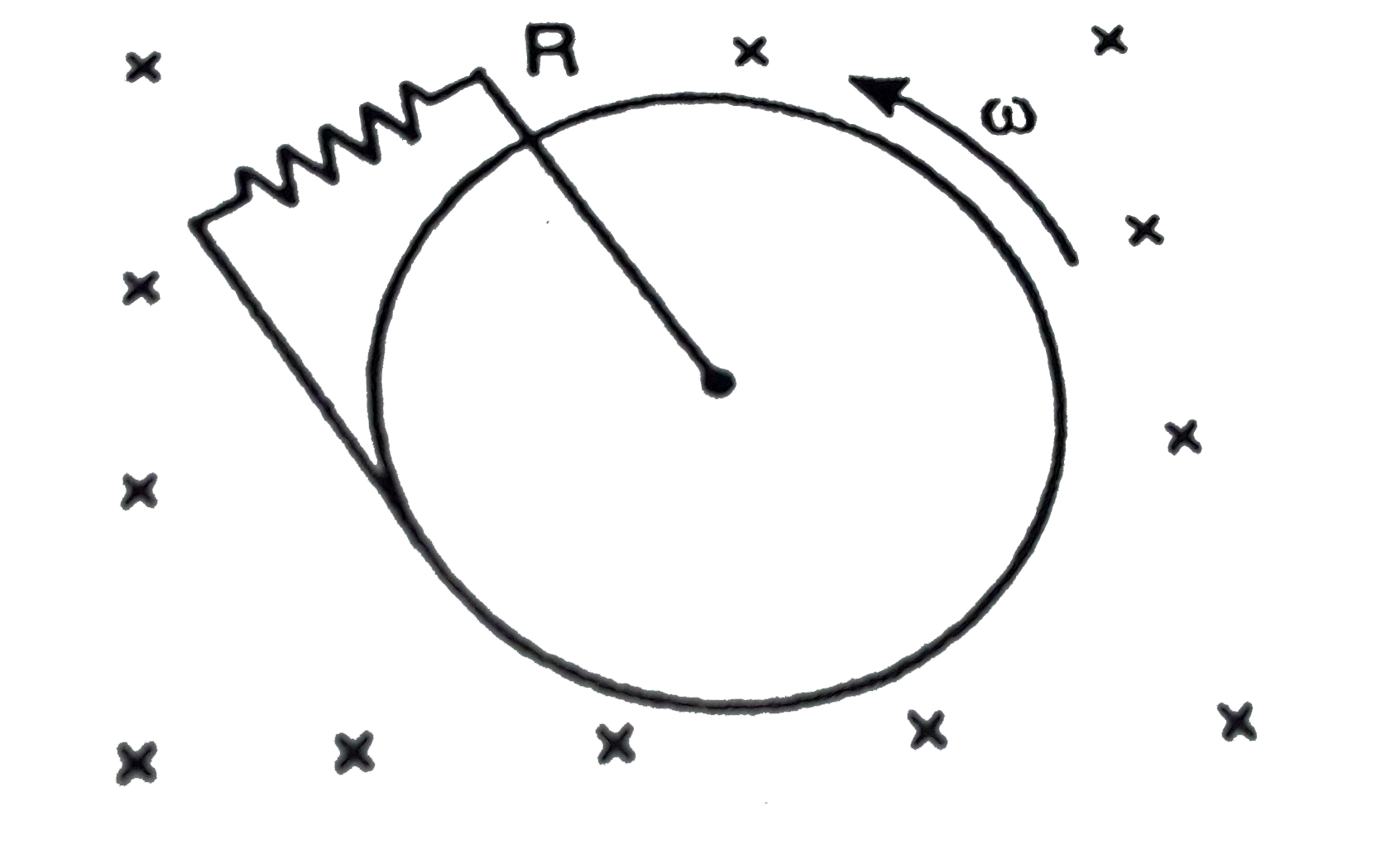 A5mAB50AC5AD10mA
A5mAB50AC5AD10mAA non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23a conducting disc of radius R roatates about its axis when an angular velocity ω.Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
AzeroBmeω2R22eCmeω2R23eDemeω2R22
A conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

View Solution
