Two point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
The correct Answer is:2540ˆi+2000ˆj+1720ˆkN/C
To find the electric field intensity at point C due to the two point charges located at points A and B, we will follow these steps:
Step 1: Identify the Charges and Their Positions
- Charge Q1=3μC=3×10−6C is located at point A (1, 1, 2) m.
- Charge Q2=2.5μC=2.5×10−6C is located at point B (0, 3, -1) m.
- We need to find the electric field at point C (3, 3, 3) m.
Step 2: Calculate the Position Vectors
- Position vector from A to C:
→rA=→C−→A=(3−1)^i+(3−1)^j+(3−2)^k=2^i+2^j+1^k
- Position vector from B to C:
→rB=→C−→B=(3−0)^i+(3−3)^j+(3−(−1))^k=3^i+0^j+4^k
Step 3: Calculate the Magnitudes of the Position Vectors
- Magnitude of →rA:
rA=√(2)2+(2)2+(1)2=√4+4+1=√9=3m
- Magnitude of →rB:
rB=√(3)2+(0)2+(4)2=√9+0+16=√25=5m
Step 4: Calculate the Electric Fields at Point C
- Electric field due to charge Q1 at point C:
→EA=kQ1r2A^rA
where k=9×109N⋅m2/C2 and ^rA is the unit vector in the direction of →rA:
^rA=→rArA=2^i+2^j+1^k3
Thus,
→EA=9×109⋅3×10−632(23^i+23^j+13^k)
=9×109⋅3×10−69(23^i+23^j+13^k)
=103(2^i+2^j+1^k)=2000^i+2000^j+1000^kN/C
- Electric field due to charge Q2 at point C:
→EB=kQ2r2B^rB
where ^rB is the unit vector in the direction of →rB:
^rB=→rBrB=3^i+0^j+4^k5
Thus,
→EB=9×109⋅2.5×10−652(35^i+0^j+45^k)
=9×109⋅2.5×10−625(35^i+0^j+45^k)
=103⋅(0.3^i+0+0.4^k)=720^i+0^j+720^kN/C
Step 5: Calculate the Resultant Electric Field at Point C
- Adding the electric fields →EA and →EB:
→Enet=→EA+→EB=(2000+720)^i+(2000+0)^j+(1000+720)^k
=2720^i+2000^j+1720^kN/C
Final Result
The electric field intensity at point C is:
→Enet=2720^i+2000^j+1720^kN/C
- Charge Q1=3μC=3×10−6C is located at point A (1, 1, 2) m.
- Charge Q2=2.5μC=2.5×10−6C is located at point B (0, 3, -1) m.
- We need to find the electric field at point C (3, 3, 3) m.
- Position vector from A to C:
→rA=→C−→A=(3−1)^i+(3−1)^j+(3−2)^k=2^i+2^j+1^k
- Position vector from B to C:
→rB=→C−→B=(3−0)^i+(3−3)^j+(3−(−1))^k=3^i+0^j+4^k
- Magnitude of →rA:
rA=√(2)2+(2)2+(1)2=√4+4+1=√9=3m
rB=√(3)2+(0)2+(4)2=√9+0+16=√25=5m
- Electric field due to charge Q1 at point C:
→EA=kQ1r2A^rA
where k=9×109N⋅m2/C2 and ^rA is the unit vector in the direction of →rA:
^rA=→rArA=2^i+2^j+1^k3
Thus,
→EA=9×109⋅3×10−632(23^i+23^j+13^k)
=9×109⋅3×10−69(23^i+23^j+13^k)
=103(2^i+2^j+1^k)=2000^i+2000^j+1000^kN/C
→EB=kQ2r2B^rB
where ^rB is the unit vector in the direction of →rB:
^rB=→rBrB=3^i+0^j+4^k5
Thus,
→EB=9×109⋅2.5×10−652(35^i+0^j+45^k)
=9×109⋅2.5×10−625(35^i+0^j+45^k)
=103⋅(0.3^i+0+0.4^k)=720^i+0^j+720^kN/C
- Adding the electric fields →EA and →EB:
→Enet=→EA+→EB=(2000+720)^i+(2000+0)^j+(1000+720)^k
=2720^i+2000^j+1720^kN/C
The electric field intensity at point C is:
→Enet=2720^i+2000^j+1720^kN/C
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (C)
Explore 14 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (D)
Explore 5 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Two point charges 2μC and −2μC are placed at point A and B as shown in figure. Find out electric field intensity at points C and D. [All the distances are measured in meter].

View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).

View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View SolutionTwo point charges q1(√10μC) and q2(−25μC) are placed on the x-axis at x = 1 m and x = 4 m respectively. The electric field (in V/m) at a point y =3 m on y-axis is,
[take 14π∈0=9×109Nm2C−2]
View SolutionTwo point charges q1=20μC and q2=25μC are placed at (-1, 1, 1) m and (3, 1, -2)m, with respect to a coordinate system. Find the magnitude and unit vector along electrostatic force on q2 ?
View SolutionTwo charges of −4μCand+4μC are placed at the points A(1,0,4)andB(2,−1,5) location in an electric field →E=0.20ˆiV/cm. Calculate the torque acting on the dipole.
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric. field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
View SolutionTwo point charges of 5μC and 20μC are separated by a distance of 2m. Find the point on the line joining them at which electric field intensity is zero.
View Solution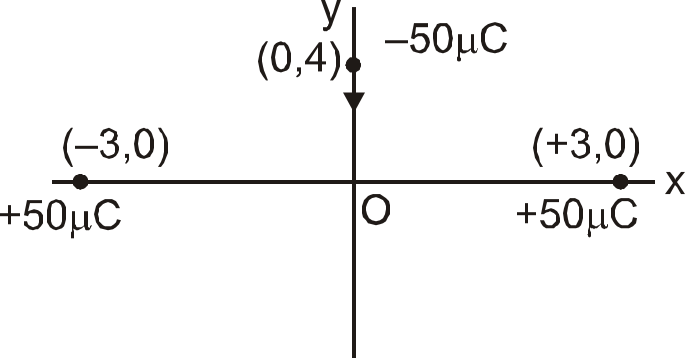
The figure shows two equal, positive charges, each of magnitude50μC, fixed at points (3, 0) m and (–3, 0)m respectively. A charge –50μC, moving along negative y–axis has a kinetic energy of 4J at the instant it crosses point (0,4)m. Determine the position of this charge where the direction of its motion reverses for the first time after crossing this point (neglect gravity).
View Solution
