A uniform electric field of 20 N/C exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 40 cm.
8 VOLTS
-8 VOLTS
0 VOLTS
NONE OF THESE
The correct Answer is:A
To solve the problem of finding the increase in electric potential as one moves up through a height of 40 cm in a uniform electric field of 20 N/C directed downward, we can follow these steps:
1. Identify the Given Values:
- Electric field E=20N/C (downward).
- Height h=40cm=0.40m.
2. Understand the Relationship Between Electric Field and Electric Potential:
- The relationship between electric field E and electric potential V is given by:
E=−dVdr
- This implies that the change in electric potential ΔV can be expressed as:
ΔV=−E⋅Δr
- Here, Δr is the displacement in the direction of the field.
3. Determine the Direction of Displacement:
- Since the electric field is directed downward, moving upward (against the field) means that Δr will be positive in the upward direction. Therefore, we can consider Δr=+0.40m.
4. Calculate the Change in Electric Potential:
- Substitute the values into the equation:
ΔV=−E⋅Δr=−20N/C⋅0.40m
- Performing the multiplication:
ΔV=−20⋅0.40=−8V
5. Interpret the Result:
- The negative sign indicates that the potential decreases as one moves upward against the electric field. However, since the question asks for the increase in potential, we take the absolute value:
Increase in Electric Potential=8V
Final Answer:
The increase in electric potential as one goes up through a height of 40 cm is 8 volts.
---
- Electric field E=20N/C (downward).
- Height h=40cm=0.40m.
- The relationship between electric field E and electric potential V is given by:
E=−dVdr
- This implies that the change in electric potential ΔV can be expressed as:
ΔV=−E⋅Δr
- Here, Δr is the displacement in the direction of the field.
- Since the electric field is directed downward, moving upward (against the field) means that Δr will be positive in the upward direction. Therefore, we can consider Δr=+0.40m.
- Substitute the values into the equation:
ΔV=−E⋅Δr=−20N/C⋅0.40m
- Performing the multiplication:
ΔV=−20⋅0.40=−8V
- The negative sign indicates that the potential decreases as one moves upward against the electric field. However, since the question asks for the increase in potential, we take the absolute value:
Increase in Electric Potential=8V
The increase in electric potential as one goes up through a height of 40 cm is 8 volts.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)9videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (B)12videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP40videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
Similar Questions
A Uniform electric field of 10NC−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50cm.
View SolutionA uniform magnetic field of 0.20×10−3T exists in the space. Find the the change in the magnetic scalar potential as one moves through 50cm along the field.
View SolutionA uniform electric field E0 is directed along positive y-driection. Find the change in electric potential energy of a positive test charge q0 when it is displaced in this field from yi=a to yf=2a along the y-axis.
View SolutionA uniform electric field E0 is directed along positive y-driection. Find the change in electric potential energy of a positive test charge q0 when it is displaced in this field from yi=a to yf=2a along the y-axis.
View SolutionA uniform electric field of magnitude E=100NC−1 exists in the space in x-direction. Calculate the flux of this field through a plane square of edga 10 cm placed in the y-z plane. Take the normal along the positive x-axis to be positive.
View SolutionA particle of mass an charge q is projected vertically upwards .A uniform electric field →E is acted vertically downwards.The most appropriate graph between potential energy U (gravitation plus electrostatic) and height h(<< radius of earth) is :(assume U to be zero on surface of earth)
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30∘ with x-axis .
Then
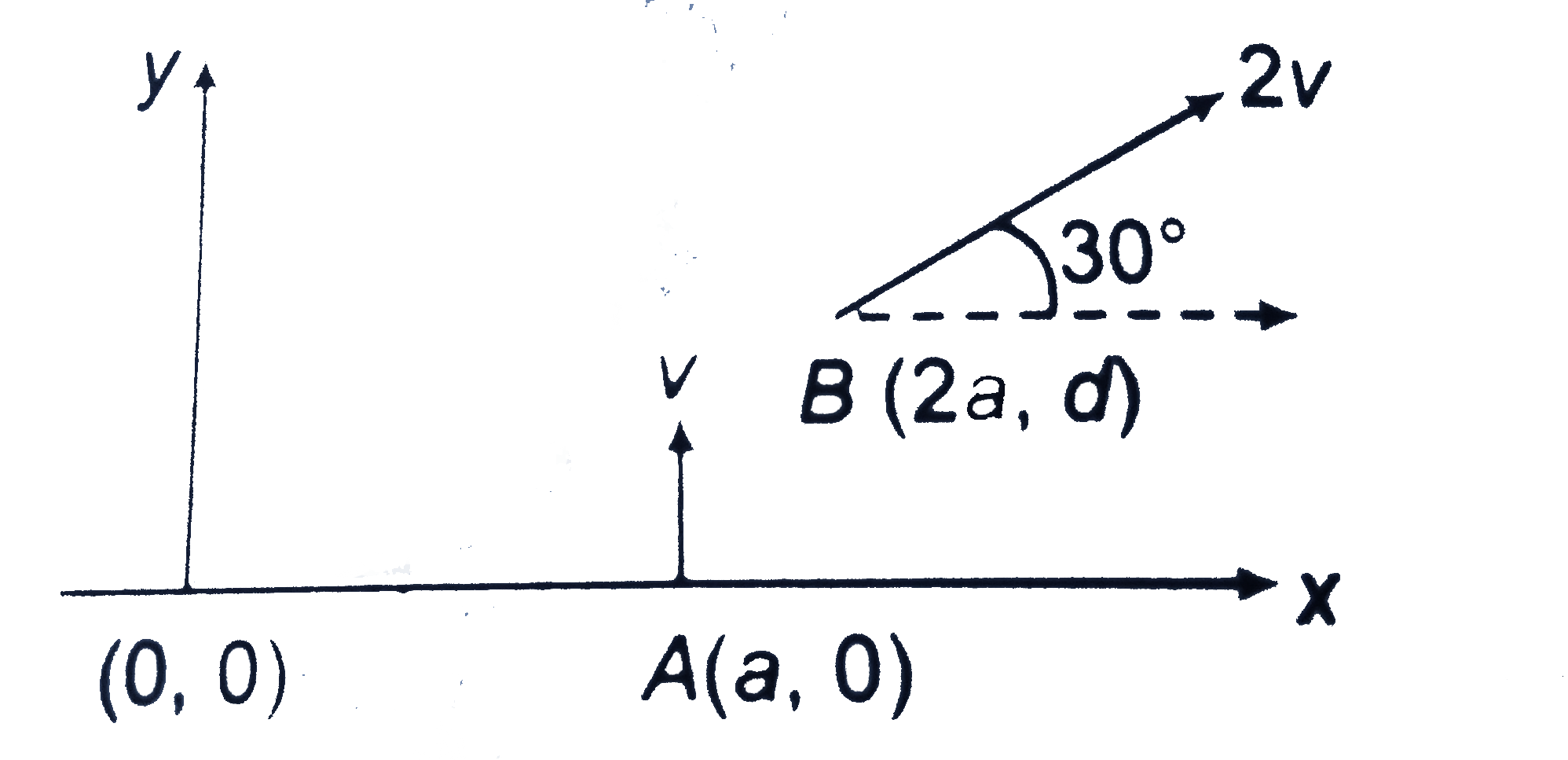View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.
View Solution(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(b) Derive an expression for the electric potential at any point along the axial line of an electric dipoleView SolutionAn electron is moving along +x direction with a velocity of 6×106ms−1 . It enters a region of uniform electric field of 300 V/cm pointing along + y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x direction will be :
View Solution