If E=2r2 then find V(r)
To find the electric potential V(r) given the electric field E=2r2, we can follow these steps:
Step 1: Understand the relationship between electric field and potential
The electric field E is related to the electric potential V by the equation:
E=−dVdr
This means that the electric field is the negative gradient of the electric potential.
Step 2: Set up the equation
Given that E=2r2, we can write:
−dVdr=2r2
Step 3: Rearrange the equation
Rearranging the equation gives us:
dVdr=−2r2
Step 4: Integrate both sides
To find V(r), we integrate both sides with respect to r:
V(r)=−∫2r2dr
Step 5: Perform the integration
The integral of 2r2 is:
∫2r2dr=23r3
Thus, we have:
V(r)=−23r3+C
where C is the constant of integration.
Step 6: Write the final expression
The final expression for the electric potential V(r) is:
V(r)=−23r3+C
Summary
The electric potential V(r) corresponding to the electric field E=2r2 is:
V(r)=−23r3+C
The electric field E is related to the electric potential V by the equation:
E=−dVdr
This means that the electric field is the negative gradient of the electric potential.
Given that E=2r2, we can write:
−dVdr=2r2
Rearranging the equation gives us:
dVdr=−2r2
To find V(r), we integrate both sides with respect to r:
V(r)=−∫2r2dr
The integral of 2r2 is:
∫2r2dr=23r3
Thus, we have:
V(r)=−23r3+C
where C is the constant of integration.
The final expression for the electric potential V(r) is:
V(r)=−23r3+C
The electric potential V(r) corresponding to the electric field E=2r2 is:
V(r)=−23r3+C
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (B)
Explore 12 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:HLP
Explore 40 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
If V=2r2 then find (i) →E(1,0,−2) (ii) →E(r=2)
View SolutionIf Tr=r(r2−1), then find ∞∑r=21T.
View SolutionR→R be defined by f(x)=(e2x−e−2x)2. is f(x) invertible. If yes then find f−1(x)
View SolutionR→R be defined by f(x)=(e2x−e−2x)2. is f(x) invertible. If yes then find f−1(x)
View SolutionIf x2+y2=R2(whereR>0)andk=y''(1+y'2)3 then find k in terms of R alone.
View SolutionIn a triangle ABC, if r1+r3+r=r2, then find the value of (sec2A+csc2B−cot2C),
View SolutionIf f:R→Randg:R→R are two mappings such that f(x)=2xandg(x)=x2+2 then find fogandgog.
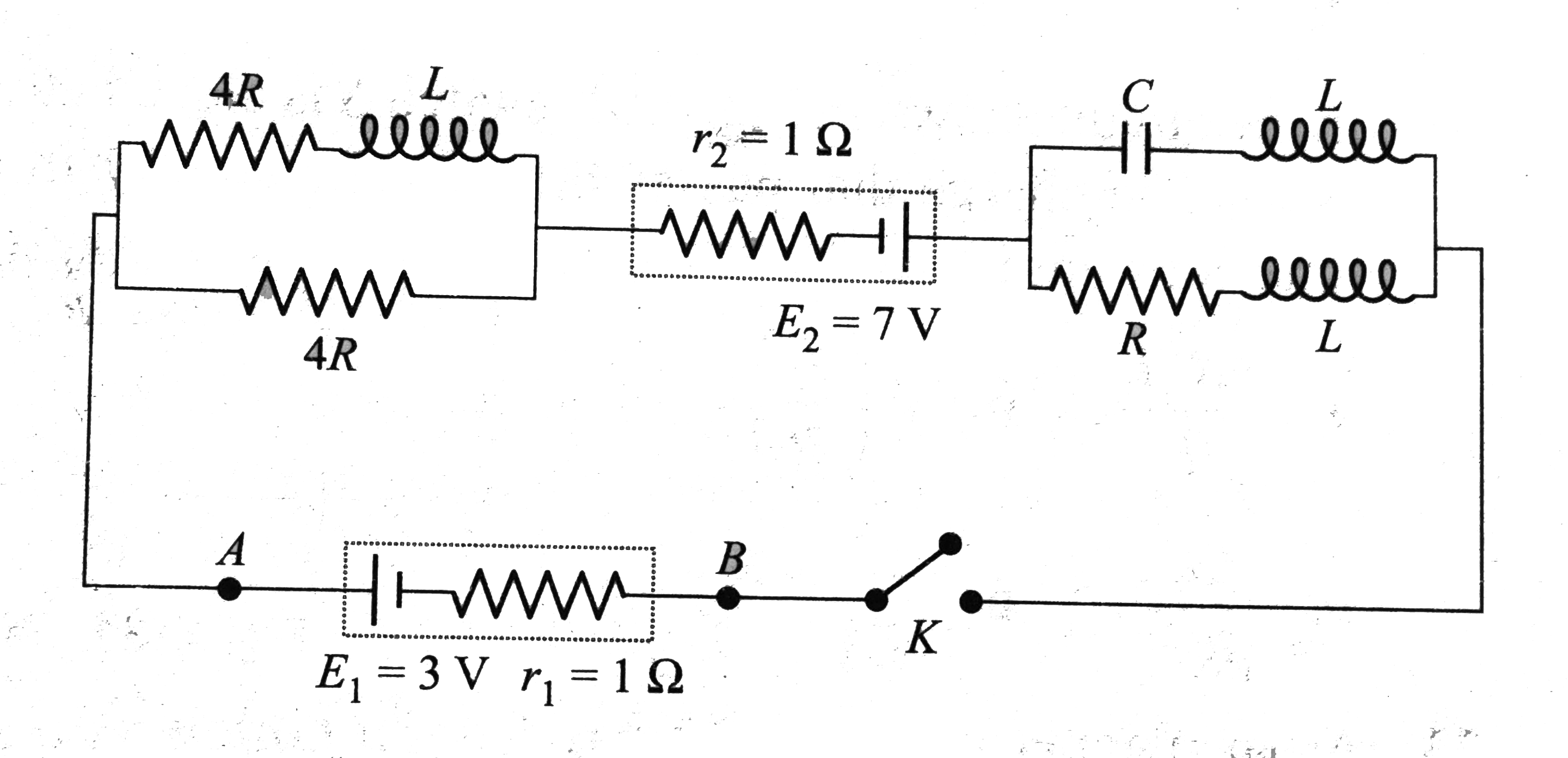
View SolutionIn Fig. key K is closed at t=0. After a long time, the potential difference between A and B is zero, the value of R will be [r1=r2=1Ω,E1=3V and E2=7V, C=2μF, L=4mH, where r1 and r2 are the internal resistances of cells E1 and E2, respectively].
View SolutionAssertion : The average velocity of a particle having initial and final velocity v1 and v2 is v1+v2/2.
Reason : If r1 and r2 be the initial and final displacement in time t, then vav=r1−r2t .
View SolutionTwo planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
View Solution