A charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then

Video Solution

Text Solution

Verified by Experts

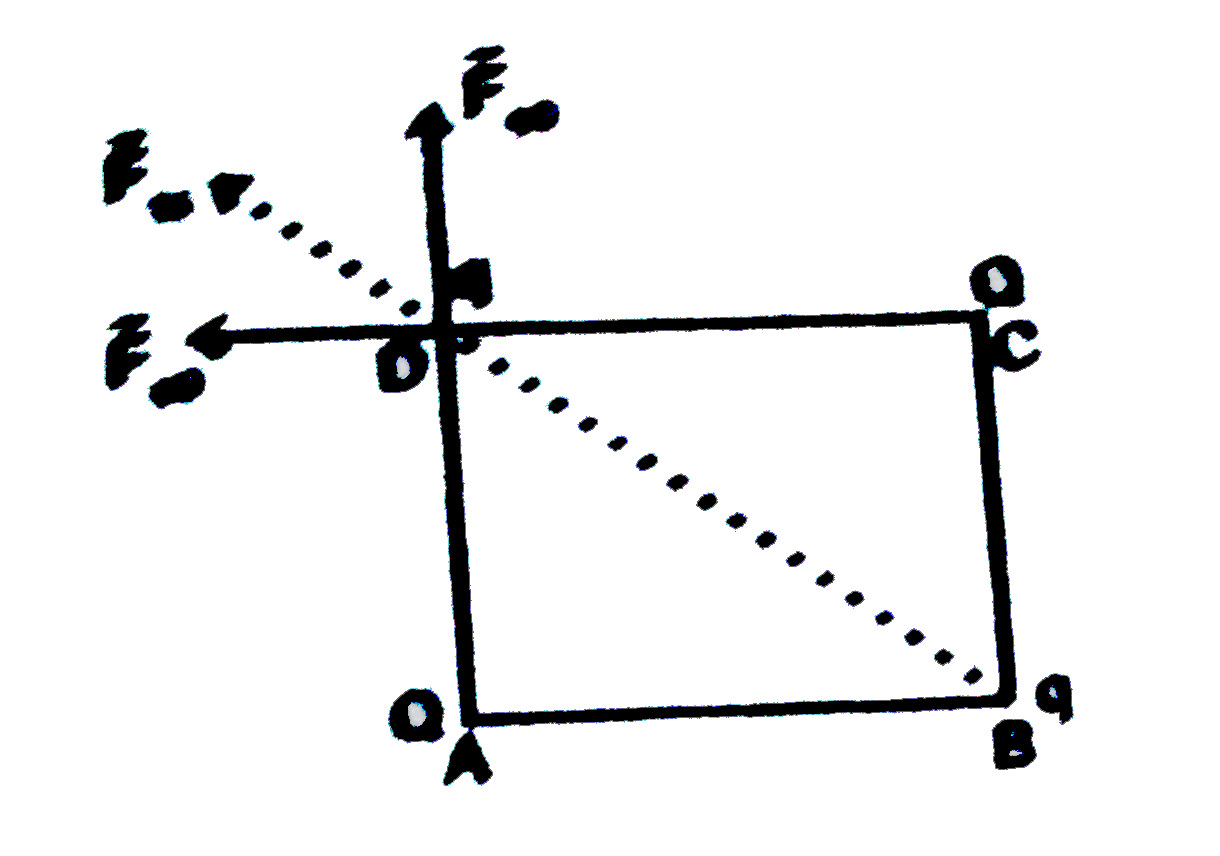
(a) Let on a square ABCD, charges are placed as shown

Now, forces on charge Q (at point A) due to other charge are ${\to F}_{Q Q}, {\to D}_{Q q}$ and ${\to F}_{Q q}$ respectively as shown in figure.
$F_{net}$ on $Q = {\to F}_{Q . Q} + {\to F}_{Q q} + {\to F}_{Q q}$ (at point A)
But $F_{net} = 0$
So, $Σ F_{x} = 0$
$Σ F_{x} = - F_{Q Q} {cos 45}^{\circ} - F_{Q q}$
$\Rightarrow \frac{K Q^{2}}{{(\sqrt{2} a)}^{2}} . \frac{1}{\sqrt{2}} + \frac{K Q q}{a^{2}} = 0 \Rightarrow q = - \frac{Q}{2 \sqrt{2}}$
(b) For resultant force on each charge o be zero :
From previous data, force on charge Q is zero when $q = - \frac{Q}{2 \sqrt{2}}$ If for this value of charge q, force on q is zero, then and only then the value of q exists for which the resultant force on each charge is zero.
Force on q :
Forces on charge q (at point D) due to other three charges are ${\to F}_{q Q}, {\to F}_{q q}$ and ${\to F}_{q Q}$ respectively as shown in figure.
Net force on charge q :
$- \to net = {\to F}_{q q} + {\to F}_{q Q} + {\to F}_{q Q}$ But ${\to F}_{net} = 0$
So, $Σ F_{x} = 0$
$Σ F_{x} = - \frac{K q^{2}}{{(\sqrt{2} a)}^{2}} . \frac{1}{\sqrt{2}} - \frac{K Q q}{{(a)}^{2}} \Rightarrow q = 2 \sqrt{2} - Q$
But from previous condition, $q = - \frac{Q}{2 \sqrt{2}}$
So, no value of q makes the resultant force on each charge zero.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-ELECTROSTATICS-Problems

Home
Ask Doubt
Profile