Two identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
The correct Answer is:103 m/s
To solve the problem, we will use the principle of conservation of mechanical energy. The initial potential energy of the charged particle will convert into kinetic energy as it moves closer to the two fixed charges.
1. Identify the Charges and Distances:
- The two identical charges, Q1=Q2=5μC=5×10−6C, are fixed at a distance of 8cm=0.08m apart.
- The charged particle, q=−10μC=−10×10−6C, is placed 5cm=0.05m from each charge initially.
2. Determine the Final Position:
- When the particle is released and moves towards the two charges, it will be at the midpoint between them when it is nearest to both charges. The distance from each charge to the midpoint is 4cm=0.04m.
3. Calculate Initial and Final Potential Energy:
- The initial potential energy Ui when the particle is at 5cm from each charge:
Ui=k(Q1⋅qr1+Q2⋅qr2)=k(5×10−6⋅(−10×10−6)0.05+5×10−6⋅(−10×10−6)0.05)
Ui=2⋅k(−50×10−120.05)=2⋅k⋅(−1×10−9)=−2k×10−9
- The final potential energy Uf when the particle is at 4cm from each charge:
Uf=k(Q1⋅qr′1+Q2⋅qr′2)=k(5×10−6⋅(−10×10−6)0.04+5×10−6⋅(−10×10−6)0.04)
Uf=2⋅k(−50×10−120.04)=2⋅k⋅(−1.25×10−9)=−2.5k×10−9
4. Apply Conservation of Energy:
- According to the conservation of mechanical energy:
Ki+Ui=Kf+Uf
- Initially, the kinetic energy Ki=0 (since the particle is released from rest), so:
0+Ui=Kf+Uf
- Rearranging gives:
Kf=Ui−Uf
- Substituting the values:
Kf=(−2k×10−9)−(−2.5k×10−9)=0.5k×10−9
5. Calculate the Kinetic Energy:
- The kinetic energy Kf can also be expressed as:
Kf=12mv2
- Setting the two expressions for kinetic energy equal:
12mv2=0.5k×10−9
- Solving for v2:
v2=k×10−9m
6. Substituting Values:
- Using k=9×109N⋅m2/C2 and m=9×10−6kg:
v2=9×109×10−99×10−6=103
- Therefore, v=√103=101.5=31.62m/s.
Final Answer:
The speed of the particle when it is nearest to the two charges is approximately 31.62m/s.
- The two identical charges, Q1=Q2=5μC=5×10−6C, are fixed at a distance of 8cm=0.08m apart.
- The charged particle, q=−10μC=−10×10−6C, is placed 5cm=0.05m from each charge initially.
- When the particle is released and moves towards the two charges, it will be at the midpoint between them when it is nearest to both charges. The distance from each charge to the midpoint is 4cm=0.04m.
- The initial potential energy Ui when the particle is at 5cm from each charge:
Ui=k(Q1⋅qr1+Q2⋅qr2)=k(5×10−6⋅(−10×10−6)0.05+5×10−6⋅(−10×10−6)0.05)
Ui=2⋅k(−50×10−120.05)=2⋅k⋅(−1×10−9)=−2k×10−9
Uf=k(Q1⋅qr′1+Q2⋅qr′2)=k(5×10−6⋅(−10×10−6)0.04+5×10−6⋅(−10×10−6)0.04)
Uf=2⋅k(−50×10−120.04)=2⋅k⋅(−1.25×10−9)=−2.5k×10−9
- According to the conservation of mechanical energy:
Ki+Ui=Kf+Uf
- Initially, the kinetic energy Ki=0 (since the particle is released from rest), so:
0+Ui=Kf+Uf
- Rearranging gives:
Kf=Ui−Uf
- Substituting the values:
Kf=(−2k×10−9)−(−2.5k×10−9)=0.5k×10−9
- The kinetic energy Kf can also be expressed as:
Kf=12mv2
- Setting the two expressions for kinetic energy equal:
12mv2=0.5k×10−9
- Solving for v2:
v2=k×10−9m
- Using k=9×109N⋅m2/C2 and m=9×10−6kg:
v2=9×109×10−99×10−6=103
- Therefore, v=√103=101.5=31.62m/s.
The speed of the particle when it is nearest to the two charges is approximately 31.62m/s.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (E)
2 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (F)
4 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (C)
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionTwo identical particles, each having a charge of 2.0×10−4C and mass of 10g, are kept at a separation of 10cm and then released. What would be the speeds of the particles when the separation becomes large?
View SolutionA point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
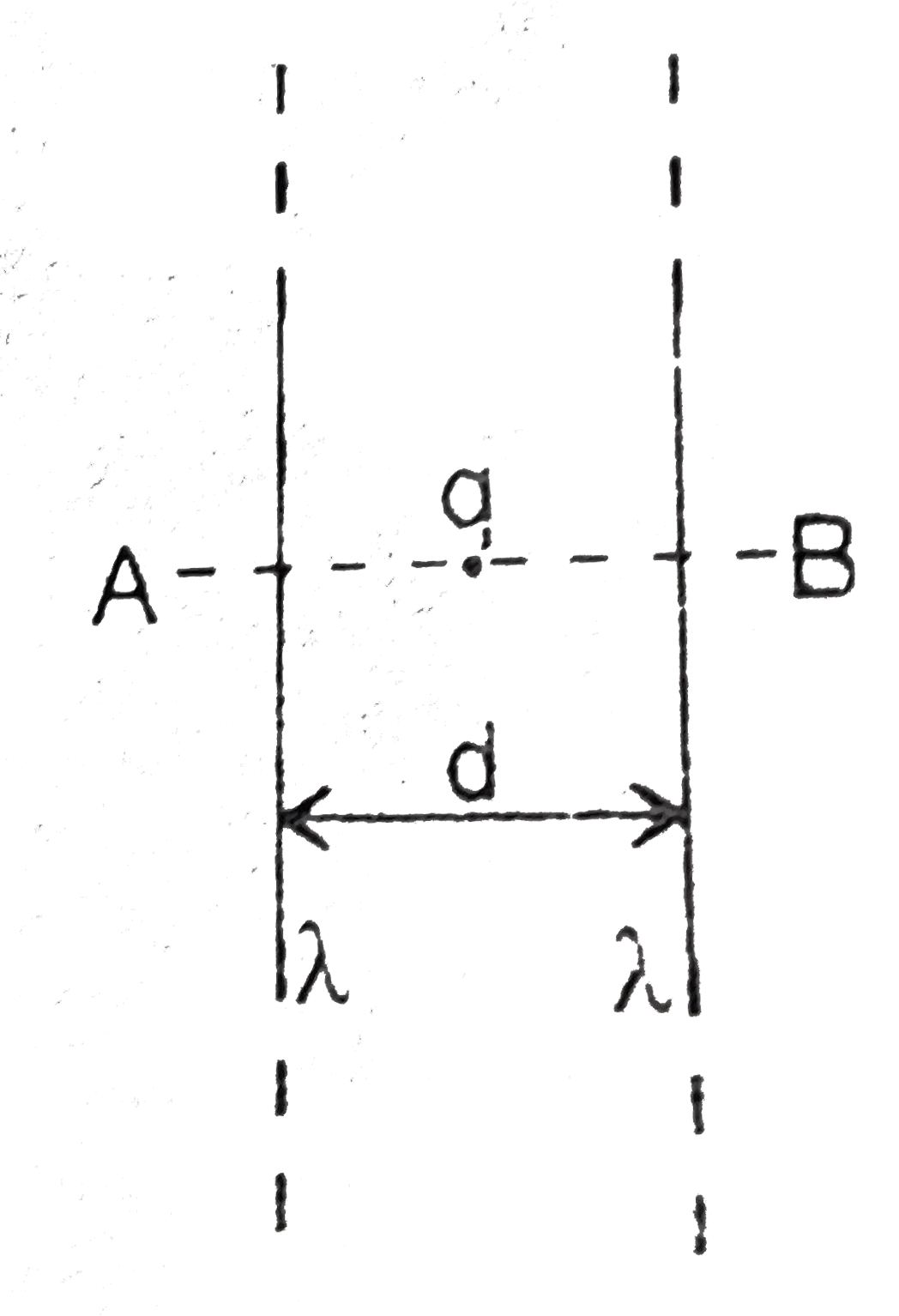
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionTwo charges 2μCand1μC are placed at a distance of 10cm. Where should a third charge be placed between them so that it does not experience any force.
View SolutionTwo positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation.
View SolutionTwo charges +10μC and +20μC are placed at a. separation of 2 cm. Find the electric potential due to the. pair at the middle point of the line joining the two charges.
View Solution
